
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод координат на плоскостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Совокупность координатных осей Ох, Оу (с выбранной единицей масштаба) и их точки пересечения (начало отсчета) называют декартовой прямоугольной (или кратко прямоугольной) системой координат. Каждой точке на плоскости соответствует одна пара действительных чисел х и у, которые называют координатами точки А (х; у). Координатные оси Ох и Оу разбивают плоскость на I, II, III и IVквадранты (координатные четверти).
Например, на рисунке 1 построены точки А (0; 4), В (3; 2), С (- 4; 0) М (-2;-3).
Основные задачи, решаемые методом координат Расстояние между двумя точками
Найдем расстояние между двумя точками М1 (х1;у1) и М2 (х2;у2) (рис. 2).
Из прямоугольного треугольника М1М2 N по теореме Пифагора находим формулу для вычисления расстояния между точками:
Пример. Найти расстояние между точками А (1; 3), В (4; 7). По формуле (7) имеем
Деление отрезка в данном отношении. Середина отрезка
Требуется найти координаты точки М (х;у), лежащую на отрезке М1М2 и делящую его в данном отношении
Еслиизвестны координаты концов отрезка М1 (х1;у1) и М2 (х2;у2), то координаты точки М(хМ;уМ), которая лежит на отрезке М1М2 и делит его в данном отношении
- координаты точки М(хМ;уМ) – середины отрезка М1М2
Пример. Вычислить координаты точки С – середины отрезка АВ, если А (1; 3), В (5; 7). По формулам (8) имеем
Ответ: С (3; 5). Пример. Вычислить координаты точки М, делящей отрезок АВ в отношении АМ: МВ =4, если А (10; 2), В (5; 7). По формулам (9) имеем
Ответ: М (6;6).
Упражнения
1. Построить точки A (3; 5), B (- 4; 2), C (1;-3), D (-2;-2), E (-6; 0). K (0; 3). 2. Найдите расстояние между точками: а) A (-3;-5) и B (2; 7); б) A (2; 7) и B (6; 4); в) A (12; 0) и B (0; -5); 3. Найдите координаты точки К – середины отрезка АВ: а) A (3; 7) и B (1; 7); б) A (5;-5) и B (5; 7); в) A (4; 3) и B (8; 1); г) A (-2; 4) и B (6; -7). 4. Найдите координаты точки М, которая делит отрезок АВ в отношении: а) 5. Найдите длины сторон треугольника с вершинами А (3; 2), В (-1; -1) и С (11; -6). 6. Доказать, что треугольник с вершинами О (0; 0), А (3; 1) и В (1; 7) прямоугольный. 7. Найти координаты вершин квадрата, диагональ которого равна 6 единицам длины, точка пересечения диагоналей – в начале координат, диагонали лежат на осях координат.
Уравнение прямой на плоскости
Общее уравнение прямой
В декартовой системе координат всякое уравнение первой степени относительно координат х и у Ах+Ву+С=0, (10) где А и В одновременно не равны нулю, определяет прямую в этой системе координат. Уравнение (10) называется общим уравнением прямой на плоскости, где Уравнение прямой, которая проходит через точку М (х0;у0)перпендикулярно вектору
Если прямая проходит через точку М (х0;у0)параллельно вектору
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.163 (0.007 с.) |




 . (7)
. (7)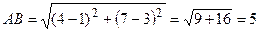 .
. (рис. 3).
(рис. 3).

 ; (8)
; (8) . (9)
. (9) .
.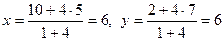 .
. , А (3; 5), В (9; 8); б)
, А (3; 5), В (9; 8); б)  , А (3; 5), В (9; 8); в)
, А (3; 5), В (9; 8); в)  , А (7; 11), В (2; 1); г)
, А (7; 11), В (2; 1); г)  , А (7; 11), В (2; 1).
, А (7; 11), В (2; 1). - нормальный (перпендикулярный) вектор данной прямой.
- нормальный (перпендикулярный) вектор данной прямой.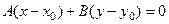 .
.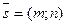 , то
, то .
.


