
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное расположение прямыхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Если две прямые лежат на плоскости, то возможны три случая их взаимного расположения: 1) пересекаются (т.е. имеют общую одну точку); 2) параллельны (не пересекаются и не совпадают); 3) совпадают. Прямые совпадают в случае, когда соответствующие коэффициенты в уравнениях прямых совпадают или пропорциональны.
Если прямые Условие параллельности прямых k 1= k 2 или Если прямые Ах1+Ву1+С1=0 и Ах2+Ву2+С2=0 пересекаются в некоторой точке М(х; у), то ее координаты удовлетворяют обоим уравнениям. Следовательно, чтобы найти координаты точки М, надо решить систему уравнений.
Прямые пересекаются, если имеют различные угловые коэффициенты.
Если прямые Условие перпендикулярности прямых
Пример. Написать уравнения прямых, проходящих через начало координат а) параллельно и б) перпендикулярно прямой у =2 x – 4. а) По формуле (18) k 1= k 2=2. Тогда по формуле (13) б) По формуле (19) Упражнения
1. Определите, какие из точек А (2; 0), В (7; 4) и С (3; 2) лежат на прямой у= 0,8 х- 1,6. 2. Напишите уравнение прямой, проходящей через точки А и В: а) А (2; 3), В (4; 5); б) А (4; -2), В (3; -4); в) А (3; 0), В (7; 4); г) А (3; 5), В (0; 4). 3. Напишите уравнение прямой у=kx+b: а) k= 3, b =2; б) k= -2, b = - 4; в) k= 4, b = - 5; г) k= 0, b =3; д) k= 4, b =0. 4. Записать уравнение прямой, проходящей через точку М и имеющей угловой коэффициент k: а) М (0; 2), k= 1; б) М (0; 0), k=- 1; в) М (0; -3), k= 0; г) М (0; 1), k= 0,5; 5. Построить прямые и записать общее уравнение прямой: а) 6. Напишите уравнение прямой в отрезках, если: а) а= 2, b =4; б) а= - 7, b =5; в) а= 6, b =-3; г) а= -5, b =-4. 7. Прямая проходит через точки А и В. Напишите уравнение прямой в отрезках: а) А (0; 2) и В (5; 0); б) А (-3; 0) и В (0;-2); в) А (0; 1) и В (-2; 0). 8. Напишите уравнение прямой в отрезках, найдите угловой коэффициент прямой, постройте эти прямые: а) 4 х – 6 у+ 12=0; б) 2 х + 3 у+ 12=0; в) - 2 х+ 5 у -10=0; г) 5 х+ 4 у - 20=0. 9. Параллельны ли прямые: а) б) в) 10. Перпендикулярны ли прямые: а) б) 11. Напишите уравнение прямой, которая проходит через точку М параллельно данной прямой: а) М (2;5), у= 4 х+ 3; б) М (-3;2), у=- 2 х+ 5; в) М (0;-3), у= 6 х - 5; г) М (4;0), у= 3. 12. Напишите уравнение прямой, которая проходит через точку М перпендикулярно данной прямой: а) М (4;3), у= 2 х+ 3; б) М (-5;1), у=- 2 х+ 7; в) М (2;- 5), у= 5 х +3; г) М (0;-5), у= 3. 13. Найдите тангенс угла между прямыми: а) 4 х– 6 у+ 2=0 и 2 х+ 4 у+ 5=0; б) 5 х– 3 у+ 8=0 и -5 х+ 8 у- 7=0; в) 4 х+ 2 у =0 и 4 у+ 5=0. 14. Найдите расстояние от точки К до прямой: а) 2 х+ 5 у+ 1=0, К (2;4); б) 3 х - 2 у - 5=0, К (-1;-2); в) - х+ 2 у+ 3=0, К (3;0). 15. Найти координаты точек пересечения прямой с осями: а) 16. Найдите координаты точки пересечения двух прямых: а) б) 17. Определите длины сторон треугольника, если даны уравнения прямых, содержащих его стороны:
КРИВЫЕ ВТОРОГО ПОРЯДКА
Кривыми второго порядка называются линии, уравнения которых могут быть записаны следующим образом:
К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
Уравнение окружности
Определение. Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром. Каноническое уравнение окружности
где Если центр окружности совпадает с началом координат, уравнение окружности имеет вид
Пример. Написать уравнение окружности радиуса R =3 с центром в точке С (1; 2). По формуле (20) имеем
Уравнение эллипса
Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F 1 и F 2(называемых фокусами эллипса) есть величина постоянная, равная 2 а. Если ось Ох проходит через фокусы F 1 и F 2 (расстояние между фокусами обозначим 2 с), а начало координат находится в середине отрезка F 1 F 2 (рис. 4), то фокусы имеют координаты F 1(-с; 0) и F 2(с; 0).
По определению и формуле (7) расстояния между точками получаем уравнение эллипса
Эллипс пересекает оси координат в четырех точках В результате преобразований получено каноническое уравнение эллипса
Эксцентриситетом эллипса ε называется отношение расстояния между фокусами к длине его большой оси. Если
Если
Если a=b, то уравнение (21) принимает вид Пример. Привести уравнение Разделим уравнение на 576 и приведем уравнение к каноническому виду Уравнение гиперболы
Определение. Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух данных точек F 1 и F 2(называемых фокусами гиперболы) есть величина постоянная, равная 2 а.
Если ось Ох проходит через фокусы F 1 и F 2 (расстояние между фокусами обозначим 2 с, причем По определению и формуле (7) расстояния между точками получаем уравнение гиперболы
Каноническое уравнение гиперболы имеет вид
где Если Если Если a=b, то гипербола называется равносторонней. Асимптотами служат взаимно перпендикулярные прямые Пример. Найти параметры (a, b, с, ε) гиперболы, заданной уравнением
Уравнение параболы
Определение. Параболой называется множество точек плоскости, равноудаленных от данной точки F (называемой фокусом параболы) и от данной прямой l (называемой директрисой параболы).
Каноническое уравнение параболы
Если уравнение содержит у 2, то график параболы симметричен относительно оси Ох; при p> 0 ветви параболы направлены вправо, при p< 0 – влево. Если уравнение содержит х 2, то ось параболы совпадает с осью Оу; при p> 0 ветви параболы направлены вверх, при p< 0 – вниз. Пример. Парабола с вершиной в начале координат проходит через точку А (9; 3) и симметрична относительно оси Ох. Написать каноническое уравнение. Подставляя координаты точки в уравнение (23), находим, что р =0,5 и Пример. Определить координаты фокуса, написать уравнение директрисы параболы у2= 36 х. Из формулы (23) находим р =18, следовательно фокус находится в точке F (9; 0), а х= - 18 – уравнение директрисы.
Упражнения
1. Написать уравнение окружности с радиусом R и центром в точке С: а) R= 5, С (2; 5); б) R= 2, С (-4; -1); в) R= 9, С (-8; 0); г) R= 12, С (0; -8). 2. Построить окружность: а) 3. Составить уравнение окружности, касающейся оси Ох и проходящей через точку А: а) А (2; 3); б) А (7; -1); в) А (-5; 4); г) А (0; -5). 4. Составить уравнение окружности, касающейся оси Оу и проходящей через точку А: а) А (5; 2); б) А (- 4; -2); в) А (3; 4); г) А (6; 0). 5. Написать уравнение окружности, проходящей через точку К, с центром в точке М: а) К (2; 3), М (0;2); б) К (- 4; -1), М (3; - 4); в) К (0; 5), М (0;0). 6. Написать каноническое уравнение эллипса, если даны его полуоси: а) а =3, b =5; б) а =4, b =2; в) а =1, b =7. 7. Какие из точек А (0; 2), В (3; 0), С (1; 2) лежат на эллипсе 8. Дан эллипс. Найдите длины осей, координаты вершин, расстояние между фокусами и эксцентриситет: а) 9. Написать уравнение эллипса, если известны координаты двух вершин: а) А 1(2; 0); В 1 (0; -3); б) А 2(-5; 0); В 2 (0; 2); в) А 1(6; 0); В 2 (0; 4). 10. Написать каноническое уравнение эллипса, определить длины полуосей, координаты вершин, расстояние между фокусами и эксцентриситет, постройте линию: а) 11. Написать каноническое уравнение гиперболы, если даны полуоси: а) a =3, b= 2; б) a =5, b= 4; в) a =5, b= 13; г) a =8, b= 10. 12. Напишите каноническое уравнение гиперболы. Найдите оси, координаты вершин, фокусов, расстояние между фокусами, уравнения асимптот и эксцентриситет гиперболы: а) 13. Написать уравнение гиперболы, если: а) ее фокусы находятся в точках F 1(-4; 0) и F 2(4; 0) и длина вещественной оси равна 6; б) ее фокусы находятся в точках F 1(0; -13) и F 2(0; 13) и длина мнимой оси равна 10. 14. Напишите уравнение равносторонней гиперболы, проходящей через точку К (3;-1). 15. Проверить, лежат ли точки А (2; -2) и В (1; 2) на параболе у2= 2 х. 16. Написать уравнение директрисы и найти координаты фокуса параболы: а) у2= 16 х; б) х2= -10 х; в) у2= - 4 х; г) х2= 12 у. 17. Написать уравнение параболы с вершиной в начале координат, для которых директрисами служат прямые: а) x= -2; б) x= 3; в) у= 4. .
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.011 с.) |

 .
. и
и 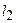 параллельны, то
параллельны, то  =
=  , следовательно k 1= k 2, т.е.параллельные прямые имеют равные угловые коэффициенты.
, следовательно k 1= k 2, т.е.параллельные прямые имеют равные угловые коэффициенты. (18)
(18)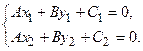
 , т.е.
, т.е.  .
.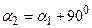 . Тогда
. Тогда  или
или 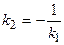 .
.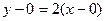 или. у =2 x.
или. у =2 x.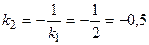 . Тогда
. Тогда  или у = –0,5 x.
или у = –0,5 x. ; б)
; б)  ; в)
; в) 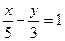 ; г)
; г) 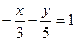 .
. и
и 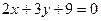 ;
;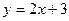 и
и 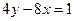 ;
;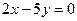 и
и 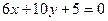 .
. и
и  ;
;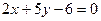 и
и  .
. ; б)
; б)  ; в)
; в) 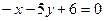 .
. и
и  ;
; и
и  .
.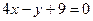 ,
,  и
и 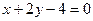 .
. .
. , (20)
, (20) - центр окружности; R – радиус окружности.
- центр окружности; R – радиус окружности. .
.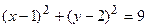 .
.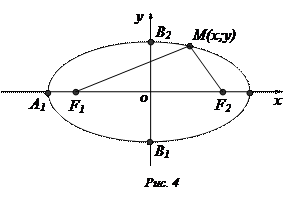
 .
.
 , которые называют вершинами эллипса Отрезок А 1 А 2 называется большой осью эллипса, а отрезок В 1 В 2 – его малой осью. Следовательно, а – длина большой полуоси эллипса, b – длина его малой полуоси.
, которые называют вершинами эллипса Отрезок А 1 А 2 называется большой осью эллипса, а отрезок В 1 В 2 – его малой осью. Следовательно, а – длина большой полуоси эллипса, b – длина его малой полуоси. . (21)
. (21)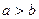 , то А 1 А 2 – большая ось, а В 1 В 2 – малая ось эллипса и
, то А 1 А 2 – большая ось, а В 1 В 2 – малая ось эллипса и и
и 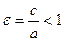 , F 1(- c; 0)и F 2(c; 0).
, F 1(- c; 0)и F 2(c; 0). , то А 1 А 2 – малая ось, а В 1 В 2 –большая ось эллипса и
, то А 1 А 2 – малая ось, а В 1 В 2 –большая ось эллипса и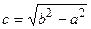 и
и 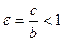 , F 1(0; - c)и F 2(0; c).
, F 1(0; - c)и F 2(0; c).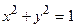 и определяет окружность с центром в начале координат. В этом случае с= 0.
и определяет окружность с центром в начале координат. В этом случае с= 0. к каноническому виду, определить параметры a, b, с и ε.
к каноническому виду, определить параметры a, b, с и ε.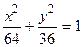 . Отсюда следует, что а= 8, b =6, с=
. Отсюда следует, что а= 8, b =6, с=  ,
, 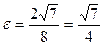 .
.
 ), а начало координат находится в середине отрезка F 1 F 2 (рис. 5), то фокусы имеют координаты F 1(-с; 0) и F 2(с; 0).
), а начало координат находится в середине отрезка F 1 F 2 (рис. 5), то фокусы имеют координаты F 1(-с; 0) и F 2(с; 0). .
. , (22)
, (22)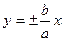 – асимптоты гиперболы (продолжение диагоналей прямоугольника 2a´2b);
– асимптоты гиперболы (продолжение диагоналей прямоугольника 2a´2b);  ;
; 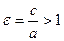 – эксцентриситет гиперболы
– эксцентриситет гиперболы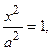 т.е. гипербола пересекает ось Ох в точках А 1(- а; 0) и А 2(а; 0), называемых вершинами гиперболы, отрезок А 1 А 2 – вещественная ось гиперболы, а – длина действительной полуоси, b – мнимой полуоси; F 1 (- c; 0) и F 2 (c; 0).
т.е. гипербола пересекает ось Ох в точках А 1(- а; 0) и А 2(а; 0), называемых вершинами гиперболы, отрезок А 1 А 2 – вещественная ось гиперболы, а – длина действительной полуоси, b – мнимой полуоси; F 1 (- c; 0) и F 2 (c; 0). , то при х=0 получают
, то при х=0 получают 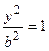 , т.е. гипербола пересекает ось Оу в точках В 1(0; - b) и B 2(0; b), отрезок B 1 B 2 – вещественная ось гиперболы, т.е. а – длина мнимой полуоси, b – действительной полуоси; F 1 (0; - c) и F 2 (0; c).
, т.е. гипербола пересекает ось Оу в точках В 1(0; - b) и B 2(0; b), отрезок B 1 B 2 – вещественная ось гиперболы, т.е. а – длина мнимой полуоси, b – действительной полуоси; F 1 (0; - c) и F 2 (0; c). .
.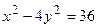 . Для этого приведем данное уравнение к каноническому виду
. Для этого приведем данное уравнение к каноническому виду 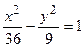 . Отсюда следует a =6, b =3, с=
. Отсюда следует a =6, b =3, с=  , ε =
, ε = 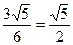 Уравнение асимптот гиперболы
Уравнение асимптот гиперболы 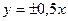 , фокусы F 1(-
, фокусы F 1(- 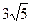 ; 0)и F 2(
; 0)и F 2(
 – фокус параболы;
– фокус параболы; 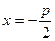 – уравнение директрисы.
– уравнение директрисы.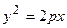 . (23)
. (23) . (24)
. (24) .
.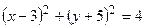 ; б)
; б) 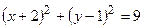 ; в)
; в) 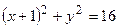 .
.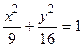 ?
? ; б)
; б) 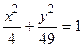 ; в)
; в) 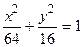 .
.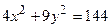 ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  .
.


