
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение обратной матрицы.Содержание книги Поиск на нашем сайте
Математика
Пермь УДК П
Рецензенты:
М Мусихина И.В. Математика: учебно-методическое пособие для студентов факультета физической подготовки. Часть 1– Пермь: ПГПУ, 2009. – 47 с.
Пособие содержит краткие теоретические сведения, упражнения и задания для самостоятельной решения по темам «Линейная алгебра» и «Аналитическая геометрия». Для студентов специальностей 032102.65 «Физическая культура для лиц с отклонениями в состоянии здоровья (Адаптивная физическая культура)», 100103 «Социально-культурный сервис и туризм» факультета физической подготовки Пермского государственного педагогического университета.
УДК …. ББК………
Печатается по решению редакционно-издательского отдела Пермского государственного педагогического университета.
ISBN?
© Пермский государственный педагогический университет, 2008 © Мусихина И.В., 2008
I. ЛИНЕЙНАЯ АЛГЕБРА
Матрицы и определители
Определение. Таблица чисел
состоящая из m строки n столбцов, называется матрицей размера m× n. Каждый элемент матрицы имеет двойной индекс: Если m≠n, то матрица прямоугольная. Если m= 1, n> 1, то рассматривают однострочную матрицу Если количество строк равно количеству столбцов (m=n), то матрицу называют квадратной. Число ее строк или столбцов называют порядком квадратной матрицы.
Например,
Матрица, в которой все элементы равны нулю, называется нулевой матрицей.
Например,
Матрица, в которой все элементы, кроме главной диагонали, равны нулю, называется диагональной. Диагональная матрица, все элементы которой равны 1, называется единичной
Например,
Две матрицы А и В называют равными (А=В), если они одинакового размера (т.е. имеют одинаковое число строк и одинаковое число столбцов) и их соответствующие элементы равны. Например, если
Порядком определителя называется число столбцов (строк) квадратной матрицы. Определение. Определитель второго порядка, соответствующий матрице
Пример. Определение. Определитель третьего порядка, соответствующий таблице элементов
Чтобы запомнить, какие произведения в правой части следует писать со знаком «+», какие – со знаком «-» применяют правило, называемое «правилом треугольника».
Пример. По формуле (2)
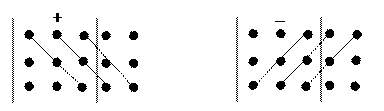
Иногда применяют следующую схему: справа приписывают два первых столбца, со знаком «+» берутся три произведения элементов, стоящих на главной и параллельной ей диагоналях, и со знаком «-» три произведения, стоящих на других диагоналях.
Минором Мik называется определитель (п-1)- го порядка, полученный из основного определителя, вычеркиванием i- той строки и k -того столбца. Так миноромданного элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент. Например, для элемента с2 определителя третьего порядка – это Алгебраическим дополнением данного элемента называется его минор, умноженный на (-1) т, где т – сумма номеров строки и столбца, содержащих данный элемент. Например, алгебраическое дополнениедля элемента с2 (вторая строка, третий столбец) определителя третьего порядка равно
Таким образом, знак, который при этом приписывается минору соответствующего элемента определителя, определяется следующей таблицей:
Определение. Определителем квадратной матрицы п- го порядканазывается число, равное сумме парных произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
∆=
Например, определитель третьего порядка равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения.
Пример.
Свойства определителя
1. Общий множитель какой-либо строки или столбца может быть вынесен за знак определителя.
Например,
2. Если все элементы одной строки (столбца) определителя соответственно равны нулю, то определитель равен нулю.
Например,
3. Если все элементы одной строки (столбца) определителя соответственно равны или пропорциональны элементам другой строки (столбца), то определитель равен нулю.
Например,
4. При перестановке двух строк (столбцов) знак определителя меняется на противоположный.
Например,
5. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. определитель не изменится, если его строки заменить столбцами, а столбцы – соответствующими строками (транспонировать).
Например, 6. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число (теорема о линейной комбинации). 7. Если в определителе какая-нибудь строка является линейной комбинацией остальных, то определитель равен нулю.
Вычисление определителей можно проводить путем последовательного понижения порядка определителя, используя его свойства. Пример. Выполним следующие преобразования: 1) по свойству (6) умножаем вторую строку на 5 и прибавляем ее к элементам первой строки; 2) умножаем вторую строку на 7 и прибавляем ее к элементам третьей строки; 3) расписываем определитель по элементам первого столбца.
Упражнения
Вычислить определитель второго порядка по определению 1) Вычислите определитель третьего порядка, разложив его по элементам 4) третьего столбца Вычислите определитель, используя свойства: 6) Вычислите определитель: 11) 15)
Действия над матрицами
1. Сложение матриц. Матрицы одинакового размера можно складывать. Определение. Суммой двух матриц одинакового размера А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.
Если
Пример. 1) 2) Законы сложения: А+В=В+А А+(В+С)=(А+В)+С А+О=А 2. Вычитание матриц. Вычитание определено для матриц одинакового размера. Определение. Разностью двух матриц одинакового размера А и В называется матрица С, элементы которой равны разности соответствующих элементов данных матриц.
Если
Пример. 1) 2)
Умножение матрицы на число. Определение. Произведением матрицы А на число λ называется матрица, элементы которой равны произведению числа λ на соответствующие элементыматрицы А.
При умножении матрицы на нуль получается нулевая матрица. Пример.
Сравните:
4. Умножение матрицы на вектор. Умножение определено, если число столбцов в матрице А равно числу элементов в векторе В. Определение. Результатом умножения матрицы А на одностолбцовую матрицу В будет матрица, каждый элемент которой является результатом перемножения соответствующей строки на элементы вектора В.
Пример.
5. Умножение матрицы на матрицу. Умножение определено в случае, если число столбцов первой матрицы равно числу строк второй. Определение. Произведением матрицы А на матрицу В называется матрица С, элементы которой имеют вид:
т.е. элемент таблицы С, стоящий в i -й строке и k -м столбце, равен сумме произведений соответствующих элементов i -й строки матрицы А и k -го столбца матрицы В. (m × n) (n × k) = (m × k)
Пример. 1) 2) 3) 4) Проверьте наоборот:
При умножении квадратных матриц особое значение имеют нулевая и единичная матрицы: Пример.
Свойства умножения матриц: А·В ≠ В·А 0·А = А·0 Е·А = А·Е Умножение матриц подчиняется сочетательному закону: А (ВС) = (АВ) С. Пример.
6. Возведение в степень. Так как возведение в степень сводится к умножению матрицы на себя, то это возможно только для квадратных матриц. Пример.
7. Транспонирование – замена строчек соответствующими столбцами. А =
Квадратная матрица и транспонированная к ней матрица имеют равные определители:
Упражнения
Выполните действия: 1) 3) 5) 7) 8) Найдите матрицу 2 А+ 5 В, если 9) Найдите матрицу 3 А -2 В, если Найдите произведение АВ и ВА, если 10) 11) 12) Найдите А 2, А 3, если 13) Найдите матрицу 2А2+3А+5Е, если 14) Определить ранг матрицы: а) А = Запишите транспонированную матрицу АТ к данной матрице А: 15) Найдите обратную матрицу к матрице А и проверьте выполнение равенства А·А-1=Е., если 17) 19)
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Равенство, содержащее неизвестную величину, называется уравнением. Значение неизвестной величины, при котором уравнение обращается в верное числовое равенство, называется корнем уравнения. Вид уравнения зависит от вида выражения. Вид целых уравнений определяется по степени старшего члена уравнения.
Например, 3 х +2=0 –линейное уравнение, а
Дана система т линейных уравнений с п неизвестными
Решением этой системы называется совокупность п чисел Коэффициенты системы линейных уравнений можно записать в виде таблицы, которая называется матрицей. Система уравнений называется совместной, если она имеет хотя бы одно решение. Если же система не имеет ни одного решения, то она называется несовместной. Совместная система называется определенной, если она имеет только одно решение, и неопределенной, если она имеет больше одного решения. Матрицы
называются соответственно матрицей и расширенной матрицей системы (3). Рассмотрим методы решения систем линейных уравнений с несколькими переменными.
Метод подстановки
Выражают одну переменную из какого-либо уравнения и подставляют в остальные уравнения. Так поступают до тех пор, пока не получат уравнение с одним неизвестным. Находят его значение, подставляют во все уравнения и находят значения других неизвестных.
Пример. Решить систему уравнений Выражаем переменную у из второго уравнения и подставляем в первое уравнение.
Ответ: (2; -1).
Формулы Крамера
Составим главный определитель системы (3), т.е. определитель матрицы А (4) из коэффициентов при неизвестных
и п вспомогательных определителей, полученных путем замены в главном определителе соответствующего столбца столбцом, состоящим из свободных членов:
Если
Пример. Решить систему
Ответ: Пример. Решить систему
х= Ответ: (1; 2; 3). Метод Гаусса Этот метод в школьном курсе математики известен как метод сложения. Суть его заключается в последовательном исключении неизвестных. Система уравнений при этом приводится к ступенчатому виду. Из преобразованной системы все неизвестные определяются последовательно.
Пример. Решить систему уравнений Умножаем второе уравнение на 6 и складываем его с первым, получим уравнение с одной переменной.
Ответ: (2; -1).
Если система имеет единственное решение, то ступенчатая система уравнений приводится к треугольной, в которой последнее уравнений содержит одно неизвестное.
Пример. Решить систему методом Гаусса
В качестве ведущего выберем 1-е уравнение системы, которое в дальнейшем останется без изменения. В качестве ведущего неизвестного – х, которое исключим из второго и третьего уравнения системы. Для этого из 1-го уравнения вычитаем второе, а затем 1-е уравнение умножаем на 3
В качестве ведущих возьмем второе уравнение и у. Исключим у из третьего уравнения, для этого второе уравнение умножаем на 2 (
Прямой ход метода Гаусса закончен. Обратным ходом получаем значения неизвестных:
Ответ: (4; 2; -1). В случае неопределенной системы, т.е. такой, в которой число неизвестных больше числа линейно независимых уравнений, некоторые неизвестные принимают за базисные, которые выражают через остальные (свободные).
Пример. Решить В данном случае число уравнений меньше числа неизвестных. Ранг системы r= 2. поэтому только два неизвестных будут базисными. Пусть неизвестные х и у – базисные, z – свободное. Выразим х и у через z
.
Придадим значение
Придавая t различные значения, будем получать различные частные решения данной системы уравнений. Ответ:
Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а соответствующую ей расширенную матрицу.
Пример. Решить систему уравнений Поменяем местами первое и второе уравнения.
Вычитаем из 2-й и 3-й строк 1-ю строку, умноженную соответственно на 3 и на 4; поменяем знаки во второй строке.
Умножаем 2-ю строку на 5 и прибавляем к 3-й строке. Далее разделим 3-ю строку на (-11)
Система уравнений приняла треугольный вид:
Она имеет единственное решение: Ответ: (2; 3; -1).
Матричный способ
Запишем систему уравнений (3) в матричной форме А Х=В, где А – матрица системы, Х – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Если определитель матрицы системы отличен от нуля (
АХ=В Þ А-1·АХ=А-1·В Х= А-1·В. (6) Пример.Решить матричным способом систему Для данной системы составим матрицы А= Найдем матрицу, обратную к матрице А А -1= Подставим ее в формулу (6)
т.е. Ответ: (2; -1; -3). Упражнения
Решите систему методом подстановки: 1) Решите систему по формулам Крамера: 3) Решите систему методом Гаусса: 5) 7) Решите систему матричным способом: 9) Решите систему: 11) 13) 15)
Вопросы к коллоквиуму
1. Определитель второго порядка: определение, элементы главной диагонали, вычисление определителя. 2. Свойства определителя. 3. Определитель третьего порядка: определение, минор для элемента аij, алгебраическое дополнение для элемента аij, разложение определителя по элементам строки (столбца), вычисление определителя. … 4. Определитель п -го порядка: нулевой определитель; единичный определитель; вычисление. 5. Матрица: определение называется, виды матриц, равные матрицы. Приведите примеры двух равных и двух неравных матриц. 6. Сумма и разность матриц: условие выполнения, правило. Приведите пример. 7. Умножение матрицы на число: правило. Приведите пример. 8. Произведение матриц: условие выполнения, правило, свойства операции умножения матриц. 9. Матрица обратная матрице А: определение, условие существования, алгоритм нахождения. 10. Методы решения систем линейных уравнений.
Задания для самостоятельного решения
1. Вычислите определитель 2-го порядка: 1) 6) 11) 2. Вычислите определитель 3-го порядка: 1) 3. Вычислите определитель, разложив его по элементам: А) первого столбца; 1) Б) первой строки; 4) В) третьего столбца; 7) Г) третьей строки 10) Д) второго столбца 13) 4. Вычислите определитель, пользуясь свойствами определителя: 1)
5. Найдите матрицу М, заданную формулой:
1) М= 2 АВ - 4 А, если 2) М= 2 В2-5А, если 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15)
6. Найдите матрицу, обратную данной:
1) 13)
7. Решить систему уравнений по формулам Крамера:
1) 7) 13)
8. Решить систему уравнений методом Гаусса:
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 вида
вида , где i =1, 2, 3, … m; j = 1, 2, 3, … n;
, где i =1, 2, 3, … m; j = 1, 2, 3, … n; , где i – номер строки, j – номер столбца. Элементы, индекс которых состоит из одинаковых цифр, образуют главную диагональ. Например, а 11 и а 22.
, где i – номер строки, j – номер столбца. Элементы, индекс которых состоит из одинаковых цифр, образуют главную диагональ. Например, а 11 и а 22. , которую называют матрицей-строкой. Если же m> 1, а n= 1, то говорят об одностолбцовой матрице, которую называют матрицей-столбцом или вектором.
, которую называют матрицей-строкой. Если же m> 1, а n= 1, то говорят об одностолбцовой матрице, которую называют матрицей-столбцом или вектором. – квадратная матрица второго порядка.
– квадратная матрица второго порядка.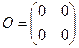 – нулевая матрица второго порядка.
– нулевая матрица второго порядка. – единичная матрица третьего порядка.
– единичная матрица третьего порядка. и
и 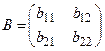 ,
,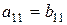 ,
,  ,
,  ,
,  , то А=В.
, то А=В. , определяется равенством
, определяется равенством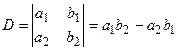 . (1)
. (1) .
. , определяется равенством
, определяется равенством . (2)
. (2)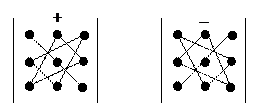
 .
.
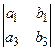 .
. =
= 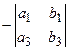 .
.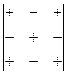 .
. .
.

 .
. .
. .
. .
.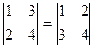 .
.
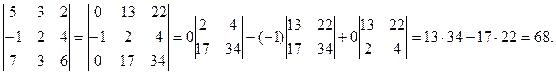
 ; 2)
; 2)  ; 3)
; 3)  .
. ; 5) второй строки
; 5) второй строки 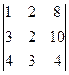 .
. ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.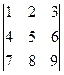 ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  ;
; ; 16)
; 16)  .
.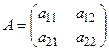 и
и  , то их суммой называется матрица
, то их суммой называется матрица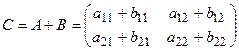 .
. ,
, – не имеет смысла.
– не имеет смысла. .
. ,
, – не имеет смысла.
– не имеет смысла. .
. ;
; .
.
 .
. .
.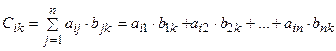 , (i =1, 2, …, n; k =1, 2, …, n),
, (i =1, 2, …, n; k =1, 2, …, n), =
=  ;
; ;
; – не имеет смысла.
– не имеет смысла. .
. ,
, .
. ,
,  ,
, 
 ,
, 
 ,
, 

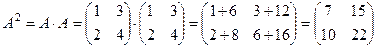 .
. , АТ =
, АТ = 
 .
.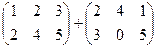 , 2)
, 2)  ,
, , 4)
, 4)  ,
, , 6)
, 6)  ,
,
 .
. ,
, 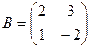 .
. .
. .
.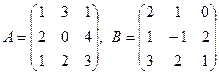 .
. .
. .
. ; б)
; б)  .
. ; 16)
; 16)  .
.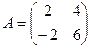 ; 18)
; 18)  ;
; , 20)
, 20)  .
. – кубическое.
– кубическое. (3)
(3) , которые при подстановки вместо неизвестных в уравнения, обращают их в верные числовые равенства (тождества). Решить систему уравнений – значит найти все ее решения.
, которые при подстановки вместо неизвестных в уравнения, обращают их в верные числовые равенства (тождества). Решить систему уравнений – значит найти все ее решения. и
и  (4)
(4)




 =
= 
 =
=  ,
,  =
=  , …,
, …,  =
= 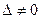 , то решение системы (3) находится по формулам Крамера:
, то решение системы (3) находится по формулам Крамера: ,
,  , …,
, …,  . (5)
. (5)
 ≠0,
≠0,  ,
,  ,
, ,
,  .
. .
.
 ,
,  ,
,  ,
, 
 , y=
, y=  , z=
, z=  .
.



 , а 3-е уравнении – на 2
, а 3-е уравнении – на 2  и вычитаем из одного другое.
и вычитаем из одного другое.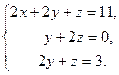
 ) и вычитаем из него 3-е.
) и вычитаем из него 3-е.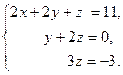
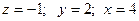 .
.
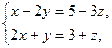

 и получим решение системы в виде
и получим решение системы в виде .
. .
.
 ~
~ 
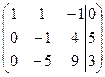 ~
~ 
 ~
~  .
.
 .
.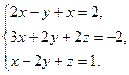
 ; Х =
; Х =  ; В =
; В =  .
. .
.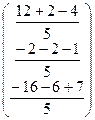 =
=  ,
, .
. 2)
2) 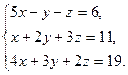
 4)
4) 
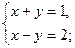 6)
6) 
 8)
8) 
 10)
10) 
 12)
12) 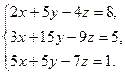
 14)
14) 

 ; 2)
; 2)  ; 3)
; 3) 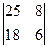 ; 4)
; 4)  ; 5)
; 5)  ;
; ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ;
; ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  , 15).
, 15).  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 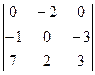 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15)  .
. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  ;
; ; 11)
; 11)  ; 12)
; 12) 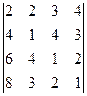 ;
; ; 14)
; 14)  15).
15). 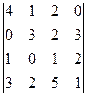 .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7) 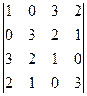 ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11) 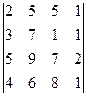 ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14) 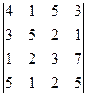 ; 15)
; 15)  .
. ,
,  ;
;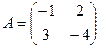 ,
,  ;
; , если
, если  ,
,  ;
; , если
, если  ,
,  ;
; , если
, если  ,
, 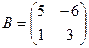 ,
,  ;
; , если
, если  ,
,  ;
;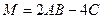 , если
, если  ,
,  ,
,  ;
; , если
, если  ,
, 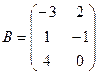 ;
;  ;
;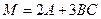 , если
, если  ,
,  ;
;  ;
; , если
, если 
 ,
,  ;
; , если
, если  ;
;  ;
;  ;
; , если
, если  ;
;  ;
; , если
, если  , если
, если  , если
, если  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10) 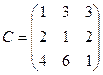 ; 11)
; 11)  ; 12)
; 12)  ;
; ; 14)
; 14)  ; 15)
; 15) 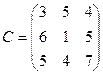 .
.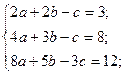 2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 
 8)
8)  9)
9)  10)
10)  11)
11)  12)
12) 
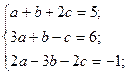 14)
14)  15)
15) 



