
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над векторами в координатной формеСодержание книги
Поиск на нашем сайте
1. Сложение векторов
Свойства: Пример.
2. Вычитание векторов
Пример.
3. Умножение вектора на число
Пример. 4. Скалярное произведение векторов Определение. Скалярным произведением двух векторов называется произведение их модулей, умноженное на косинус угла между ними
Скалярное произведение векторов можно найти по формуле
Пример. Из формул (32) и (33) можно определить угол между векторами
Пример. Свойства: 1) 2) 3) 4) Пример. Доказать, что векторы
5. Векторное произведение векторов Определение. Векторным произведением двух векторов
Свойства: 1) 2) 3) 4) Если 5) Площадь параллелограмма, построенного на векторах
Пример. Найти площадь треугольника, построенного на векторах Найдем
6. Смешанное произведение векторов Определение. Смешанным произведением трех векторов
Свойства: 1) Смешанное произведение компланарных векторов (лежащих в одной плоскости) равно нулю. 2) Четная перестановка векторов в смешанном произведении его не меняет:
3) Модуль смешанного произведения векторов
Пример. Найти объем треугольной пирамиды, построенной на векторах Найдем смешанное произведение данных векторов:
Упражнения 1. Найдите координаты и длину вектора а) А (-1; 5; 2), В (2; 5; -2); б) А (1; 3; 0), В (-2; 3; 0); в) А (4; -7; -3), В (-1; 9; 3). 2. Даны векторы 3. Коллинеарны ли векторы: а) 4. Найдите скалярное произведение векторов: а) 5. Найдите угол между векторами: а) 6. Перпендикулярны ли векторы: а) 7. Найдите векторное произведение векторов:
а) 8. Найдите площадь параллелограмма, построенного на векторах: а) 9. Найдите площадь треугольника, построенного на векторах а) 10. Найдите площадь треугольника с вершинами a) А (1; 1; 1), В (2; 3; 4) и С (4; 3; 2); б) А (0; 3; -2), В (1; -2; 2) и С (5; 0; -1). 11. Найдите смешанное произведение векторов: а) 12. Найдите объем параллелепипеда, построенного на векторах а) 13. Найдите объем треугольной пирамиды, построенной на векторах а) 14. Найдите объем треугольной пирамидыс вершинами А (0; 0; 1), В (2; 3; 5); С(6; 2; 3); D(3; 7; 2). Вопросы к коллоквиуму
1. Найти длину отрезка, координаты середины отрезка, если известны координаты точек. 2. Найти длину медианы треугольника, точки пересечения медиан треугольника, если известны координаты его вершин. 3. Написать уравнение прямой, которая проходит через две точки. 4. Написать уравнение прямой, которая проходит через данную точку параллельно данной прямой; через данную точку перпендикулярно данной прямой. 5. Найти угловой коэффициент прямой; отрезки, отсекаемые этой прямой на координатных осях. 6. Написать уравнение прямой в отрезках и общее уравнение прямой, если известны координаты точек пересечения с осями. 7. Составьте уравнение окружности, если известен ее центр и радиус. 8. Постройте окружность, укажите ее центр и радиус. 9. Определите полуоси, координаты фокусов и вершин эллипса, постройте линию. 10. Определите полуоси, координаты фокусов и вершин гиперболы, постройте линию. 11. Найдите координаты фокуса и запишите уравнение директрисы параболы, сделайте рисунок. 12. Найти координаты вектора, его длину. 13. Выполните следующие действия с векторами в координатной форме:
14. Найдите угол между прямыми АВ и ВС, используя скалярное произведение векторов. 15. Найдите площадь параллелограмма и треугольника, построенных на векторах 16. Найдите объем призмы и пирамиды, построенных на векторах
Задания для самостоятельного решения
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.107.101 (0.007 с.) |

 (29)
(29)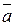 +
+  =
=  =
=  )=
)=  ,
, 
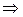
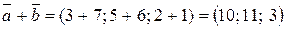 .
.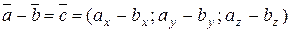 . (30)
. (30) .
. (31)
(31) .
. . (32)
. (32)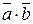 =
=  . (33)
. (33)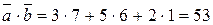 .
. . (34)
. (34) ,
, 
 ,
,  , тогда по формуле (34) находим
, тогда по формуле (34) находим  .
. )=
)=  ;
; .
. и
и  перпендикулярны. Для этого применим свойство (4) скалярного произведения векторов:
перпендикулярны. Для этого применим свойство (4) скалярного произведения векторов: 
 .
. . (35)
. (35)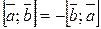 ;
; ;
;
 ;
; . (36)
. (36)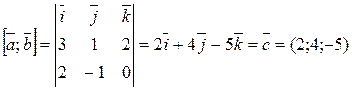 , по формуле (36)
, по формуле (36)  .
. .
. (37)
(37)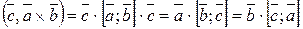 .
. . (38)
. (38) ,
,  ,
,  .
. ,
, 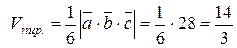 (куб.ед.).
(куб.ед.). , если
, если ,
,  и
и  . Найдите координаты вектора: а)
. Найдите координаты вектора: а) 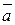 +
+ 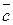 ; в) 3
; в) 3  и
и  ; б)
; б) 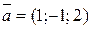 и
и  ; в)
; в)  , если А (-2; 3; 1), В (1; 5; -2), С (4; 5; -8), D (1; 3; -5)
, если А (-2; 3; 1), В (1; 5; -2), С (4; 5; -8), D (1; 3; -5) и
и  ; б)
; б)  и
и  ; в)
; в) 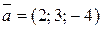 и
и  .
. и
и  ; б)
; б)  и
и 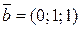 .
.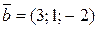 ; б)
; б)  ?
?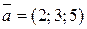 и
и  ; б)
; б)  и
и  .
.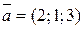 и
и  ; б)
; б)  и
и  ; в)
; в)  и
и  .
. и
и  ; б)
; б) 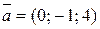 и
и 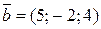 .
. ,
,  и
и  ; б)
; б) 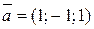 ,
, 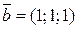 и
и  .
. ,
,  и
и  ; б)
; б)  и
и  ; в)
; в)  ,
,  и
и 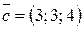 .
. ,
,  и
и  ; б)
; б)  ,
,  и
и  .
. ;
;  ;
;  ;
; 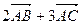 ;
;  ;
;  .
.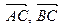 .
.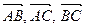 .
.


