
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное положение двух плоскостейСодержание книги
Поиск на нашем сайте
Две произвольные плоскости в пространстве по отношению друг к другу могут занимать два положения: ·плоскости пересекаются, при этом линия их пересечения всегда ·плоскости параллельны друг другу.
Условия пересечения плоскостей
Две произвольные плоскости в пространстве пересекаются по прямой линии. Как известно, две точки вполне определяют единственную прямую в пространстве. Следовательно, задача по построению линии пересечения плоскостей сводится к определению положения двух принадлежащих им обеим точек. Прямая пересечения плоскостей может быть построена и при условии, если определена одна общая для плоскостей точка и известно направление этой линии.
Условия параллельности плоскостей
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости: ·если плоскости заданы пересекающимися прямыми, то они будут параллельны в случае, когда одноименные проекции прямых, лежащих в разных плоскостях, будут параллельны; ·если плоскости заданы линиями уровня (фронталями и горизонталями), то они будут параллельны в случае, когда одноименные проекции линий уровня параллельны между собой; ·если плоскости заданы следами, то они параллельны тогда, когда параллельны их одноименные следы; ·если плоскости заданы любым другим способом, то в них необходимо построить пересекающиеся прямые (общего положения, уровня или следы) и сравнить одноименные их проекции. У параллельных плоскостей одноименные проекции пересекающихся прямых взаимно параллельны.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ
Определение взаимного положения Прямой линии и плоскости
Прямая линия и плоскость в пространстве относительно друг друга могут занимать следующие положения: ·прямая линия параллельна плоскости (частный случай — прямая лежит в плоскости); ·прямая линия пересекается с плоскостью (частный случай — прямая перпендикулярна к плоскости). Иногда на чертеже нельзя непосредственно установить положение прямой линии т и плоскости
В этом случае прибегают к некоторым вспомогательным построениям. В результате данных построений от вопроса о взаимном положении прямой линии и плоскости переходят к вопросу о взаимном положении двух прямых линий. В задачах этого типа используют метод вспомогательной плоскости. Заключается он в следующем:
- через данную прямую т проводят вспомогательную плоскость · строят линию пересечения плоскостей - заданной · устанавливают взаимное положение прямой т и линии пересечения плоскостей п. При этом возможны следующие случаи: · прямая т параллельна прямой п, следовательно, прямая т параллельна плоскости · прямая т пересекает прямую п, следовательно, прямая т пересекает плоскость
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.218 (0.009 с.) |

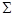 (рис. 7.1).
(рис. 7.1).
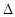 . Подбор вспомогательной плоскости производится таким образом, чтобы решение задачи было наиболее простым;
. Подбор вспомогательной плоскости производится таким образом, чтобы решение задачи было наиболее простым;


