
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод центрального проецированияСодержание книги
Поиск на нашем сайте
Начертательная геометрия
Конспект лекций для студентов специальности 190701 «Организация перевозок и управление на транспорте (ж. д. транспорт)» дневной и заочной форм обучения
Самара 2005
УДК 514.18 А72
Рецензент
Доктор технических наук, профессор кафедры «Строительные и дорожные машины и технология машиностроения» СамГАПС
В.М. Морогов
Печатается по решению редакционно-издательского совета Самарской государственной академии путей сообщения
А72 Антипов, В.А. Начертательная геометрия: Курс лекций [Текст]. – Самара: СамГАПС, 2005. – 64 с.
Настоящее издание предназначено для студентов, изучающих дисциплину «Начертательная геометрия». Конспект лекций имеет своей целью помочь студенту в освоении теоретических основ начертательной геометрии. Изложение разделов курса построено по принципу «от простого к сложному». Все разделы иллюстрированы чертежами и наглядными рисунками, что призвано облегчить восприятие студентами приведенного материала. С помощью настоящего пособия студент сможет получить необходимый минимум знаний по указанному курсу, достаточный для использования при решении практических задач.
Под редакцией доктора технических наук, профессора кафедры «Инженерная графика» Самарской государственной академии путей сообщения О.П. Мулюкина
©СамГАПС, 2005 ©Антипов В.А., 2005 ПРЕДИСЛОВИЕ
В любой отрасли промышленности для изготовления отдельных деталей и составных частей машин создаются их геометрические (идеальные) образы, которые называются чертежами. Под чертежами понимают плоское изображение идеальных геометрических очертаний и размеров технического объекта, выполненное таким образом, чтобы можно было представить его объёмные формы. В связи с этим у будущего инженера важно выработать и развить пространственное (объемное) «видение» плоского изображения. Это позволяет не только правильно читать и понимать плоские чертежи, но и, используя целый ряд правил и положений, грамотно их выполнять. Все эти вопросы рассматриваются студентами вузов при изучении первой общепрофессиональной дисциплины «Инженерная графика». Важнейшей составной частью ее является курс начертательной геометрии, который в силу его большой значимости во многих образовательных стандартах выделен в отдельную дисциплину. Изучение этого курса преследует следующие основные цели: · ознакомить студента с различными методами проецирования предмета на плоскость для получения какого-либо изображения; · развить пространственное представление об объёмных формах технических объектов и их составляющих частей по изображению этих объектов на плоскостях; · сформировать и закрепить в сознании человека систему правил для решения графическими методами технических задач проектирования; · выработать у студента предварительные навыки составления чертежей технических объектов и умение чтения чертежей. В отличие от других изданий лекционный курс минимизирован до объема, предусмотренного рабочей программой по начертательной геометрии для студентов специальности 190701 и достаточного для практических занятий, самостоятельной работы студента, выполнения графических заданий по курсу. Рекомендуется для студентов родственных специальностей, изучающих курс начертательной геометрии и обучаемых в вузах министерства транспорта Российской Федерации.
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ При изучении курса приняты следующие обозначения: 1.1 Плоскости проекций: горизонтальная — П1; фронтальная — П2; профильная — П3; дополнительная — П4, П5...аксонометрическая — П'. 1.2 Точки: А, В, С, Д... или 1,2, 3,4... 1.3 Проекции точек на плоскость: П1— А1,В1,С1,Д1... или 11,21, 3,1,41; П2 — А2,В2,С2,Д2... или 12,22, 3,2,42; П3 — А3,В3,С3,Д3... или 13,23, 3,3,43; П' — А`,В`,С`,Д`... или 1`,2`, 3`,4` 1.4 Точки на развертках: А0, В0, Со, Д0- - - или 10, 20, З0, 40... 1.5 Последовательный ряд точек: 1.6 Линии: a,b,c,d... 1.7 Проекции линий на плоскость: П1— a1,b1,c1,d1... П2 — a2,b2,c2,d2... П3 — a3,b3,c3,d3... 1.8 Линии уровня: горизонтальная (горизонталь) — h; фронтальная (фронталь) — f; профильная —р. 1.9 Координатные оси проекций: абсцисс — x; ординат — y; аппликат — z. 1.10 Новые оси абсцисс, полученные при замене плоскостей проекций: х1,x2... 1.11 Аксонометрические оси координат: x`,y`,z`. 1.12 Последовательный ряд линий: 1.13 Прямая, проходящая через точки А и В: АВ. 1.14 Плоскости (поверхности):
ОБРАЗОВАНИЕ ПРОЕКЦИЙ. МЕТОДЫ ПРОЕЦИРОВАНИЯ
Плоский чертеж какого-либо технического объекта может состоять из нескольких изображений, по которым и создается представление об объемных формах геометрического тела. Такие плоские изображения называются проекциями рассматриваемого объекта. Под проекцией любой точки понимают ее как бы «теневое» отображение на какой-либо плоскости. Так, если поместить материальную точку 1 между источниками света (световых лучей) 2 и какой-либо плоскостью 3 (рис. 2.1), то на этой плоскости увидим тень 4 этой точки, которую и принято называть проекцией точки.
Рис. 2.1 Взаимное положение источника света и плоскости может быть произвольным. В зависимости от величины угла между лучом 2-1-4 и плоскостью 3 возможны два принципиально отличных варианта проекций точки: ·значение угла не равно 90°, тогда проекция точки называется косоугольной; ·значение угла равно 90° (прямой угол), тогда проекция называется прямоугольной, или ортогональной (от греч. orthogonios - прямо угольный). Курс начертательной геометрии рассматривает два основных метода проецирования: центральный и параллельный. Рис. 2.2 Рис. 2.3
Решения инженерных задач
Наибольшее практическое применение нашёл метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций, одна из которых расположена горизонтально, а другая - вертикально. Они соответственно получили обозначения: горизонтальная плоскость проекций – П1, и фронтальная — П2. Эти плоскости пересекаются между собой под прямым углом, образуя линию пересечения — ось х, и делят пространство на четыре четверти, которые принято обозначать против хода часовой стрелки римскими цифрами I, II, III и IV (рис. 2.4). В случае недостаточной информативности об объекте по двум проекциям на указанные плоскости П1 и П2 используют третью плоскость П3, перпендикулярную одновременно П1 и П2. Она называется профильной плоскостью проекций. Плоскость Пзпересекается с плоскостью П1образуя ось у, и с плоскостью П2, образуя ось z. Указанные плоскости делят всё пространство вокруг уже на восемь частей, которые называются октантами и обозначаются римскими цифрами от I до VIII.
ПРОЕЦИРОВАНИЕ ТОЧКИ
Точки плоскостям проекций
Например, точка А принадлежит: - горизонтальной плоскости проекций П1если - фронтальной плоскости проекций П2, если - профильной плоскости проекций П3, если
Любая точка лежит на оси проекций, если её смежные две проекции совпадают в пространстве. Так, точка А лежит на оси х, если А1 совпадает с А2; на оси у, если A2 совпадает с А3, и оси z, если А2 совпадает с А3.
Задание прямой в пространстве
Любая прямая в пространстве может быть задана: · двумя точками, принадлежащими этой прямой; · одной точкой, принадлежащей данной прямой, и ее направлением. В первом случае задаются координаты двух заданных точек, во втором — координаты одной точки и направление прямой. Следы прямой
Следом прямой называется точка пересечения прямой с плоскостью проекции. Горизонтальным следом прямой называют точку пересечения прямой с горизонтальной плоскостью проекций (рис. 4.5). Горизонтальный след обозначают буквой Н. При этом координата z точки Н равна нулю. Следовательно, для нахождения горизонтального следа прямой на ней определяют точку Н с нулевой координатой z (рис. 4.5). Фронтальным следом прямой называют точку пересечения прямой с фронтальной плоскостью проекции (рис. 4.5). Обозначают фронтальный след буквой F. Координата у точки F равна нулю. Следовательно, для нахождения фронтального следа F прямой на ней определяют точку, имеющую нулевую координату у. Профильным следом прямой называют точку пересечения прямой с профильной плоскостью проекции. Обозначают профильный след буквой Р. Координата х точки Р равна нулю. Пересекая плоскости проекции, прямая переходит из одной четверти пространства в другую. Линия общего положения может пройти через три четверти пространства; линия уровня и проецирующая линия — через две четверти.
4.4 Длина отрезка прямой и углы наклона прямой
Отрезок прямой, параллельной какой-либо плоскости проекции, проецируется на данную плоскость без искажения (в натуральную величину) (рис. 4.6). Так, отрезок АВ параллелен плоскости П1(рис. 4.6, а), следовательно, длина отрезка равна его горизонтальной проекции A1 B1. Угол
Отрезок CD параллелен плоскости П2(рис. 4.6, б), следовательно, длина отрезка равна его фронтальной проекции C2D2.Угол α определяет угол наклона отрезка CD к плоскости П1. Отрезок EFпараллелен плоскости Пз(рис. 4.6, в), следовательно, длина отрезка равна его профильной проекции E3F3.Углы наклона отрезка к плоскостям П1и П2 определяют соответственно углы Если отрезок не параллелен плоскостям проекции, то для определения натуральной величины его и угла наклона к плоскости проекции необходимо выполнить дополнительные построения: построить вспомогательный прямоугольный треугольник, один катет которого равен проекции отрезка на плоскость П1или П2, а другой - разности удалений концов отрезка от той плоскости, на которой строится треугольник (рис. 4.7).
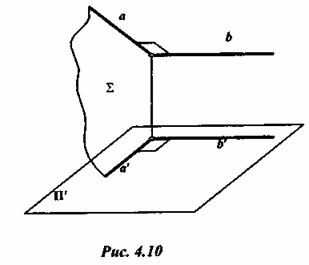
Один катет вспомогательного треугольника равен горизонтальной проекции отрезка A1 B1а другой – В1 B0 - разности координат z концов отрезка (точек А и В). Гипотенуза А1В0определяет действительную длину отрезка АВ. Угол Теорема о проецировании прямого угла. Для того чтобы прямой угол проецировался в виде прямого угла, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекции, а вторая сторона не перпендикулярна к ней (рис. 4.10).
ПЛОСКОСТЬ
Задание плоскости
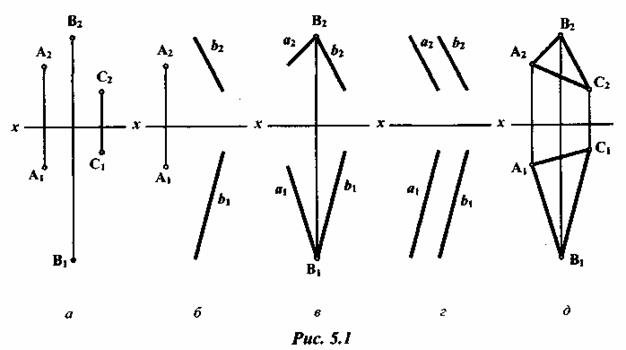
Плоскость в пространстве можно задать: ·тремя точками, не лежащими на одной прямой (рис. 5.1, а); ·прямой и не принадлежащей ей точкой (рис. 5.1, б); ·двумя пересекающимися прямыми (рис. 5.1, в); ·двумя параллельными прямыми (рис. 5.1, г); ·любой плоской фигурой (рис. 5.1, (3).
Каждый из перечисленных способов задания плоскости допускает переход к любому другому, т.к. положение прямой в плоскости определяется двумя ее точками или одной точкой и направлением этой прямой. Часто применяется способ задания плоскости с помощью прямых линий (взаимно пересекающихся или параллельных), по которым данная плоскость пересекается с плоскостями проекций П1,П2, П3.Это задание плоскости следами сохраняет наглядность изображения (рис. 5.2).
Следы плоскости
Линия пересечения рассматриваемой плоскости с плоскостью проекций (П1, П2, П3)называется следом плоскости. Иными словами, след плоскости — прямая, лежащая в плоскости проекций. Следу присваивается наименование той плоскости проекций, которой он принадлежит. Например, горизонтальный след получен при пересечении заданной плоскости с плоскостью П1 и обозначается
Плоскостей проекций
Любая, произвольно взятая в пространстве, плоскость может занимать общее или частное положение. Плоскостью общего положения называется плоскость, которая не перпендикулярна ни к одной из плоскостей проекций (см. рис. 5.2). Все остальные плоскости (кроме плоскостей проекций) относятся к плоскостям частного положения подразделяются на проецирующие плоскости и плоскости уровня. |Проецирующей называется плоскость, перпендикулярная к одной
Горизонтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизонтальным следом
Фронтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости Профильно-проецирующая плоскость Т (T1, T2) перпендикулярна к профильной плоскости проекции П3 (рис. 5.5).
Профильные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с профильным следом плоскости Т3.
Углы Профильно-проецирующая плоскость может проходить через ось x: (рис. 5.6). Следы этой плоскости
Плоскостью уровня называется плоскость, перпендикулярная одновременно к двум плоскостям проекций и параллельная третьей. Таких плоскостей три разновидности (рис. 5.7): · горизонтальная плоскость уровня перпендикулярна к П2, П3 и параллельна П1(рис. 5.7, а); · фронтальная плоскость уровня перпендикулярна к П1 , П3 и параллельна П2(рис. 5.7, б); · профильная плоскость уровня перпендикулярна к П1 , П2 и параллельна П3(рис. 5.7, в).
Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов.
К плоскостям проекций
Плоскость общего положения, расположенная в пространстве Линии наибольшего наклона плоскости - это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленное данной плоскостью и плоскостью проекций (рис. 5.10).
Прямой линии и плоскости
Прямая линия и плоскость в пространстве относительно друг друга могут занимать следующие положения: ·прямая линия параллельна плоскости (частный случай — прямая лежит в плоскости); ·прямая линия пересекается с плоскостью (частный случай — прямая перпендикулярна к плоскости). Иногда на чертеже нельзя непосредственно установить положение прямой линии т и плоскости
В этом случае прибегают к некоторым вспомогательным построениям. В результате данных построений от вопроса о взаимном положении прямой линии и плоскости переходят к вопросу о взаимном положении двух прямых линий. В задачах этого типа используют метод вспомогательной плоскости. Заключается он в следующем: - через данную прямую т проводят вспомогательную плоскость · строят линию пересечения плоскостей - заданной · устанавливают взаимное положение прямой т и линии пересечения плоскостей п. При этом возможны следующие случаи: · прямая т параллельна прямой п, следовательно, прямая т параллельна плоскости · прямая т пересекает прямую п, следовательно, прямая т пересекает плоскость
Основные положения
Обратимся к рисунку 8.1, на котором изображена плоскость Прямая n перпендикулярна к любой прямой плоскости Если Угол между прямой п и фронталью Если
Если прямая перпендикулярна к плоскости, то ее проекции перпендикулярны к одноименным проекциям линий уровня этой плоскости. .
На рисунке 8.2 через точку N проведена прямая n, перпендикулярная к плоскости В том случае, когда плоскость задана следами (рис. 8.3), проекции перпендикуляра располагаются перпендикулярно к одноименным следам плоскости: Рисунок 8.2 позволяет утверждать, что изображенные на нем прямая n и плоскость
Плоскость, перпендикулярную к данной прямой, определяют с помощью пересекающихся линий уровня. На рисунке 8.4 (а - условие, 6 - решение) через данную точку А проведена плоскость
На рисунке 8.5 показана прямая, перпендикулярная к горизонтально проецирующей плоскости. Очевидно, эта линия является горизонталью. На рисунке 8.6 изображена прямая, перпендикулярная к фронтально проецирующей плоскости. Она является фронталью. На рисунке 8.7 изображена прямая п (MN), перпендикулярная к профильно проецирующей плоскости Это не должно нас удивлять, так как Если требуется определить, перпендикулярна ли некоторая прямая т к заданной плоскости При совпадении линии m и n прямая m перпендикулярна к плоскости
Примеры решения задач
8.2.1 Задание: опустить перпендикуляр из точки А на плоскость Решение: исходя из принципа перпендикулярности прямой и плоскости (прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости), необходимо в плоскости провести две пересекающиеся прямые, а именно горизонталь h и фронталь
Затем из точки А проводим нормаль n к плоскости
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ Замена плоскостей проекций
Суть метода заключается в том, что одна из плоскостей проекций заменяется на новую плоскость проекций, при этом последнюю проводят перпендикулярно к незаменяемой плоскости. При такой замене величина координаты любой точки на вводимой плоскости будет такой же, как координаты той же точки на заменяемой плоскости. Например, если заменить фронтальную плоскость проекций П2на новую плоскость П4(рис. 9.1, а), то последняя должна быть перпендикулярна к плоскости П1 а расстояние от проекции точки А4 до оси x1 будет равно расстоянию от проекции точки А2 до оси х. Новая ось проекции х1 проводится так, как этого требует решение задачи. В рассматриваемом случае она проведена произвольно.
При замене горизонтальной плоскости П1на новую плоскость П5(рис. 9.1, б) сохраняется неизменная координата.);. При решении конкретной задачи таких замен может быть выполнено последовательно несколько. Главные условия этих действий — сохранение ортогонального проецирования в новой системе проекций и величин соответствующих координат. Пусть дана прямая общего положения АВ (рис. 9.2). Необходимо преобразовать чертеж отрезка АВ таким образом, чтобы прямая стала проецирующей, т.е спроецировалась на одну из плоскостей проекции в точку. Такое преобразование с заменой плоскостей выполняется в два этапа.
На первом этапе новую плоскость, например П4, вводят взамен фронтальной плоскости П2,параллельно прямой АВ.Новую ось проекций x1 проводят параллельно горизонтальной проекции прямой A1B1.Далее проводят от горизонтальной проекции линии связи, перпендикулярные к новой оси проекций, и на них откладывают координаты z, т.е. расстояние от оси проекций до фронтальных проекций точек. Новая проекция А4В4будет определять натуральную длину отрезка АВ.Одновременно определяется угол наклона прямой к плоскости проекций, в рассматриваемом примере к горизонтальной плоскости П1 – угол На втором этапе в системе плоскостей П1/П4плоскость проекций П1заменяют на П5.При этом ось х2 проводят перпендикулярно к проекции А4В4.В новой системе плоскостей проекций П4/П5прямая заняла проецирующее положение, т.е. она стала перпендикулярна к плоскости П5, и на нее прямая спроецировалась в точку, а концы отрезка АВсовпали на проекции А5 Метод применяется для определения расстояния между параллельными и скрещивающимися прямыми, величины двугранного угла, натуральной величины плоской фигуры и различных ее параметров. В том случае, если прямые являются прямыми уровня, т.е. параллельны одной из плоскостей проекций, первый этап решения опускается и преобразование начинается со второго этапа.
Метод совмещения плоскостей
Этот метод является частным случаем метода вращения вокруг линии уровня. В качестве оси вращения выбирается линия пересечения плоскости, в которой лежит та или иная фигура, с одной из плоскостей проекций. Иначе говоря, осью вращения служит горизонтальный или фронтальный след плоскости. При этом каждая точка, принадлежащая рассматриваемой фигуре, при вращении перемещается в плоскости, перпендикулярной к следу той плоскости, в которой она лежит. Например, плоскость Для решения поставленной задачи берут на фронтальном следе
Примеры решения задач
Ниже приведены решения одной и той же задачи вышеописанными методами.
9.6.1 Задание: определить натуральную величину треугольника общего положения ABC,заданного проекциями вершин A1 B1 C1и А2 В2 С2 (рис. 9.8), а также угол наклона плоскости треугольника к П1.
1) Решение методом замены плоскостей проекций (рис. 9.9). Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет в пространстве параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невозможно. Она решается в два этапа: при первой замене плоскостей проекций получают плоскость треугольника ABC,перпендикулярную к новой плоскости проекций, при второй замене - получают плоскость треугольника, параллельную новой плоскости проекций. Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A1B1C1 проводят ось x1новой системы плоскостей проекций П1 / П4перпендикулярно к горизонтальной проекции горизонтали h1. В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П4. На линиях проекционной связи в новой системе откладывают координаты z точек А, В, С с фронтальной проекции исходной системы плоскостей П1/П2.При соединении новых проекций А4, B 4, С4 получают прямую линию, в которую спроецировалась плоскость треугольника ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П1 - угол Второй этап. Выбираем новую плоскость проекции П5,параллельную плоскости треугольника, т.е. новую ось x2 проводят параллельно С4А4В4на произвольном расстоянии. Пол
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.016 с.) |

 ...
... ...
... ….
….

 , а А2
, а А2  оси х и A3
оси х и A3  , а А1
, а А1  , а А1
, а А1  между осью х и горизонтальной проекцией отрезка определяет угол наклона отрезка АВ к плоскости П2.
между осью х и горизонтальной проекцией отрезка определяет угол наклона отрезка АВ к плоскости П2.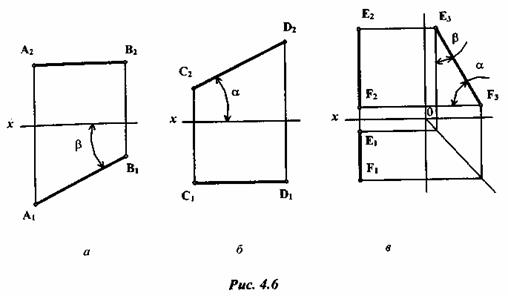
 и
и 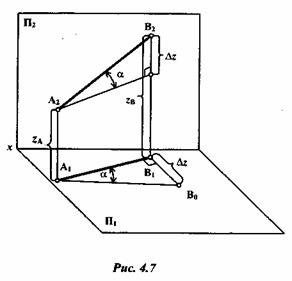

 , фронтальный — с плоскостью П2 (
, фронтальный — с плоскостью П2 (  ), профильный — с плоскостью П3(
), профильный — с плоскостью П3( ). Два следа одной и той же плоскости пересекаются на оси проекции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости
). Два следа одной и той же плоскости пересекаются на оси проекции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости 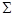 (рис. 5.2) совпадает со своей горизонтальной проекцией
(рис. 5.2) совпадает со своей горизонтальной проекцией  перпендикулярна к горизонтальной плоскости проекции П1 (рис. 5.3).
перпендикулярна к горизонтальной плоскости проекции П1 (рис. 5.3).
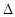 (
(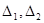 ) перпендикулярна к фронтальной плоскости П2 (рис. 5.4).
) перпендикулярна к фронтальной плоскости П2 (рис. 5.4).


 = T^П1;
= T^П1;  = Т^П2 ), проецируются на плоскость П3без искажений. Горизонтальный и фронтальный следы плоскости параллельны оси х.
= Т^П2 ), проецируются на плоскость П3без искажений. Горизонтальный и фронтальный следы плоскости параллельны оси х.

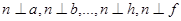 . Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плоскость проекций прямым углом, так как его сторона h||П1.
. Каждый такой прямой угол проецируется на плоскость проекций в виде некоторого угла, но угол между прямой n и горизонталью плоскости h проецируется на горизонтальную плоскость проекций прямым углом, так как его сторона h||П1. , то
, то  .
. плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона
плоскости проецируется на фронтальную плоскость проекций прямым углом (его сторона  .
.

 .
. .
.
 ). Фронталь этой плоскости может быть также проведена через точку А, но может пересекать горизонталь и в любой другой точке, поскольку все они находятся в искомой плоскости. На рисунке 8.4 фронталь f2 проходит через точку В
). Фронталь этой плоскости может быть также проведена через точку А, но может пересекать горизонталь и в любой другой точке, поскольку все они находятся в искомой плоскости. На рисунке 8.4 фронталь f2 проходит через точку В  .
.

 и
и  мы еще не определим величину искомого перпендикуляра.
мы еще не определим величину искомого перпендикуляра. , а перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой прямой к двум пересекающимся прямым плоскости. Для решения задачи нужно построить профильный след. Тогда
, а перпендикулярность прямой и плоскости обеспечивается перпендикулярностью этой прямой к двум пересекающимся прямым плоскости. Для решения задачи нужно построить профильный след. Тогда  .
.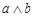 ) и найти его основание точку В.
) и найти его основание точку В.

 . Если плоскость задана следами, то
. Если плоскость задана следами, то  и
и  (рис. 8.10). Основание перпендикуляра определяется как точка пересечения его с плоскостью. Для этого нужно провести через нормаль проецирующую плоскость
(рис. 8.10). Основание перпендикуляра определяется как точка пересечения его с плоскостью. Для этого нужно провести через нормаль проецирующую плоскость  , найти линию пересечения l(l1,l2)плоскостей
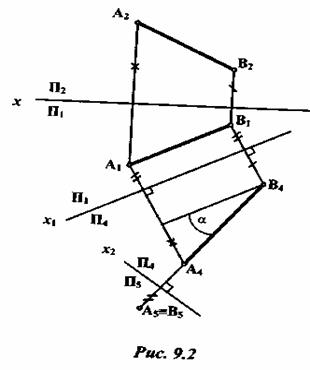
, найти линию пересечения l(l1,l2)плоскостей  ).
).
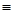 В5.
В5. , заданную своими следами
, заданную своими следами  и
и  , необходимо совместить с горизонтальной плоскостью проекций П1 (рис. 9.7).
, необходимо совместить с горизонтальной плоскостью проекций П1 (рис. 9.7). . Точка 10 принадлежит одновременно и плоскости П1 и новому (совмещенному) положению плоскости
. Точка 10 принадлежит одновременно и плоскости П1 и новому (совмещенному) положению плоскости 





