
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное положение прямых в пространствеСодержание книги
Поиск на нашем сайте
Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися. Если две прямые параллельны, то их одноименные проекции взаимно параллельны (рис. 4.8). Если две прямые пересекаются, то точки пересечения одноименных проекций принадлежат одной линии связи (рис. 4.9). В частном случае пересекающиеся прямые могут быть перпендикулярными. Дано: a Доказать, что a' Для доказательства через прямые а' и а вводится дополнительная плоскость
Прямая а' принадлежит плоскости Если две прямые не параллельны и не пересекаются, т.е. не лежат в одной плоскости, то они являются скрещивающимися (рис. 4.11). Взаимное положение двух прямых при наличии профильной прямой устанавливается по третьей проекции или каким-либо иным способом. На рис. 4.12 изображены две скрещивающиеся прямые, хотя их горизонтальные и фронтальные проекции пересекаются, а профильные — параллельны между собой.
ПЛОСКОСТЬ
Задание плоскости
Плоскость в пространстве можно задать: ·тремя точками, не лежащими на одной прямой (рис. 5.1, а); ·прямой и не принадлежащей ей точкой (рис. 5.1, б); ·двумя пересекающимися прямыми (рис. 5.1, в); ·двумя параллельными прямыми (рис. 5.1, г); ·любой плоской фигурой (рис. 5.1, (3).
Каждый из перечисленных способов задания плоскости допускает переход к любому другому, т.к. положение прямой в плоскости определяется двумя ее точками или одной точкой и направлением этой прямой. Часто применяется способ задания плоскости с помощью прямых линий (взаимно пересекающихся или параллельных), по которым данная плоскость пересекается с плоскостями проекций П1,П2, П3.Это задание плоскости следами сохраняет наглядность изображения (рис. 5.2).
Следы плоскости
Линия пересечения рассматриваемой плоскости с плоскостью проекций (П1, П2, П3)называется следом плоскости. Иными словами, след плоскости — прямая, лежащая в плоскости проекций. Следу присваивается наименование той плоскости проекций, которой он принадлежит. Например, горизонтальный след получен при пересечении заданной плоскости с плоскостью П1 и обозначается
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.112.33 (0.008 с.) |

 b; плоскость П`, b||П`(рис.4.10).
b; плоскость П`, b||П`(рис.4.10).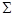 . Прямая b перпендикулярна к плоскости
. Прямая b перпендикулярна к плоскости 

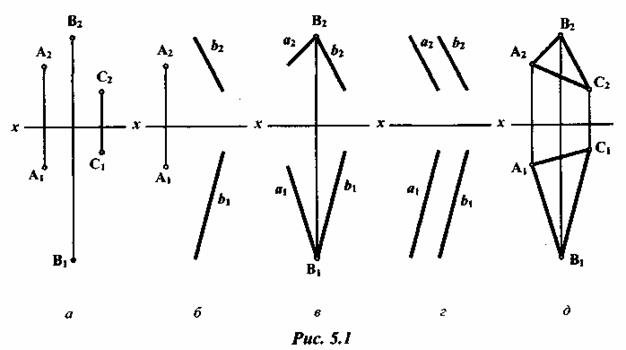

 , фронтальный — с плоскостью П2 (
, фронтальный — с плоскостью П2 (  ), профильный — с плоскостью П3(
), профильный — с плоскостью П3( ). Два следа одной и той же плоскости пересекаются на оси проекции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости
). Два следа одной и той же плоскости пересекаются на оси проекции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости 


