
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение доверительного интервала для коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Распределение выборочного коэффициента корреляции сложное, поэтому часто пользуются преобразованием Фишера для аппроксимации точного распределения коэффициента корреляции. При больших значениях n распределение выборочного коэффициента корреляции r стремится к нормальному z. Преобразование Фишера:
Для преобразованного z стандартная ошибка среднего равна Таким образом, двусторонний доверительный интервал для z будет определяться:
Нижняя граница: Верхняя граница:
Для
Для построения доверительного интервала для коэффициента корреляции сделаем обратное преобразование, получим:
Функциональная связь такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов. Корреляционная связь такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов. Практическое значение установления корреляционной связи. Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.) Зависимость параллельных изменений нескольких признаков от какой- то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др. Вычисление ошибки коэффициента корреляции o ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):
o ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):
Оценка достоверности коэффициента корреляции, полученного Методом ранговой корреляции и методом квадратов Способ 1 Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%. Способ 2 Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%. Коэффициент частной корреляции. Коэффициент частной корреляции показывает степень (тесноту) взаимосвязи двух переменных относительно друг друга, без учета влияния третьей переменной. Для вычисления частного коэффициента корреляции между тремя переменными требуется знать их коэффициенты корреляции Пирсона. Формула частного коэффициента корреляции для коэффициента корреляции Пирсона следующая:
где
Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели. Для качественной оценки тесноты связи можно использовать следующую классификацию: 0.1- 0.3- слабая связь 0.3-0.5 – умеренная связь 0.5-0.7- заметная связь 0.7-0.9- тесная связь 0.9-0.99- весьма тесная Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции. Для случая зависимости Y от двух факторов можно вычислить 2 коэффициента частной корреляции.
билет №_14_ Машинные коды, язык ассемблера, языки программирования высокого уровня. Библиотеки стандартных программ. Интерпретаторы, компиляторы и трансляторы.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.007 с.) |





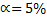 и
и 
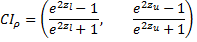



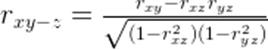
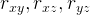 коэффициенты корреляции r-Пирсона исследуемых переменных между собой.
коэффициенты корреляции r-Пирсона исследуемых переменных между собой.


