Множественная корреляция и регрессия

При анализе взаимосвязей социально-экономических явлений как правило выясняется, что на результат влияет целый ряд факторных признаков, основные из которых следует включить в регрессионную модель. При этом следует помнить, что все факторы учесть в модели невозможно по целому ряду причин: часть факторов просто неизвестна современной науке, по части известных факторов нет достоверной информации или количество включаемых в модель факторов может быть ограничено объемом выборки (количество факторных признаков должно быть на порядок меньше численности изучаемой совокупности).

Множественная регрессия описывает форму связи в виде уравнения множественной регрессии или регрессионной модели (табл.4).

Таблица 4. Основные виды множественной регрессии

Наименование формы регрессии	Вид уравнения регрессии
Линейная	= а0 + a1x1+ … +amxm
Гиперболическая	= а0 + a1 (1/x1) + … +am(1/xm)
Параболическая	= а0 + a1x1^2+ … +am xm^2
Степенная	= а0 x1 ^a^1 x2 ^a^2… xm ^a^m

Где – теоретическое значение результативного признака (y) при определенных значениях факторных признаков (x_1, x _2,…, x _m), подставленных в регрессионное уравнение;

а₀ – свободный член уравнения;

a_1,a_2,…,a_m – коэффициенты множественной регрессии.

Параметры уравнения множественной регрессии a_1,a_2,…,a_m называют коэффициентами множественной регрессии и определяют с помощью МНК путем решения системы нормальных уравнений МНК. При этом число нормальных уравнений в общем случае будет равно числу параметров. Если связь отдельного фактора с результатом не является линейной, то производят линеаризацию уравнения. Для упрощения решения системы нормальных уравнений значения всех признаков заменяют на отклонения индивидуальных значений признаков от их средних величин. Полученные коэффициенты множественной регрессии являются именованными числами и показывают, на сколько изменится результативный признак (по отношению к своей средней величине) при отклонении факторного признака от своей средней на единицу и при постоянстве (фиксированном уровне) других факторов.

Значимость коэффициентов множественной регрессии оценивается на основе t-критерия Стьюдента. t_р рассчитывают как отношение взятого по модулю коэффициента регрессии к его средней ошибке с заданными уровнем значимости (a) и числом степеней свободы d.f. = n-m-1.

Коэффициенты регрессии можно преобразовать в сравнимые относительные показатели - стандартизованные коэффициенты регрессии или b-коэффициенты (2.5.). b-коэффициент позволяет оценить меру влияния вариации факторного признака на вариацию результата при фиксированном уровне других факторов.

, (2.5.)

где

sx_i – среднее квадратическое отклонение факторного признака,

sy – среднее квадратическое отклонение результативного признака,

a_i – коэффициент регрессии при соответствующем факторном признаке x_i.

При интерпретации результатов корреляционно-регрессионного анализа часто используют частные коэффициенты эластичности (Ex_i). Коэффициент эластичности (2.6.) показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1 % и при постоянстве (фиксированном уровне) других факторов.

, (2.6.)

где

– среднее значение факторного признака,

– среднее значение результативного признака

Множественная корреляция характеризует тесноту и направленность связи между результативным и несколькими факторными признаками. Основой измерения связей является матрица парных коэффициентов корреляции (см. п.3.2). По ней можно в первом приближении судить о тесноте связи факторных признаков между собой и с результативным признаком, а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения.

Более точную характеристику тесноты зависимости дают частные коэффициенты корреляции. Их удобно анализировать, если они представлены в табличном виде. Частный коэффициент корреляции служит показателем линейной связи между двумя признаками, исключая влияние всех остальных представленных в модели факторов. Например, для двухфакторной модели частный коэффициент корреляции между y и x₁ при фиксированном x₂ (r_yx1/x2) определяется в соответствии с (2.7.).

, (2.7.)

где

r_yx1, r_yx2, r_x1x2 – парные коэффициенты корреляции.

Проверка значимости частных коэффициентов корреляции аналогична, как и для парных коэффициентов корреляции.

Множественный коэффициент корреляции (R) рассчитывается при наличии линейной связи между всеми признаками регрессионной модели. R изменяется в пределах от 0 до 1. Значимость множественного коэффициента корреляции проверяется на основе F-критерия Фишера. Например, в двухфакторной модели при оценке связи между результативным и факторными признаками для определения множественного коэффициента корреляции можно использовать формулу (2.8.).

, (2.8.)

где

d²_{y x1x2} – дисперсия результативного признака, рассчитанная по регрессионному уравнению,

s²_y – общая дисперсия результативного признака,

r_yx1, r_yx2, r_x1x2 – парные коэффициенты корреляции.

Квадрат множественного коэффициента корреляции называют множественным коэффициентом детерминации (R²). R² оценивает долю вариации результативного фактора за счет представленных в модели факторов в общей вариации результата.Множественный коэффициент детерминации обычно корректируют на потерю степеней свободы вариации по формуле (2.9.).

, (2.9.)

где

R² _корр – корректированный множественный коэффициент детерминации,

R² –множественный коэффициент детерминации,

n – объем совокупности,

m – количество факторных признаков.

Статистическая надежность регрессионного уравнения в целом оценивается на основе F-критерия Фишера: проверяется нулевая гипотеза о несоответствии представленных регрессионным уравнением связей реально существующим (H₀: a₀= a₁=a₂=…=a_m=0, R=0). Для проверки H₀ следует расcчитать значение F- критерия (F_р) и сравнить его с табличным значением (F_т), определяемым с использованием таблицы приложения 1 по заданным уровню значимости (a = 0,05) и числу степеней свободы (d.f.1 = m-1 и d.f.2 = n-m). F_р определяется из соотношения факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле (2.10.).

, (2.10.)

где

D_факт, D_ост – суммы квадратов отклонений, характеризующие факторную и остаточную вариации результативного признака. В случае однофакторного дисперсионного комплекса D_факт, и D_ост выражаются всоответствии с(2.11),

d.f.1 = m-1 – число степеней свободы факторной дисперсии,

d.f.2 = n-m – число степеней свободы остаточной дисперсии.

, (2.11.)

где

y_ij, – значения результативного признака у i–й единицы в j–й группе,

i – номер единицы совокупности,

j – номер группы,

n_j – численность j–й группы,

– средняя величина результативного признака в j–й группе,

– общая средняя результативного признака.

Если F_р > F_т, то гипотеза H₀ отвергается. При этом с вероятностью 1-a = 0,95 или 95 %принимается альтернативная гипотеза о неслучайной природе оцениваемых характеристик, т.е. признается статистическая значимостьрегрессионного уравнения и его параметров.

3. Решение задач корреляционно-регрессионного анализа статистических связей признаков на персональном компьютере в среде пакета STATISTICA

3.1. ОбЩие сведения оБ интегрированном статистическом пакете общего назначения STATISTICA

 

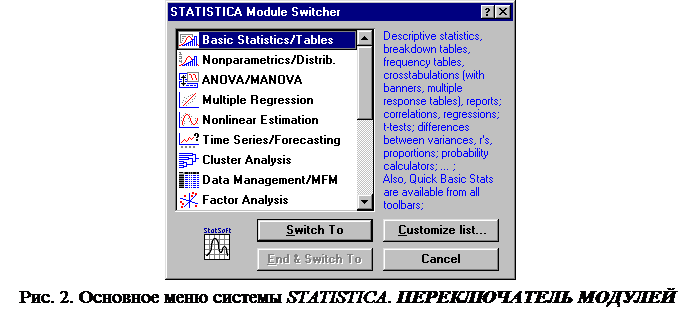
В настоящем разделе дано краткое описание системы STATISTICA, более подробные сведения о пакете приведены в /3, 4/, а также в поставляемой вместе с системой документацией фирмы-разработчика StatSoft и кратком руководстве. Следует отметить, что в процессе работы в среде STATISTICA студент может воспользоваться экранным справочником, содержащим практически всю информацию печатной документации. STATISTICA полностью удовлетворяет основным стандартам среды Windows:

Ø стандартам пользовательского интерфейса;

Ø технологии DDE — динамического обмена данными из других приложений. Благодаря поддержке DDE, нетрудно выполнить командные сценарии изнутри других приложений. Например, можно в Excel написать минипрограмму (макрос), который запускает пакет STATISTICA. После добавления в макрос специальных SQL-команд можно импортировать в пакет данные;

Ø технологии OLE — с вязывания и внедрения объектов, поддержка основных операций с буфером обмена и др. Использование OLE технологии обмена между Windows-приложениями позволяет легко интегрировать результаты, например, между WinWord и STATISTICA.

Статистический анализ данных в системе STATISTICA можно представить в виде следующих основных этапов:

Ø ввод данных в электронную таблицу с исходными данными и их предварительное преобразование перед анализом (структурирование, построение необходимых выборок, ранжирование и т. д.);

Ø визуализация данных при помощи того или иного типа графиков;

Ø применение конкретной процедуры статистической обработки;

Ø вывод результатов анализа в виде графиков и электронных таблиц с численной и текстовой информацией;

Ø подготовка и печать отчета;

Ø автоматизация процессов обработки при помощи макрокоманд, языка SCL или STATISTICA BASIC.

Интегрированный статистический пакет общего назначения STATISTICA состоит из следующих основных компонент:

Ø многофункциональной системы для работы с данными, которая включает в себя электронные таблицы для ввода и задания исходных данных, а также специальные таблицы (Scroolsheet ™) для вывода численных результатов анализа. Для сложной обработки данных в STATISTICA имеется модуль Управления данными;

Ø графической системы для визуализации данных и результатов статистического анализа;

Ø набора статистических модулей, в которых собраны группы логически связанных между собой статистических процедур (рис.2):

¾ основные статистики и таблицы;

¾ непараметрическая статистика;

¾ дисперсионный анализ;

¾ множественная регрессия;

¾ нелинейное оценивание;

¾ анализ временных рядов и прогнозирование;

¾ кластерный анализ;

¾ управление данными;

¾ факторный анализ и др.

 

 

После запуска системы STATISTICA на экране появляется Переключатель модулей (рис. 2). Модули взаимодействуют друг с другом, имея одинаковый формат системных файлов. Если пользователю нужен, например, раздел линейной регрессии, то следует выбрать модуль Multiple Regression - Множественной регрессии и выполнить команду Switch To. В любом конкретном модуле можно выполнить определенный способ статистической обработки, не обращаясь к процедурам из других модулей. Все основные операции при работе с данными и графические возможности доступны в любом статистическом модуле и на любом шаге анализа;

Ø специального инструментария для подготовки отчетов. При помощи текстового редактора, встроенного в систему, можно готовить полноценные отчеты. В пакете STATISTICA также имеется возможность автоматического создания отчетов;

Ø встроенных языков SCL и STATISTICA BASIC, которые позволяют автоматизировать рутинные процессы обработки данных в системе.