Особенности управления пакетом

К основным преимуществам управления пакетом STATISTICA можно отнести следующие:

Ø Данные можно без затруднений вводить в среду пакета, легко редактировать, создавать новые переменные, выбтрать отдельные наблюдения или «вырезать» подмножество данных по строкам и (или) по столбцам таблицы «объект-признак». Благодаря обширной панели инструментов, для выполнения большинства задач достаточно несколько щелчков мышью, так как практически для всех функций пакета имеются пиктограммы.

 

Ø В том случае, если студент забыл задать ту или иную переменную или параметр статистического метода, пакет сделает запрос к пользователю с необходимой подсказкой.

Ø Особенностью пакета является настройка функций под экран, открытый в данный момент времени. Так, при загрузке пакета в активном окне возникает список модулей, доступных пользователю в данный момент времени и пользователь может самостоятельно решить, какой вид анализа необходимо выполнить. Список модулей и порядок их следования в окне могут быть определены самим студентом, что дает ему дополнительные удобства в гибкости настройки.

Ø STATISTICA имеет возможность работы в пакетном режиме, используя свой командный язык SCL. Можно использовать и наборы команд, объединяемые в последовательности или макросы.

Ø Наиболее сильной стороной STATISTICA являются ее графические возможности. В пакете представлены множество графиков типа 2-D или 3-D, матрицы и пиктограммы. Средства управления графиками включают в себя работу одновременно с несколькими графиками, изменение размеров сложных объектов, расширенные возможности рисования и т.д.

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ

 

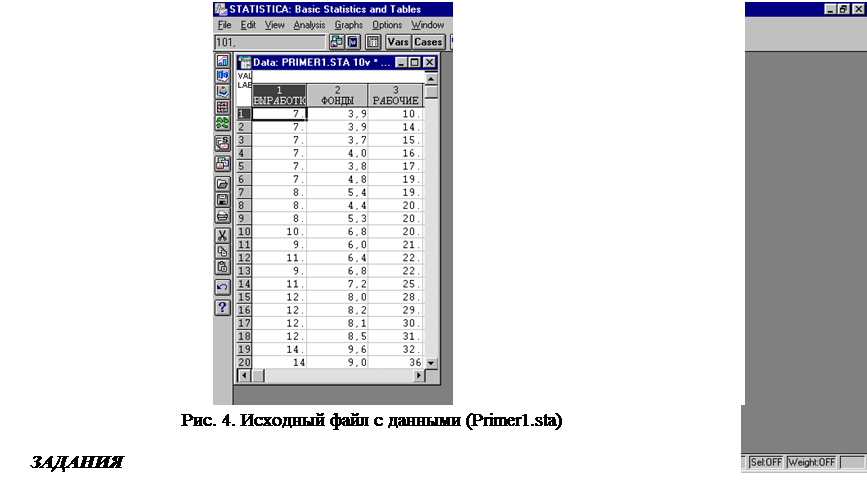
Условие задачи.

По 20 предприятиям отрасли изучается зависимость выработки продукции на 1 работника (y), тыс.руб. - " ВЫРАБОТКА " от ввода в действие новых основных фондов в % от стоимости фондов на конец года (x₁) - " ФОНДЫ " и от удельного веса рабочих высокой квалификации в общей численности рабочих (x₂), % - "РАБОЧИЕ". Данные записаны в файле пакета STATISTICA и представлены на рис.4.

 

 

1. Получить дискриптивные статистики по каждому признаку. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения метода наименьших квадратов для их изучения.

2. Составить уравнение множественной регрессии, оценить его параметры, пояснить их экономический смысл.

3. Рассчитать частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

4. Проанализировать линейные коэффициенты парной и частной корреляции.

5. Оценить значения скорректированного и нескорректированного линейных коэффициентов множественной корреляции.

6. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии в целом.

РЕШЕНИЕ ЗАДАЧИ

1. Для получения дискриптивных статистик необходимо в Переключателе модулей (см. рис.2), появившемся после запуска пакета STATISTICA, выбрать команду Basic Statistics/Tables, при этом на экране появится стартовая панель модуля Основные статистики и таблицы, в которой следует выбрать команду Descriptive statistics. Статистическую обработку данных следует предварить открытием уже существующего файла с данными через команду Open Data (рис.5), или ввести данные в компьютер через команду File/ New Data (рис.4).

 

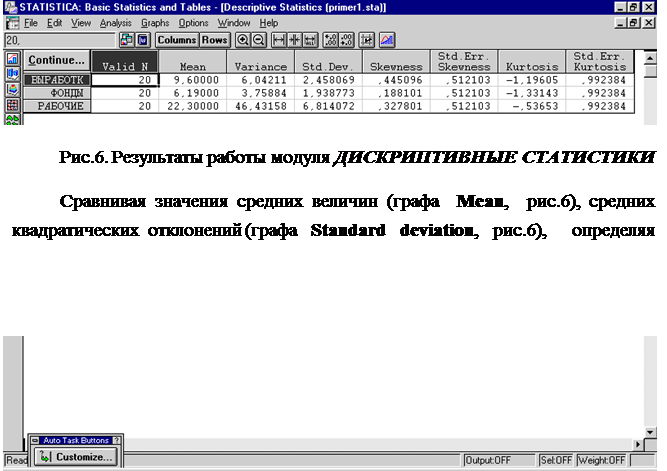
Выбрав команду OK, на экране появятся дискриптивные статистики (рис.6), анализ которых следует начать с определения показателей вариации.

коэффициент вариации (Vy = 25,6 %, Vx₁ =31,3 %, Vx₁ =30,6 %), приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%. Значения коэффициентов асимметрии (графа Skewness, рис.6), эксцесса (графа Kurtosis, рис.6) не превышают двухкратных среднеквадратических ошибок (графы Standard error of skewness, Standard error of kurtosis, рис.6). Это указывает на отсутствие значимой скошенности и остро-(плоско)вершинности фактического распределения предприятий по значениям каждого признака по сравнению с их нормальным распределением. Совокупность предприятий однородна и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

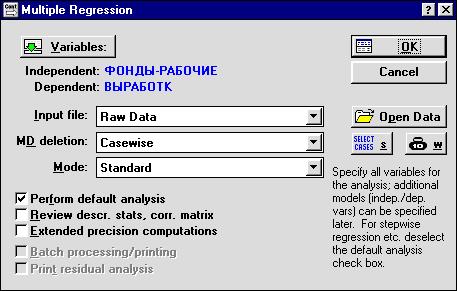
2. Для построения уравнения множественной регрессии необходимо в Переключателе модулей (рис.1) выбрать команду Multiple Regression. При этом на экране появится стартовая панель модуля Множественная регрессия (рис.7).

	Рис.7. Стартовая панель модуля Множественная регрессия

 

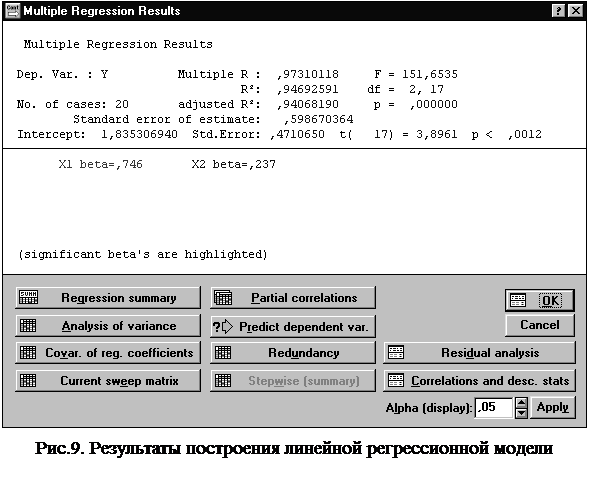
После выбора команды Variable (рис.7),, следует указать зависимую (ВЫРАБОТКА) и независимые переменные (ФОНДЫ, РАБОЧИЕ). Выбрав команду OK, получаем результаты работы модуля Множественная регрессия (рис.8-9), на основании которых студент строит уравнение линейной множественной регрессии. Свободный член и коэффициенты регрессии представлены в графе B (рис.8): а₀ = 1,835; a₁ = 0,946; a₂ = 0,086. При этом уравнение множественной регрессии примет вид: у =1,835 +0,946 x₁+ 0,086x₂

 

 

 

 

Таким образом, статистически значимыми являются коэффициенты а₀ и а₁, а коэффициент а₂ сформирован под влиянием случайных причин. Поэтому фактор x₂ можно исключить из модели как неинформативный. Аналогичный вывод можно сделать, сравнивая значения уровня значимости (графа p-level, рис. 8) c принятым нами уровнем a =0,01. Для а₀ и а₁ показатель вероятности случайных значений параметров регрессии меньше 1% (0,01 • 100%). Поэтому справедлив вывод о том, что полученные коэффициенты статистически значимы и надежны. Для а₂ делается вывод о случайной природе его значения, поскольку a =0,175 • 100%=17,5%>1%. Это позволяет рассматривать x₂ как неинформативный фактор. Его можно удалить из уравнения для улучшения модели.

Свободный член а₀ оценивает агрегированное влияние прочих (кроме учтенных в модели x₁ и x₂) факторов на результат у. Коэффициенты а₁ и а₂ указывают на то, что с увеличением x₁ и x₂ на единицу их значений у увеличивается, соответственно, на 0,9459 тыс.руб. и на 0,0856 тыс.руб. Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоставимы между собой. Для сравнения можно воспользоваться сравнимыми относительными показателями - b-коэффициентами (графа BETA, рис. 8).

3. Для определения частных коэффициентов эластичности в соответствии с (2.6.) воспользуемся коэффициентами регрессионного уравнения а₁ и а₂ и значениями средних величин результативного и факторных признаков (графа Mean, рис.6). Ex₁ = 0,61 %, Ex₂= 0,19 %. Полученные коэффициенты показывают, что с увеличением коэффициента обновления основных фондов (x₁) на 1 % от его среднего уровня выработка продукции на 1 работника (y) увеличится на 0,61 %, от своего среднего уровня. Аналогично, с увеличением доли рабочих высокой квалификации в общей численности рабочих (x₂) на 1 % от ее среднего уровня выработка продукции на 1 работника (y) увеличится на 0,19 %, от своего среднего уровня. По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат фактора x₁ по сравнению с фактором x₂.

4. Оценить тесноту парных зависимостей включенных в модель факторов можно через матрицу парных коэффициентов корреляции, а тесноту связи значений двух переменных, исключая влияниевсех других переменных, представленных в уравнении множественной регрессии можно через матрицу линейных коэффициентов частной корреляции. Для построения этих матриц в модуле Множественная регрессия (рис.9) следует последовательно выбрать

 

 

 

 

команды Correlations and desc.stats (для построения матрицы парных коэффициентов корреляции) Partial correlations (для построения матрицы линейных коэффициентов частной корреляции).

 

Полученные значения парных коэффициентов корреляции говорят о тесной связи выработки продукции на 1 работника (y) как с коэффициентом обновления основных фондов (x₁) - r _yx1 = 0,97, так и с долей рабочих высокой квалификации в общей численности рабочих (x₂) - r _yx2 = 0,94. При этом следует учитывать тесную межфакторную связь x₁ с x₂ (r _x1x2 = 0,94) примерно равную связи y с x₂. Поэтому для улучшения модели фактор x₂ можно исключить как недостаточно статистически надежный.

Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как "очищают" парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно показатель выработки продукции на 1 работника (y) связана с коэффициентом обновления основных фондов (x₁) - r _{yx1/ x2} = 0,73 по сравнению со связью y с долей рабочих высокой квалификации в общей численности рабочих (x₂) - r _{yx2/ x1} = 0,32. Этот факт также говорит в пользу исключения фактора x₂ из модели.

5. Коэффициенты линейной множественной корреляции (детерминации) представлены на рис.8-9. Коэффициент множественной корреляции R _yx1x2 = 0,973 свидетельствует о тесной связи факторных признаков с результативным.

Нескорректированный коэффициент множественной детерминации R² _yx1x2 = 0,947 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Он указывает на высокую степень обусловленности вариации результата вариацией факторных признаков. Скорректированный коэффициент множественной детерминации R² _yx1x2 = 0,941 оценивает тесноту связи с учетом степеней свободы (см. п.2.2), что позволяет его использовать для оценки тесноты связи в моделях с разным числом факторов.

Значения коэффициентов множественной детерминации позволяют сделать вывод о высокой (более 90%) детерминированности результативного признака y в модели факторными признаками x₁ и x₂.

6. Оценим статистическую надежность полученного уравнения множественной регрессии с помощью общего F-критерия, который проверяет нулевую гипотезу о статистической незначимости параметров построенного регрессионного уравнения и показателя тесноты связи (H₀: a₀= a₁=a₂=0, R _yx1x2=0).

Фактическое значение F-критерия Фишера - F_р =151,7 (см. рис.8-9). Сравним его с табличным значением F-критерия, определяемым с использованием таблицы приложения 1 по заданным уровню значимости (a = 0,05) и числу степеней свободы (в пакете STATISTICA d.f.1 = m =2 и d.f.2 = n-m-1= 17). F_т = 3,59. Поскольку F_р > F_т, то гипотеза H₀ отвергается. Так как вероятность случайного значения F_р значительно меньше 5 % (p<0,000001, см. рис.8-9)., то с вероятностью более чем95 %принимается альтернативная гипотеза. Таким образом признается статистическая значимостьрегрессионного уравнения, его параметров и показателя тесноты связи R _yx1x2.

3.3.Порядок выполнения индивидуального задания

1. Ввод исходных данных. Получив индивидуальное задание, студент создает файл с именем *.sta и заносит в него данные. Файл следует сохранить в указанном преподавателем каталоге.

2. Дикриптывно-статистический анализ данных. На данном этапе выполнения работы определяются значения средних величин, средних квадратических отклонений, значения коэффициентов асимметрии, эксцесса и их среднеквадратических ошибок по результативному и факторным признакам. Студенту следует оценить показатели вариации каждого признака и сделать вывод о возможностях применения метода наименьших квадратов для их изучения, а если необходимо, то исключить резко отклоняющиеся единицы совокупности.

3. Построение уравнения множественной регрессии. На этом этапе определяются коэффициенты множественной регрессии, составляется регрессионное уравнение, оцениваются его параметры.

4. Определение частных коэффициентов эластичности. Студент самостоятельно рассчитывает частные коэффициенты эластичности и дает на их основе сравнительную оценку силы влияния факторов на результат.

5. Анализ линейных коэффициентов парной и частной корреляции. Данный этап предусматривает построение матриц коэффициентов парной и частной корреляции и оценку целесообразности включения факторных признаков в модель.

6. Оценка коэффициентов множественной корреляции (детерминации).

7. Оценка статистической надежности полученного уравнения регрессии.

8. Оформление отчета. Титульный лист отчета должен содержать название работы, цель работы, фамилию, инициалы, курс и группу студента, выполнившего индивидуальное задание. В отчете следует отразить основные этапы выполненного задания, полученные результаты и сделать выводы по каждому этапу. Для этой цели можно использовать распечатки отчета, полученного средствами пакета STATISTICA (файл с расширением *.rtf), включая его широкие графические возможности.

9. Защита индивидуального задания. Защита индивидуального задания преследует цель оценить знания студента по вопросам построения регрессионных моделей с помощью СПП STATISTICA и интерпретации результатов корреляционно-регрессионного анализа данных. При подготовке к защите индивидуального задания студенту следует ответить на представленные в п.4 вопросы.

Вопросы для самопроверки

1. Дайте определение функциональному, статистическому и корреляционному типам связи.

2. Назовите основные условия применения корреляционно-регрессионного метода анализа статистических связей.

3. Для решения каких типов задач используется корреляционно-регрессионный метод?

4. Приведите примеры различных видов уравнений парной и множественной регрессии.

5. Дайте определение парному и множественному линейным коэффициентам корреляции.

6. Как оценивается значимость коэффициента корреляции?

7. Чем характеризуются функционально связанные между собой факторы?

8. Что характеризуют параметры регрессионного уравнения? Объясните сущность коэффициента парной линейной регрессии.

9. В чем заключается метод наименьших квадратов? Каковы основные условия его применения?

10. Как оценивается значимость параметров регрессионного уравнения?

11. Дайте определение частному коэффициенту эластичности. Что он характеризует?

12. Дайте определение стандартизованному коэффициенту регрессии. Что он характеризует?

13. Что позволяет оценить множественный коэффициент детерминации?

14. Для чего используется корректированный множественный коэффициент детерминации?

15. Как оценить статистическую надежность регрессионного уравнения в целом?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

1. Айвазян С.А. Программное обеспечение персональных ЭВМ по статистическому анализу данных. //Компьютер и экономика: экономические проблемы компьютеризации общества. М.: Наука, 1991, с.91–107.

2. Айвазян С.А., Степанов В.С. Инструменты статистического анализа данных. //«Мир ПК», 1997, №8, с.33–41.

3. Боровиков В.П., Боровиков И.П. STATISTICA. Статистический анализ и обработка данных в среде Windows. М.: Филин, 1997.

4. Боровиков В.П. Популярное введение в программу STATISTICA.- М., 1998.

5. Векслер Л.С. Статистический анализ на персональном компьютере. //«Мир ПК», 1992, №2, с.89–97.

6. Елисеева И.И., Юзбашев М.М. Общая теория статистики.- М.: Финансы и статистика, 1998.

7. Ефимова М.Р., Петров Е.В., Румянцев В.Н. и др. Общая теория статистики /Под ред. проф. Ефимовой М.Р., -М.: Инфра-М,1998.

8. Костеева Т.В., Курышева С.В., Михайлов Б.А. Эконометрика: Решение типовых задач. –СПб.: СПбГУЭФ, 1997.

9. Крастинь О.П. Разработка и интерпретация моделей корреляционных связей в экономике. – Рига: Зинате, 1983.

10. Теория статистики: Учебник /Под ред. проф. Шмойловой Р.А. -М.: Финансы и статистика,1998.

11. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. М.: Инфра-М, 1998.

Приложение 1

Таблица. Значения F-критерия Фишера при уровне значимости a =0,05

d.f. 1										¥
d.f. 2
	161,45	199,50	215,72	224,57	230,17	233,97	238,89	243,91	249,04	254,32
	18,5	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,45	19,50
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,90	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,20	3,09	2,95	2,79	2,61	2,40
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,50	2,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,77	2,60	2,42	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,29	2,07
	4,49	3.63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,45	3,59	3,20	2,96	2,81	2,70	2,55	2,38	2,19	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,38	3,52	3,13	2,90	2,74	2,63	2,48	2,31	2,11	1,88
	4,35	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,08	1,84
	4,32	3,47	3,07	2,84	2,68	2,57	2,42	2,25	2,05	1,81
	4,30	3,44	3,05	2,82	2,66	2,55	2,40	2,23	2,03	1,78

 

Продолжение табл.

d.f. 1										¥
d.f. 2
	4,28	3,42	3,03	2,80	2,64	2,53	2,38	2,20	2,00	1,76
	4,26	3,40	3,01	2,78	2,62	2,51	2,36	2,18	1,98	1,73
	4,24	3,38	2,99	2,76	2,60	2,49	2,34	2,16	1,96	1,71
	4,22	3,37	2,98	2,74	2,59	2,47	2,32	2,15	1,95	1,69
	4,21	3,35	2,96	2,73	2,57	2,46	2,30	2,13	1,93	1,67
	4,20	3,34	2,95	2,71	2,56	2,44	2,29	2,12	1,91	1,65
	4,18	3,33	2,93	2,70	2,54	2,43	2,28	2,10	1,90	1,64
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,12	3,26	2,87	2,64	2,48	2,37	2.22	2,04	1,83	1,57
	4,08	3,23	2,84	2,61	2,45	2,34	2,18	2,00	1,79	1,52
	4,06	3,21	2,81	2,58	2,42	2,31	2,15	1,97	1,76	1,48
	4,03	3,18	2,79	2,56	2,40	2,29	2,13	1,95	1.74	1,44
	4,00	3,15	2,76	2,52	2,37	2,25	2,10	1,92	1,70	1,39
	3,98	3,13	2,74	2,50	2,35	2,23	2,07	1,89	1,67	1,35
	3,96	3,11	2,72	2,49	2,33	2,21	2,06	1,88	1,65	1,31
	3,95	3,10	2,71	2,47	2,32	2,20	2,04	1,86	1,64	1,28
	3,94	3,09	2,70	2,46	2,30	2,19	2,03	1,85	1,63	1,26
	3,92	3,07	2,68	2,44	2,29	2,17	2,01	1,83	1,60	1,21
	3,90	3,06	2,66	2,43	2,27	2,16	2,00	1,82	1,59	1,18
	'3,89	3,04	2,65	2,42	2,26	2,14	1,98	1,80	1,57	1,14
	3,87	3,03	2,64	2,41	2,25	2,13	1,97	1,79.	1,55	1,10
	3,86	3,02	2,63	2,40	2,24	2,12	1,96	1,78	1,54	1,07
	3,86	3,01	2,62	2,39	2,23	2,11	1,96	1,77	1,54	1,06
	3,85	3,00	2,61	2,38	2,22	2,10	1,95	1,76	1,53	1,03
¥	3,84	2,99	2,60	2,37	2,21	2,09	1,94	1,75	1,52

Приложение 2

Таблица. Значения t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01 (двухсторонний)

Число степеней свободы d.f.	a	Число степеней свободы d.f.	a
0,10	0,05	0,01	0,10	0,05	0,01
	6,3138	12,706	63,657		1,7341	2,1009	2,8784
	2,9200	4,3027	9,9248		1,7291	2,0930	2,8609
	2,3534	3,1825	5,8409		1,7247	2,0860	2,8453
	2,1318	2,7764	4,6041		1,7207	2,0796	2,8314
	2,0150	2,5706	4,0321		1,7171	2,0739	2,8188
	1,9432	2,4469	3,7074		1,7139	2,0687	2,8073
	1,8946	2,3646	3,4995		1,7109	2,0639	2,7969
	1,8595	2,3060	3,3554		1,7081	2,0595	2,7874
	1,8331	2,2622	3,2498		1,7056	2,0555	2,7787
	1,8125	2,2281	3,1693		1,7033	2,0518	2,7707
	1,7959	2,2010	3,1058		1,7011	2,0484	2,7633
	1,7823	2,1788	3,0545		1,6991	2,0452	2,7564
	1,7709	2,1604	3,0123		1,6973	2,0423	2,7500
	1,7613	2,1448	2,9768		1,6839	2,0211	2,7045
	1,7530	2,1315	2,9467		1,6707	2,0003	2,6603
	1,7459	2,1199,	2,9208		1,6577	1,9799	2,6174
	1,7396	2,1098	2,8982	¥	1,6449	1,9600	2,5758

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по дисциплине «СТАТИСТИКА» для студентов всех форм обучения спец. 06.11.00 «Менеджмент» (Корреляционно-регрессионный анализ статистических связей

на персональном компьютере)

 

 

Составитель Наталия Юрьевна Лукьянова

 

Лицензия №

Редактор

Подписано в печать Формат 60х90 ¹/₁₆

Бум. для множит.аппаратов. Ризограф. Усл.печ.л.

Уч.-изд.л. Тираж экз. Заказ

 

 

Калининградский государственный университет,

236041, Калининград обл., ул. А.Невского,14