
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процентиль — статистическая характеристика: среднее для каждого из интервалов в выборке, ранжированной на 100 интервалов.Содержание книги
Поиск на нашем сайте
Процентили, квартили и межквартильный размах. Максимальное значение частотного распределения можно рассматривать как такое значение набора данных, с которым совпадают или являются меньше него 100% наблюдений. Когда максимальное значение рассматривают таким образом, его называют сотым процентилем. Используя такой же подход, говорят, что медиана, с которой совпадают или являются меньше ее 50% данных, является 50-ым процентилем. N-ым процентилем распределения называется значение, с которым совпадают или находятся ниже N процентов данных. Помимо медианы часто используются 25-й и 75-й процентили. 25-й процентиль называется также первым квартилем, медиана или 50-й процентиль является одновременно вторым квартилем, 75-й процентиль -третьим, а 100-й процентиль соответственно является четвертым квартилем. Межквартильный размах представляет собой центральную часть распределения и подсчитывается как разность между третьим и первым квартилями. В этом диапазоне лежит примерно половина набора нормально распределенных данных, вне его с каждой стороны находится примерно по четверти наблюдений. Чтобы подсчитать межквартильный размах, вначале нужно найти первый и третий квартили. Подобно нахождению медианы, вначале нужно упорядочить наблюдения, затем найти позицию квартиля. Значением квартиля является значение наблюдения на этой позиции, а в случае, когда квартиль попадает между двумя наблюдениями, его значение находится между значениями этих наблюдений с одной из двух сторон от этой точки. 1. Упорядочьте наблюдения по возрастанию. 2. Найдите позиции первого и третьего квартилей по формулам: позиция 1-го квартиля (Q1) = (n+1)/4 позиция 3-го квартиля (Q3) = 3*(n+1)/4 = 3-Q1 3. Определите значения 1-го и 3-го квартилей - Если квартиль приходится на наблюдение (то есть если его позиция - целое число), значение квартиля будет равно величине этого наблюдения. Например, если квартиль находится в 20-й позиции, его значение будет равно значению 20-го наблюдения. - Если квартиль попадает между двумя наблюдениями, значением квартиля будет значение меньшего наблюдения плюс указанная часть разности между двумя наблюдениями. Например, если позиция квартиля равна 20 1/4, квартиль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений. 4. Межквартильный размах равен разности значений Q3 и Q1 Рисунок 3.8 Средняя половина наблюдений частотного распределения лежит в пределах межквартильного размаха
билет №_8_ Принтеры. Виды, принципы работы, технические характеристики (в том числе что такое dpi и lpi), соотношение их с возможностями зрения человека. Свойства моментов, дисперсий и среднеквадратичных отклонений случайных величин. Свойства моментов, дисперсий и среднеквадратичных отклонений случайных величин. Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины Определения Если дана случайная величина
если математическое ожидание
если математическое ожидание в правой части этого равенства определено.[1] Абсолютные моменты могут быть определены не только для целых Замечания
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.008 с.) |


 определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то: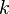 -м нача́льным моментом случайной величины
-м нача́льным моментом случайной величины  называется величина
называется величина
 в правой части этого равенства определено;
в правой части этого равенства определено;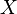 называется величина
называется величина
 и
и 


 .
.


