
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы фон неймана построения архитектуры компьютеров. Поколения эвм.Содержание книги
Поиск на нашем сайте
Принципы фон Неймана построения архитектуры компьютеров. Поколения ЭВМ. Аксиоматика Колмогорова. Вероятность и условная вероятность. Независимые события и случайные величины. Чувствительность и специфичность. Относительный риск. Вероятность и условная вероятность. Аксиоматика Колмогорова. Независимые события и случайные величины. Чувствительность и специфичность. Относительный риск. Классическое определение Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными). Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел. Классическое определение вероятности можно сформулировать следующим образом: Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно 36 (так как на каждый из 6 возможных исходов одной кости возможно по 6 вариантов исхода другой). Оценим вероятность выпадения семи очков. Получить 7 очков можно лишь при следующих сочетаниях исходов броска двух костей: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих получению 7 очков, из 36 возможных исходов броска костей. Следовательно, вероятность будет равна 6/36 или, если сократить, 1/6. Для сравнения: вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.
Геометрическое определение Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум, не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случае, обобщая классическое определение, можно прийти к геометрическому определению вероятности попадания в подобласть
В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от её площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объёма». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объёма обобщается до понятия меры некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объём» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность. Частотное (статистическое) определение Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно, существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:
где Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности — путем большого количества однородных и независимых наблюдений — тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к Аксиоматическое определение В современном математическом подходе вероятность задаётся аксиоматикой Колмогорова. Предполагается, что задано некоторое пространство элементарных событий Вероятностью (вероятностной мерой) называется мера (числовая функция)
В случае если пространство элементарных событий X конечно, то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счётного или несчётного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счётная или сигма-аддитивность, то есть выполнение свойства аддитивности для любого не более чем счётного семейства попарно несовместных событий. Это необходимо для обеспечения «непрерывности» вероятностной меры. Вероятностная мера может быть определена не для всех подмножеств множества Свойства вероятности Основные свойства вероятности проще всего определить, исходя из аксиоматического определения вероятности. 1) вероятность невозможного события (пустого множества
Это следует из того, что каждое событие можно представить как сумму этого события и невозможного события, что в силу аддитивности и конечности вероятностной меры означает, что вероятность невозможного события должна быть равна нулю. 2) если событие A включается («входит») в событие B, то есть
Это следует из неотрицательности и аддитивности вероятностной меры, так как событие 3) вероятность каждого события
Первая часть неравенства (неотрицательность) утверждается аксиоматически, а вторая следует из предыдущего свойства с учётом того, что любое событие «входит» в 4) вероятность наступления события
Это следует из аддитивности вероятности для несовместных событий и из того, что события 5) вероятность события
Это следует из предыдущего свойства, если в качестве множества 6) (теорема сложения вероятностей) вероятность наступления хотя бы одного из (то есть суммы) произвольных (не обязательно несовместных) двух событий
Это свойство можно получить, если представить объединение двух произвольных множеств как объединение двух непересекающихся — первого и разности между вторым и пересечением исходных множеств: Условная вероятность Формула Байеса Вероятность наступления события
Отсюда следует так называемая теорема умножения вероятностей:
В силу симметрии, аналогично можно показать, что также
Независимость событий События A и B называются независимыми, если вероятность наступления одного из них не зависит от того, наступило ли другое событие. С учетом понятия условной вероятности это означает, что
В рамках аксиоматического подхода данная формула принимается как определение понятия независимости двух событий. Для произвольной (конечной) совокупности событий
Выведенная (в рамках классического определения вероятности) выше формула условной вероятности при аксиоматическом определении вероятности является определением условной вероятности. Соответственно, как следствие определений независимых событий и условной вероятности, получается равенство условной и безусловной вероятностей события. Пример расчета показателя относительного риска В 1999 году в Оклахоме проводились исследования заболеваемости мужчин язвой желудка. В качестве влияющего фактора было выбрано регулярное потребление фастфуда. В первой группе находились 500 мужчин, постоянно питающихся быстрой пищей, среди которых язву желудка диагностировали у 96 человек. Во вторую группу были отобраны 500 сторонников здорового питания, среди которых язва желудка была диагностирована в 31 случае. Исходя из полученных данных была построена следующая таблица сопряженности:
1. Рассчитываем значение относительного риска:
2. Находим значения верхней и нижней границ 95% доверительного интервала по указанным выше формулам. Значение верхней границы составляет 4.55, нижней - 2.11. 3. Сравниваем полученные значения ОР и 95% ДИ с 1. Показатель относительного риска свидетельствует о наличии прямой связи между употреблением фастфуда и вероятностью развития язвы желудка. У мужчин, употребляющих картошку фри и хотдоги, язва желудка наблюдается в 3,1 раза чаще, чем среди придерживающихся здорового питания. Уровень значимости данной взаимосвязи соответствует p<0.05, так как 95% ДИ не включает в себя единицу. билет №_2_ Определение Случайная величина
Принято говорить, что событие
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из Определение Пусть
имеет биномиальное распределение с параметрами
Случайную величину Функция вероятности задаётся формулой:
где
— биномиальный коэффициент. Функция распределения Функция распределения биномиального распределения может быть записана в виде суммы:
где
Моменты Производящая функция моментов биномиального распределения имеет вид:
откуда
а дисперсия случайной величины.
Определение Выберем фиксированное число
где
Тот факт, что случайная величина Моменты Производящая функция моментов распределения Пуассона имеет вид:
откуда
Для факториальных моментов распределения справедлива общая формула:
где А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты. Виды представления информации (неформатированные тексты, гипертексты и т.д.), форматы файлов, в которых они хранятся, и программы, которые с ними работают. Векторная и растровая графика. Популярные форматы графических файлов. Проверка гипотезы Проверка гипотезы Таким образом, уровень Популярными уровнями значимости являются 10 %, 5 %, 1 %, и 0,1 %. Различные значения α-уровня имеют свои достоинства и недостатки. Меньшие α-уровни дают бо́льшую уверенность в том, что уже установленная альтернативная гипотеза значима, но при этом есть больший риск не отвергнуть ложную нулевую гипотезу (ошибка второго рода, или «ложноотрицательное решение»), и таким образом меньшая статистическая мощность. Выбор α-уровня неизбежно требует компромисса между значимостью и мощностью, и следовательно между вероятностями ошибок первого и второго рода.
Определения Пусть в (статистическом) эксперименте доступна наблюдению случайная величина
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу. В большинстве случаев статистические критерии основаны на случайной выборке Виды критической области Выделяют три вида критических областей:
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат. Определения Пусть дана выборка
где
сопоставляющий каждой реализации выборки
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.
Определение Доверительным интервалом параметра
Граничные точки доверительного интервала Толкование доверительного интервала, основанное на интуиции, будет следующим: если уровень доверия p велик (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра Более точное, хоть также не совсем строгое, толкование доверительного интервала с уровнем доверия, скажем, 95% состоит в следующем. Если провести очень большое количество независимых экспериментов с аналогичным построением доверительного интервала, то в 95% экспериментов доверительный интервал будет содержать оцениваемый параметр Примеры использования Массовая медицинская диагностика (скрининг) В медицинской практике есть существенное различие между скринингом и тестированием:
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии. [4] Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов. Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире. [5] Самый низкий уровень наблюдается в Нидерландах, 1%. [6] Медицинское тестирование Ошибки в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.017 с.) |


 :
: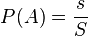

 — количество наблюдений, а
— количество наблюдений, а  — количество наступлений события
— количество наступлений события  .
. (тем более близкую, чем больше наблюдений). Собственно, в этом заключается исходный смысл понятия вероятности. В основе лежит объективистский взгляд на явления природы. Ниже будут рассмотрены так называемые законы больших чисел, которые дают теоретическую основу (в рамках излагаемого ниже современного аксиоматического подхода) в том числе для частотной оценки вероятности.
(тем более близкую, чем больше наблюдений). Собственно, в этом заключается исходный смысл понятия вероятности. В основе лежит объективистский взгляд на явления природы. Ниже будут рассмотрены так называемые законы больших чисел, которые дают теоретическую основу (в рамках излагаемого ниже современного аксиоматического подхода) в том числе для частотной оценки вероятности. . Подмножества этого пространства интерпретируются как случайные события. Объединение (сумма) некоторых подмножеств (событий) интерпретируется как событие, заключающееся в наступлении хотя бы одного из этих событий. Пересечение (произведение) подмножеств (событий) интерпретируется как событие, заключающееся в наступлении всех этих событий. Непересекающиеся множества интерпретируются как несовместные события (их совместное наступление невозможно). Соответственно, пустое множество означает невозможное событие.
. Подмножества этого пространства интерпретируются как случайные события. Объединение (сумма) некоторых подмножеств (событий) интерпретируется как событие, заключающееся в наступлении хотя бы одного из этих событий. Пересечение (произведение) подмножеств (событий) интерпретируется как событие, заключающееся в наступлении всех этих событий. Непересекающиеся множества интерпретируются как несовместные события (их совместное наступление невозможно). Соответственно, пустое множество означает невозможное событие. , заданная на множестве событий, обладающая следующими свойствами:
, заданная на множестве событий, обладающая следующими свойствами: ,
, при
при  , то
, то  .
.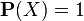 ,
, подмножеств [6]. Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность
подмножеств [6]. Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность  — то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера — называется вероятностным пространством.
— то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера — называется вероятностным пространством. ) равна нулю:
) равна нулю:
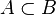 , то есть наступление события A влечёт также наступление события B, то:
, то есть наступление события A влечёт также наступление события B, то:
 , возможно, «содержит» кроме события
, возможно, «содержит» кроме события 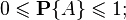
 .
. , где
, где 
 , противоположного событию
, противоположного событию 

 . Отсюда учитывая аддитивность вероятности для непересекающихся множеств и формулу для вероятности разности (см. свойство 4) множеств, получаем требуемое свойство.
. Отсюда учитывая аддитивность вероятности для непересекающихся множеств и формулу для вероятности разности (см. свойство 4) множеств, получаем требуемое свойство. . Наиболее просто вывести формулу определения условной вероятности исходя из классического определения вероятности. Для данных двух событий
. Наиболее просто вывести формулу определения условной вероятности исходя из классического определения вероятности. Для данных двух событий 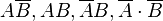 , которые исчерпывают все возможные варианты исходов (такой набор событий называют полным — см. ниже). Общее количество равновозможных исходов равно
, которые исчерпывают все возможные варианты исходов (такой набор событий называют полным — см. ниже). Общее количество равновозможных исходов равно  , что эквивалентно событию
, что эквивалентно событию  . Из этих исходов событию
. Из этих исходов событию  . Количество соответствующих исходов обозначим
. Количество соответствующих исходов обозначим  . Тогда согласно классическому определению вероятности вероятность события
. Тогда согласно классическому определению вероятности вероятность события  , разделив числитель и знаменатель на общее количество равновозможных исходов
, разделив числитель и знаменатель на общее количество равновозможных исходов 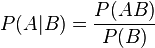 .
. .
. , отсюда следует формула Байеса:
, отсюда следует формула Байеса:
 , откуда следует, что для независимых событий выполняется равенство
, откуда следует, что для независимых событий выполняется равенство
 их независимость в совокупности означает, что вероятность их совместного наступления равна произведению их вероятностей:
их независимость в совокупности означает, что вероятность их совместного наступления равна произведению их вероятностей:

 и
и  с вероятностями
с вероятностями  соответственно. Таким образом:
соответственно. Таким образом: ,
,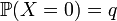 .
. соответствует «успеху», а событие
соответствует «успеху», а событие  — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
— «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.







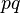

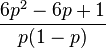

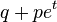

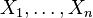 — конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром
— конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром 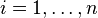 величина
величина  принимает значения
принимает значения  соответственно. Тогда случайная величина
соответственно. Тогда случайная величина
 .
. обычно интерпретируют как число успехов в серии из
обычно интерпретируют как число успехов в серии из 

 ,
, обозначает наибольшее целое, не превосходящее число
обозначает наибольшее целое, не превосходящее число 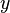 , или в виде неполной бета-функции:
, или в виде неполной бета-функции: .
. ,
, ,
, ,
,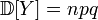 .
. и определим дискретное распределение, задаваемое следующей функцией вероятности:
и определим дискретное распределение, задаваемое следующей функцией вероятности: ,
, обозначает факториал числа
обозначает факториал числа 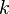 ,
, — основание натурального логарифма.
— основание натурального логарифма.  , записывается:
, записывается:  .
. ,
, ,
,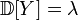 .
. ,
,
 (задающей вероятностное распределение
(задающей вероятностное распределение 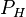 ) состоит в следующем. Выбирается событие
) состоит в следующем. Выбирается событие  (называемое статистическим критерием), которое (по каким-либо соображениям) «почти несовместимо» с гипотезой
(называемое статистическим критерием), которое (по каким-либо соображениям) «почти несовместимо» с гипотезой  события
события  не превышает какого-то малого (по сравнению с единицей) числа
не превышает какого-то малого (по сравнению с единицей) числа  , называемого уровнем значимости:
, называемого уровнем значимости:  . Затем проводится опыт. Если событие
. Затем проводится опыт. Если событие  полностью или частично неизвестно. Тогда любое утверждение, относительно
полностью или частично неизвестно. Тогда любое утверждение, относительно  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них: , где
, где  какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.  , где
, где 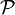 — семейство распределений, называется сложной.
— семейство распределений, называется сложной.  . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей или альтернативной.
, называемая конкурирующей или альтернативной. фиксированного объема
фиксированного объема  для распределения
для распределения  , где
, где  находят из условий
находят из условий  .
. , где
, где  находят из условия
находят из условия  .
. , где
, где 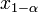 находят из условия
находят из условия  .
. из неизвестного совместного распределения
из неизвестного совместного распределения  , и поставлена бинарная задача проверки статистических гипотез:
, и поставлена бинарная задача проверки статистических гипотез:
 ,
, одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации: соответствует гипотезе
соответствует гипотезе  .
.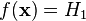 .
.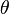 распределения случайной величины
распределения случайной величины  , называется интервал с границами
, называется интервал с границами  и
и  , которые являются реализациями случайных величин
, которые являются реализациями случайных величин  и
и  , таких, что
, таких, что .
. и
и  называются доверительными пределами.
называются доверительными пределами. ), а в оставшихся 5% экспериментов доверительный интервал не будет содержать
), а в оставшихся 5% экспериментов доверительный интервал не будет содержать 


