
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение баз данных. Текстографические и фактографические базы данных. Реляционные базы данных. Транзакции, откаты транзакций.Содержание книги
Поиск на нашем сайте
Математические модели. Детерминированные и стохастические динамические модели. Критерии адекватности моделей. Математические модели. Детерминированные и стохастические динамические модели. Критерии адекватности моделей. Математи́ческая моде́ль — математическоепредставлениереальности, один из вариантов модели, как системы, исследование которой позволяет получать информацию о некоторой другой системе. Процесс построения и изучения математических моделей называется математическим моделированием. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект исследования его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования Определения Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты. По Ляпунову, математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определенных отношениях и дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте. В других вариантах, математическая модель определяется как объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинал, как «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям», как систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого, исследование которых средствами математики должно ответить на поставленные вопросы о свойствах некоторой совокупности свойств объекта реального мира, как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе [6]. Классификация моделей Формальная классификация моделей Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий:
и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д. Динамическая модель — теоретическая конструкция (модель), описывающая изменение (динамику) состояний объекта. Динамическая модель может включать в себя описание этапов или фаз или диаграмму состояний подсистем. Часто имеет математическое выражение и используется главным образом в общественных науках (например, в социологии), имеющих дело с динамическими системами, однако современная парадигма науки способствует тому, что данная модель также имеет широкое распространение во всех без исключения науках, в том числе в естественных и технических. Динамическая модель описывает систему с различными аккумуляторами энергии, представляемыми в форме математических операций суммирования, интегрирования и дифференцирования. Например, потенциальная и кинетическая энергия механического движения массивного объекта. Такие модели в теории автоматического управления строятся в виде передаточных функций. Математическая модель, в которой в той или иной форме раскрываются причинно-следственные связи, определяющие процесс перехода системы из одного состояния в другое, называется динамической моделью. Характеристики вероятностных (иными словами, стохастических) моделей случайным образом распределяются в пространстве или меняются во времени. Это является следствием как случайного распределения свойств материалов, геометрических размеров и форм объекта, так и случайного характера воздействия внешних нагрузок и условий. Характеристики детерминированных моделей заранее известны и точно предсказуемы. Адекватность модели — совпадение свойств (функций/параметров/характеристик и т. п.) модели и соответствующих свойств моделируемого объекта. Адекватностью называется совпадение модели моделируемой системы в отношении цели моделирования. Оценка адекватности модели — проверка соответствия модели реальной системе. Оценка адекватности модели реальному объекту оценивается по близости результатов расчетов экспериментальным данным. Два основных подхода к оценке адекватности: 1) по средним значениям откликов модели и системы Проверяется гипотеза о близости средних значений каждой n-й компоненты откликов модели Yn известным средним значениям n-й компоненты откликов реальной систем. 2) по дисперсиям отклонений откликов модели от среднего значения откликов систем Сравнение дисперсии проводят с помощью критерия F (проверяют гипотезы о согласованности), с помощью критерия согласия?2 (при больших выборках, п>100), критерия Колмогорова- Смирнова (при малых выборках, известны средняя и дисперсия совокупности), Кохрена и др. Пример модели «Система хищник-жертва» Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры — Лотки ответа не дает: здесь требуются дополнительные исследования.
билет №_18_
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.203.195 (0.008 с.) |

 , число лис
, число лис 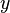 . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерры:
. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерры:



