Сила связи Направление связи

прямая (+) обратная (-)

Сильная от + 1 до +0,7 от - 1 до - 0,7

Средняя от + 0,699 до + 0,3 от - 0,699 до - 0,3

Слабая от + 0,299 до 0 от - 0,299 до 0

Метод корреляционной адаптометрии.

В основу метода положен анализ парной корреляции для всех показателей. Метод позволяет определить вклад каждой компоненты (показателя) в общую

дисперсию корреляционной матрицы и охарактеризовать различные

аспекты взаимосвязей в множестве переменных. Учитываются только

достоверные коэффициенты корреляции, при r > 0,05. Основная идея

метода – это демонстрация положения о том, что информационные

взаимоотношения как внутри отдельных функциональных систем, так

и в межсистемных связях в целом организме весьма чувствительны к

различным энергоинформационным внешним воздействиям.

Для корреляционного анализа используются несколько показателей состояния здоровья.

Статистическая обработка данных проводится с помощью

методов математической статистики (анализ значимости различий с

помощью t-критерия Стьюдента, корреляционный анализ).

Количество достоверных корреляционных связей определялось в

общем числе рассмотренных коэффициентов корреляции и степени

выраженности этих связей. Степень скоррелированности

параметров состояния здоровья оценивается с помощью веса

корреляционного графа, рассчитываемого как сумма весов его ребер

(сумма соответствующих коэффициентов корреляции):

 

 

 

где rij - коэффициент корреляции между i - м и j -м показателями, α

– определяется уровнем достоверности rij.

Чем выше величина корреляций, тем меньше существенных

факторов. В предельном случае, когда модуль всех коэффициентов

корреляции стремится к 1, все определяется одним фактором, все

параметры являются линейными функциями одной величины.

 

билет №_15_

Операционные системы: состав и назначение. Супервизор, утилиты. Система прерываний и приоритетов программ.

Прогнозирование по методу многомерной линейной регрессии. ROC-кривые.

Прогнозирование по методу многомерной линейной регрессии. ROC-кривые.

Можно считать, что прогнозирование является чуть ли не основной целью и задачей большого числа специалистов, занимающихся анализом данных. Современные методы статистического прогнозирования позволяют с высокой точностью прогнозировать практически все возможные показатели.

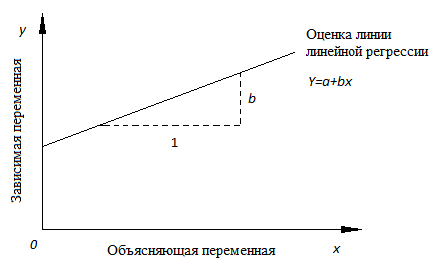
При анализе временных рядов можно выделить две основные цели:

·определение природы временного ряда

·прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям)

Однако надо помнить, что не существует универсальных методов прогнозирования на все случаи жизни. Выбор метода прогнозирования и его эффективность зависят от многих условий, и в частности от требуемой длины или времени прогнозирования.

По времени прогнозирования различают краткосрочный, среднесрочный и долгосрочный прогноз.

Краткосрочный прогноз характеризует собой прогноз «на завтра», то есть прогноз на несколько шагов вперед. Для него применяют практически все известные методы: экспоненциальное сглаживание, АРПСС (ARIMA) и нейронные сети.

Среднесрочный прогноз – это обычно прогноз на один или на половину сезонного цикла. Для него используют АРПСС и экспоненциальное сглаживание, которые позволяют отслеживать качество прогноза в зависимости от срока прогноза.

А при построении долгосрочного прогноза стандартные статистические методы прогнозирования практически не используют, и требуется использование комплексных подходов. Например, использование нейронных сетей или регрессионных моделей.

Что такое регрессия?

Рассмотрим две непрерывные переменные x=(x₁, x₂,.., x_n), y=(y₁, y₂,..., y_n).

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова "регрессия" исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей "регрессировал" и "двигался вспять" к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

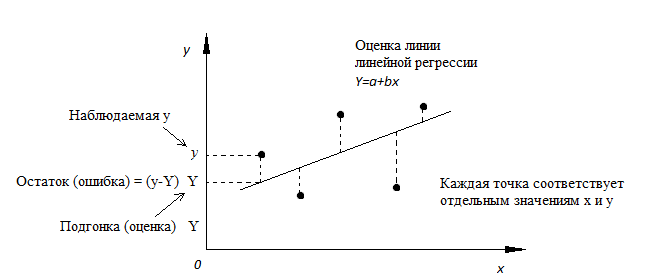
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β, которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.