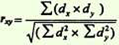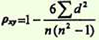Оценка уровня силы корреляционной связи между несколькими случайными величинами. Корреляционная адаптометрия.

Оценка уровня силы корреляционной связи между несколькими случайными величинами. Корреляционная адаптометрия.

Корреляционная связь

такая связь, при которой каждому определенному значению одного

признака соответствует несколько значений другого взаимосвязанного с ним

признака (связь между ростом и массой тела человека; связь между

температурой тела и частотой пульса и др.). Корреляционная связь

характерна для медико-биологических процессов.

Практическое значение установления корреляционной связи.

Выявление причинно-следственной между факторными и

результативными признаками (при оценке физического развития, для

определения связи между условиями труда, быта и состоянием здоровья, при

определении зависимости частоты случаев болезни от возраста, стажа,

наличия производственных вредностей и др.)

Зависимость параллельных изменений нескольких признаков от какой-

то третьей величины. Например, под воздействием высокой температуры в

цехе происходят изменения кровяного давления, вязкости крови, частоты

пульса и др.

Величина, характеризующая направление и силу связи между

Признаками.

Коэффициент корреляции, который одним числом дает представление о

направлении и силе связи между признаками (явлениями), пределы его

колебаний от 0 до ± 1

Способы представления корреляционной связи

o график (диаграмма рассеяния)

o коэффициент корреляции

Направление корреляционной связи

o прямая

o oбратная

Сила корреляционной связи

o сильная: ±0,7 до ±1

o средняя: ±0,3 до ±0,699

o слабая: 0 до ±0,299

Методы определения коэффициента корреляции и формулы

o метод квадратов (метод Пирсона)

o ранговый метод (метод Спирмена)

Методические требования к использованию коэффициента

Корреляции

o измерение связи возможно только в качественно однородных

совокупностях (например, измерение связи между ростом и весом в

совокупностях, однородных по полу и возрасту)

o расчет может производиться с использованием абсолютных или

производных величин

o для вычисления коэффициента корреляции используются не

сгруппированные вариационные ряды (это требование применяется только

при вычислении коэффициента корреляции по методу квадратов)

o число наблюдений менее 30

Рекомендации по применению метода ранговой корреляции (метод

Спирмена)

o когда нет необходимости в точном установлении силы связи, а

достаточно ориентировочных данных

o когда признаки представлены не только количественными, но и

атрибутивными значениями

o когда ряды распределения признаков имеют открытые варианты

(например, стаж работы до 1 года и др.)

Рекомендации к применению метода квадратов (метод Пирсона)

o когда требуется точное установление силы связи между

признаками

o когда признаки имеют только количественное выражение

Методика и порядок вычисления коэффициента корреляции

Метод квадратов

o построить вариационные ряды для каждого из сопоставляемых

признаков, обозначив первый и второй ряд чисел соответственно х и у;

o определить для каждого вариационного ряда средние значения

(М1 и М2);

o найти отклонения (dх и dy) каждого числового значения от

среднего значения своего вариационного ряда;

o полученные отклонения перемножить (dx X dy)

o каждое отклонение возвести в квадрат и суммировать по

каждому ряду (Σ dx^2 и dy^2)

o подставить полученные значения в формулу расчета

коэффициента корреляции:

 

 

Ранговый метод

o составить два ряда из парных сопоставляемых признаков,

обозначив первый и второй ряд соответственно х и у. При этом представить

первый ряд признака в убывающем или возрастающем порядке, а числовые

значения второго ряда расположить напротив тех значений первого ряда,

которым они соответствуют

o величину признака в каждом из сравниваемых рядов заменить

порядковым номером (рангом). Рангами, или номерами, обозначают места

показателей (значения) первого и второго рядов. При этом числовым

значениям второго признака ранги должны присваиваться в том же порядке,

какой был принят при раздаче их величинам первого признака. При

одинаковых величинах признака в ряду ранги следует определять как среднее

число из суммы порядковых номеров этих величин

o определить разность рангов между х и у (d): d = х — у

o возвести полученную разность рангов в квадрат (d^2)

o получить сумму квадратов разности (Σ d^2) и подставить

полученные значения в формулу:

 

 

Схема оценки корреляционной связи по коэффициенту

Корреляции