
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели эпидемического процесса.Содержание книги
Поиск на нашем сайте
Математической моделью называют абстрактную модель, в которой реальные объекты исследования заменяются идеальными и описываются при помощи математических соотноше- ний или различных алгоритмических схем. Моделирование следует рассматривать как важнейший инструмент познания эпидемического процесса. Широкое использование терминов «модель», «математическая модель» и самих моделей в эпидемиологии знаменует шаг вперед по сравнению с классическими методологическими установками. Моделирование эпидемического процесса имеет свою историю, причем главные ее страницы связаны с математическими моделями. Математическое моделирование в эпидемиологии - это формальное описание основных элементов механизма эпидемического процесса с помощью системы соотношений, формул, функций, уравнений и др. В зависимости от того, насколько глубоко описываемые в математических терминах элементы (факторы, показатели) характеризуют эпидемический процесс, различают несколько классов моделирования: 1) формальную апроксимацию (приближение), состоящую в перенесении знаний математического описания внешне подобных явлений из других областей (например, волновых колебаний) на эпидемический процесс; 2) формальную экстраполяцию (в основном кривых заболеваемости), дающую удовлетворительные результаты лишь в том случае, если факторы, формирующие рассматриваемый эпидемический процесс, примерно постоянны; 3) содержательное моделирование эпидемического процесса с дискретным или непрерывным течением. Каждый из этих классов моделирования оперирует своим специфическим набором математических средств, имеющих определенные ограничения и показания к применению. В то же время модели, относящиеся к одному классу, обеспечивают определенный уровень отдачи при исследовании эпидемического процесса. Следовательно, между задачей и способом моделирования имеется тесная связь. В эпидемиологии моделирование применяется в исследовательских целях, для прогнозирования характера эпидемического процесса и определения стратегии служб здравоохранения. Познавательная роль моделей определяется их сущностью, предполагающей выявление взаимосвязей многочисленных параметров эпидемического процесса. Хорошо организованная математическая модель дисциплинирует исследовательскую работу, систематизирует научные знания и нередко приводит к появлению новых идей. Она позволяет судить о числе контактов, определять степень риска инфицирования и заболевания, исследовать особенности возрастного и территориального распределения заболеваемости. Не менее важной функцией модели является описание многолетней динамики заболеваемости, включая сезонные циклы, что открывает возможность прогнозирования тенденций и уровней развития основных показателей эпидемического процесса. Разумное использование методов математического моделирования эпидемического процесса может быть чрезвычайно полезно также при планировании профилактических и противоэпидемических мероприятий, для выбора оптимальных путей борьбы с эпидемическим распространением заболеваний. При построении эпидемиологической модели различают несколько этапов: Большинство моделей сконструировано и применено с целью краткосрочного прогнозирования заболеваемости, что, по всей вероятности, диктуется потребностями противоэпидемической службы для подготовки и своевременной реализации в практических условиях эффективных профилактических, противоэпидемических и лечебных мероприятий. Исследовательским задачам, соподчиненным с выбором оптимальной тактики борьбы с заболеваемостью, посвящено лишь незначительное число моделей. За многие годы существования человечества огромное число людей погибло от различных эпидемий. Чума, холера, грипп и др. нередко поражали значительные массы людей. Для того, чтобы иметь возможность бороться с эпидемиями, т.е. своевременно применять те или иные медицинские мероприятия (карантины, вакцинации и т.п.),необходимо уметь сравнивать эффективность этих мероприятий. Сравнить же их можно лишь в том случае, если есть возможность предсказать, как при том или ином мероприятии будет меняться ход эпидемии, т.е. как будет меняться число заболевших. Отсюда возникает необходимость в построении модели, которая могла бы служить целям прогноза. Для простоты рассмотрим естественный ход эпидемии без какого-либо вмешательства и попробуем спрогнозировать последствия. Так как нашей целью является лишь создание иллюстративной модели, то здесь мы абстрагируемся от очень многих факторов (условия размножения бактериальных клеток, степень восприимчивости к инфекции отдельных людей, вероятность встречи носителя инфекции со здоровым человеком и т.д.)
Итак, пусть имеется N здоровых людей, и в момент времени t=0 в эту группу попадает один заболевший человек – источник инфекции. Будем предполагать, что никакого удаления заболевших из группы не происходит. Считаем также, что человек становится источником инфекции сразу же после того, как он сам заразится. Допустим в некоторый момент времени t X(t) – число источников инфекции, Y(t) – число людей, могущих заболеть, Тогда имеем X(t)+Y(t)=N+1 в любой момент времени. При t=0 выполняется условие X(0)=1 Количество новых больных dX, появившихся за промежуток времени dt, будет пропорционально числу встреч здоровых и заболевших людей, т.е. произведению величин XY. Следовательно, можно записать
где a – коэффициент пропорциональности. Полученное дифференциальное уравнение вместе с условием X(0)=1 определяет функцию X(t), т.е. численность заболевших в момент времени t. Найдем общее решение, предварительно разделив переменные.
Чтобы взять первый интеграл, разделим числитель и знаменатель дроби на Заменим под интегралом переменную, получим
После интегрирования имеем
С учетом того, что
Так как при t=0 значение X(t)=1, то для определения величины С имеем уравнение
Окончательно получаем
Итак, мы знаем число заболевших как функцию времени. Проанализируем полученную формулу. При возрастании t знаменатель дроби убывает, т. е. X(t) увеличивается. Это соответствует нашим представлениям, так как, согласно им, число заболевших может только увеличиваться. Интересно выяснить, как меняется скорость увеличения числа больных. Для решения этого вопроса нужно изучить величину Дифференцируя, получаем
Числитель дроби обращается в нуль при Таким образом, когда Следовательно, функция Этот результат хорошо согласуется с экспериментальными данными, так как известно, что в начале эпидемии число заболевших резко растет, а впоследствии скорость распространения инфекции снижается.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 2847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.211 (0.008 с.) |

 или
или  ,
,
 и введем новую переменную
и введем новую переменную  , тогда
, тогда 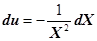 , и отсюда
, и отсюда  .
.
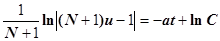 , и, следовательно
, и, следовательно 

 , откуда C=N
, откуда C=N
 .
.
 .
. , величина
, величина  , а когда
, а когда  , величина
, величина  .
. - скорость возрастания числа заболевших – растет вплоть до момента
- скорость возрастания числа заболевших – растет вплоть до момента 


