
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерфейсы. Определение интерфейса. Последовательные и параллельные интерфейсы. Внутренние и внешние интерфейсы современных персональных компьютеров.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Интервальные оценки параметров. Определение достоверности различия средних и дисперсий. Расчет доверительных интервалов для процентилей. Интервальные оценки параметров. Определение достоверности различия средних и дисперсий. Расчет доверительных интервалов для процентилей. Задача интервального оценивания параметров Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Т, получила название методов интервального оценивания. Чтобы дать представление о точности и надежности оценки Пусть для параметра
Тогда диапазон практически возможных значений ошибки, возникающей при замене Перепишем (14.3.1) в виде:
Равенство (14.3.2) означает, что с вероятностью
При этом необходимо отметить одно обстоятельство. Ранее мы неоднократно рассматривали вероятность попадания случайной величины в заданный неслучайный интервал. Здесь дело обстоит иначе: величина
Рис. 14.3.1. Вероятность Дадим еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра Перейдем к вопросу о нахождении доверительных границ Пусть для параметра
Затруднение состоит в том, что закон распределения оценки Чтобы обойти это затруднение, можно применить следующий грубо приближенный прием: заменить в выражении для Определение достоверности различия средних и дисперсий.
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

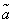 , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями. получена из опыта несмещенная оценка
получена из опыта несмещенная оценка  (например,
(например, 
 или
или  ) такую, что событие с вероятностью
) такую, что событие с вероятностью  , для которого
, для которого . (14.3.1)
. (14.3.1) ; большие по абсолютной величине ошибки будут появляться только с малой вероятностью
; большие по абсолютной величине ошибки будут появляться только с малой вероятностью  .
. . (14.3.2)
. (14.3.2) . (14.3.3)
. (14.3.3)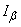 . Случайно его положение на оси абсцисс, определяемое его центром
. Случайно его положение на оси абсцисс, определяемое его центром 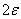 , так как величина
, так как величина 
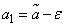 и
и  называются доверительными границами.
называются доверительными границами. , нужно признать противоречащими опытным данным, а те, для которых
, нужно признать противоречащими опытным данным, а те, для которых  , - совместимыми с ними.
, - совместимыми с ними. и
и 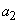 .
.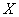 и, следовательно, от его неизвестных параметров (в частности, и от самого параметра
и, следовательно, от его неизвестных параметров (в частности, и от самого параметра  (порядка
(порядка  ) этот прием обычно дает удовлетворительные по точности результаты.
) этот прием обычно дает удовлетворительные по точности результаты.


