
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события. Классическое определение вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Понятие о случайном событии. Опыт, эксперимент, наблюдение явления называют испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенным на каждую грань числом очков — от одного до шести). Результат, исход испытания называется событием. Событиями являются: выпадение герба или цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д. Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. Пример1. Испытание: однократное бросание игральной кости. Событие А — появление четырех очков, событие В — появление четного числа очков. События А и В совместимые. Определение 2. Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании. Пример 2. Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В— выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого. Несовместимость более чем двух событий в данном испытании означает их попарную несовместимость. Пример 3. Испытание: однократное бросание игральной кости. Пусть события А1, Аг, А3, А Определение 3. Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через П р и м е р 4. Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В— выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они_и появление одного из них исключает появление другого, т. е. А = Определение 4. Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти. Пример 5. Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие. Заметим, что достоверное и невозможное события в данном испытании являются противоположными. Определение 5. Событие А называется случайным, если оно объективно может наступить или не наступить в данном испытании. Пример 6. Событие А6 — выпадение шести очков при бросании игральной кости — случайное. Оно может наступить, но может и не наступить в данном испытании. Пример 7. Событие А98 — прорастание девяноста восьми зерен пшеницы из ста — случайное. Это событие может наступить, но, может быть, прорастет зерен больше или меньше. Алгебра событий. Определение 1. Суммой событий A и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С=А+В, состоящее в попадании в мишень по крайней мере одним стрелком. Аналогично суммой конечного числа событий А Из определения 1 непосредственно следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А+А=А (а не 2А, как в алгебре). Определение 2. Произведением событий А и В называется событие С=АВ, состоящее в том, что в результате испытания произошли и событие А, и событие В. Аналогично произведением конечного числа событий А В условиях предыдущего примера произведением событий А и В будет событие С=АВ, состоящее в попадании в мишень двумя стрелками. Из определения 2 непосредственно следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако АА = А (а не Аг). 3. Классическое определение вероятности. Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания. Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них. Примеры полных групп событий — выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости. Рассмотрим полную группу попарно несовместимых событий U1,U2,..., Un,, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий U Определение 2. События U Пример 1. Вернемся к опыту с подбрасыванием игральной кости. Пусть U Определение 3. Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В. Пример 2. Пусть при бросании игральной кости события U2, U4 и U 6 — появление соответственно двух, четырех и шести очков, а А — событие, состоящее в появлении четного числа очков; события U2, U4 и U 6 благоприятствуют событию А. Определение 4 (классическое определение вероятности). Вероятностью Р(А) события А называется отношение т/п числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Р(А) = т/п. Пример 3. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба — и событие В— выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь п = 2. Событию А благоприятствует лишь одно событие—само А, т.е. здесь m=1. Поэтому Р(А) = П р и м ер 4. Очевидно, что при одном бросании игральной кости (вероятность выпадения какой-либо цифры от 1 до 6 будет равна P(U Пример 5. Найдем вероятность того, что при однократном бросании игральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятствующих элементарных событии 3 (выпадение 2, 4 и 6). Поэтому
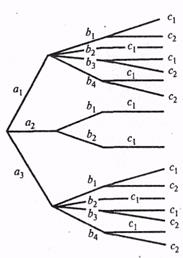
Пример 6. При составлении команды космического корабля возникает вопрос о психологической совместимости отдельных членов экипажа. Допустим, что надо составить команду из трех человек: командира, инженера и врача. На место командира есть три кандидата: а1, а2 , a 3; на место инженера — четыре кандидата: Ь Представим все варианты команды, при которых члены экипажа совместимы друг с другом в виде «дерева» (рис. 1). Число ветвей этого дерева, т. е. исходов, благоприятствующих событию А,равно 16, а общее число возможных комбинаций по правилу произведения равно 4 Задача (Вероятности рождения мальчиков и девочек). Будем предполагать, что случаи рождения мальчика Пусть в семье двое детей. Какова вероятность, что оба ребенка — мальчики? Если известно, что один мальчик, какова вероятность, что оба ребенка — мальчики? На первый вопрос ответить нетрудно. Имеется четыре равно-возможных исхода: ММ, МД, ДМ, ДД (М— мальчик, Д— девочка). Исходы МД и ДМ различны, так как в первом из них сначала родился мальчик, а потом девочка, во втором — наоборот. Из этих четырех исходов только один ММ благоприятствует нашему событию. Отсюда следует, что Р(ММ) = Если дополнительно известно, что один ребенок — мальчик, то событие ДД исключается. Из трех равновозможных событий ММ, МД, ДМ по-прежнему только одно ММ благоприятствует желаемому исходу. Поэтому Р(ММ) = Если известно, что старший ребенок— мальчик, то исключаются исходы ДМ и ДД. В этом случае Р(ММ) = Из приведенного классического определения вероятности вытекают следующие ее свойства: 1. Вероятность достоверного события равна единице. Р(А) = т/п = п/п = 1. 2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. т = 0, откуда Р(А) = т/п = 0/п = 0. 3. Вероятность случайного события есть положительное число, Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0<т<п и, значит, 0< т / п <1. Следовательно, 0<Р(А)<1. Таким образом, вероятность любого события удовлетворяет двойному неравенству 0 Замечание. Из определения вероятности следует, что элементарные события являются равновероятными, т. е. обладают одной и той же вероятностью.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.225 (0.007 с.) |

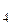 , А5, А 6 — соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.
, А5, А 6 — соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.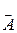 .
. или
или  , А2,..., Ак называется событие А = А
, А2,..., Ак называется событие А = А  (і =1,..., к).
(і =1,..., к). называется событие А = А
называется событие А = А  U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называют элементарными событиями.
U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называют элементарными событиями.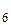 , образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 U2,..., U
, образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 U2,..., U  .
.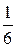 , i =l, 2,..., 6.
, i =l, 2,..., 6.
 , b
, b  3
3 

 и девочки — равновозможные события.
и девочки — равновозможные события.

 .
. Р(А)
Р(А) 


