
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление вероятности событияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Время проведения – 2 часа. Цель работы: вычисление вероятностей событий по классической формуле определения вероятности; вычисление вероятностей совместных событий; определение вероятности по формулам суммы и произведения. Вопросы для подготовки к работе: 1. Понятие события; 2. Понятие случайного события; 3. Понятие достоверного события; 4. Понятие невозможного события; 5. Понятие противоположного события; 6. Понятие несовместного события; 7. Понятие совместного события; 8. Понятие разности событий; 9. Понятие независимых событий; 10. Понятие зависимых событий; 11. Понятие условной вероятности; 12. Классическое определение вероятности; 13. Вероятность суммы несовместных событий; 14. Вероятность суммы совместных событий; 15. Вероятность произведения зависимых событий; 16. Вероятность произведения независимых событий; Содержание работы: 1. Вычисление вероятности событий по классической формуле определения вероятности; 2. Определение вероятности по формуле суммы; 3. Определение вероятности по формуле произведения. Порядок выполнения задания: Вероятность события характеризует степень объективной возможности наступления этого события. Если, в частности, множество состоит из равновозможных элементарных событий, то вероятность Пример: В ящике пять пронумерованных шаров с номерами от 1 до 5. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 5? Решение: Так как номер шара не превышает 5, то число случаев благоприятных событию Ответ: Пример: Бросают две игральные кости. Какое событие более вероятно: сумма очков на выпавших гранях равна 11 или сумма очков на выпавших гранях равна 4? Решение: Поставим в соответствие исходу эксперимента упорядоченную пару чисел Пространство всех элементарных событий состоит из множества пар Имеем, Ответ: событие Теорема сложения вероятностей: Вероятность суммы двух совместных событий Теорема умножения вероятностей: Вероятность произведения двух зависимых событий Обобщенная теорема умножения: Вероятность произведения событий, независимых в совокупности, равна произведению вероятностей этих событий. Пример: Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка – 0,75, для второго – 0,8, для третьего – 0,9. Найти вероятность того, что все три стрелка попадут в цель. Решение: Пусть событие Ответ: Пример: Идет бомбардировка трех складов боеприпасов. Сбрасывают одну бомбу. Вероятность попадания в первый склад равна 0,01; во второй 0,008; в третий 0,025. При попадании в любой из них взрываются все. Найти вероятность того, что склады будут взорваны. Решение: Событие Ответ: Пример: Имеется три ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными. Решение: Вероятность того, что из первого ящика вынута стандартная деталь (событие Вероятность того, что из второго ящика вынута стандартная деталь (событие Вероятность того, что из третьего ящика вынута стандартная деталь (событие Так как события Ответ: Пример: Бросают две монеты. Рассматриваются события Решение: Так как Ответ: Пример: Из 12 аппаратов четыре первого типа и восемь второго. Случайным образом из них выбирают три аппарата последовательно (без возвращения). Найти вероятность того, что при первом и третьем будут выбраны аппараты второго типа, а вторым – аппарат первого типа. Решение: Пусть Ответ:
Вариант 1 1. Подброшены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 7. 2. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет: а) не менее двух раз; б) менее двух раз 3. Имеются две одинаковые урны. В первой урне находятся 3 белых и 5 черных шаров, во второй – 3 белых и 7 черных шаров. Из одной наугад выбранной урны извлекается шар. Определить вероятность того, что шар черный. Вариант 2 1. Набирая номер телефона абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. 2. Пусть вероятность того, что наудачу взятая деталь нестандартная, равно 0,1. Найти вероятность того, что среди взятых наудачу 5 деталей не более двух нестандартных. 3. Имеются три одинаковые урны. В первой урне находятся 5 белых и 5 черных шаров, во второй – 3 белых и 2 черных, в третьей – 7 белых и 3 черных. Из одной наугад выбранной урны извлекают шар. Определить вероятность того, что шар будет белый. Практическая работа № 10 Операции над множествами Время проведения – 2 часа. Цель работы: формирование умений выполнять действия над множествами; Вопросы для подготовки к работе: 1. Понятие множества, подмножества; 2. Принадлежность элемента множеству; 3. Равенство множеств; 4. Пустое множество; 5. Конечное множество; 6. Бесконечное множество; 7. Дополнение множества; 8. Включение подмножества в множество; 9. Способы задания множеств; 10. Диаграмма Эйлера-Венна; 11. Операции над множествами. Содержание работы: 1. Задание множеств; 2. Выполнение операций над множествами. Порядок выполнения задания: При решении первого задания необходимо множество задать перечислением всех своих элементов – это один из способов задания множеств, если оно конечно. Пример: Множество Решение: Найдем множество действительных решений уравнения
Все корни уравнения действительные, то есть удовлетворяют условию Ответ: Пример: Множество Решение: Решим неравенство
Найдем корни квадратного трехчлена:
Решением неравенства Итак, согласно условию Ответ: Для выполнения второго, третьего заданий используются понятия объединения, пересечения, разности, равенства, дополнения множеств, диаграмма Эйлера-Венна. Пример: Даны множества Решение: Определим элементы множества Для построения диаграммы Венна рассмотрим, как связаны между собой множества
C
Определим элементы множества Строим диаграмму Венна:
C
Вариант 1 1. Множества задать перечислением всех своих элементов 1) 2) 2. Даны множества 3. Даны множества
Вариант 2 1. Множества задать перечислением всех своих элементов 1) 2) 2. Даны множества 3. Даны множества
ЛИТЕРАТУРА: Основные источники: 1. Богомолов Н. В., Самойленко П. И. Математика: Учебное пособие для техникумов, 7-е издание. - М.: Дрофа, 2010. – 400 с. 2. Богомолов Н.В. Сборник задач по математике: учеб. пособие для ссузов / Н.В. Богомолов.-М.: Дрофа, 2010. - 204 с. Дополнительные источники: 1. Мордкович А. Г. Алгебра и начала математического анализа. 10—11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. — 10-е изд., стер. — М.: Мнемозина, 2009. — 399 с. 2. Филимонова Е.В. Математика: Учебное пособие для средних специальных учебных заведений.- Ростов н/Д: Феникс, 2005.- 416с. (Серия «Среднее профессиональное образование»).
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 , где
, где  - число благоприятных исходов
- число благоприятных исходов  ,
,  - число всех всевозможных исходов (классическое определение вероятности).
- число всех всевозможных исходов (классическое определение вероятности). . Следовательно
. Следовательно  ., то есть событие
., то есть событие 
 , где
, где  - число очков, выпавших на первой кости, а
- число очков, выпавших на первой кости, а  - на второй.
- на второй. и
и  . Событию
. Событию  , состоящему в том, что сумма очков, выпавших на двух костях, равна 4, благоприятны три элементарных события, которым соответствуют
, состоящему в том, что сумма очков, выпавших на двух костях, равна 4, благоприятны три элементарных события, которым соответствуют  .
. , следовательно, событие
, следовательно, событие  . Вероятность суммы несовместных событий равна сумме их вероятностей, то есть
. Вероятность суммы несовместных событий равна сумме их вероятностей, то есть  . Эта теорема обобщается на случай произвольного числа попарно несовместных событий.
. Эта теорема обобщается на случай произвольного числа попарно несовместных событий. . Вероятность произведения двух независимых событий равна произведению вероятностей этих событий, то есть
. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий, то есть  .
. - третий стрелок попал в цель, тогда
- третий стрелок попал в цель, тогда 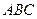 - все три стрелка попадут в цель.
- все три стрелка попадут в цель. 

 - попадание в первый склад,
- попадание в первый склад,  - попадание во второй склад,
- попадание во второй склад,  - попадание в третий склад, следовательно,
- попадание в третий склад, следовательно,  . Так как
. Так как  несовместны, то
несовместны, то 

 .
. .
.
 независимы, то искомая вероятность события
независимы, то искомая вероятность события 


 , или через противоположное событие
, или через противоположное событие
 - выбран третий аппарат. По классической формуле
- выбран третий аппарат. По классической формуле  определим
определим  , то есть первый аппарат второго типа,
, то есть первый аппарат второго типа,  , то есть второй аппарат первого типа, а всего аппаратов осталось 11,
, то есть второй аппарат первого типа, а всего аппаратов осталось 11,  , так как третий аппарат второго типа, а их осталось 7, и всего аппаратов 10.
, так как третий аппарат второго типа, а их осталось 7, и всего аппаратов 10. 

 задать перечислением всех своих элементов.
задать перечислением всех своих элементов.
 или
или 


 , следовательно
, следовательно 
 задать перечислением всех своих элементов.
задать перечислением всех своих элементов. методом интервалов
методом интервалов











 -1,5
-1,5
 , то есть
, то есть 
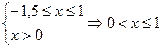 , отметим, что из данного промежутка действительным числам принадлежит только
, отметим, что из данного промежутка действительным числам принадлежит только  , следовательно
, следовательно  - множество из одного элемента.
- множество из одного элемента. . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна. . Элементы
. Элементы  и
и  одновременно принадлежат множеству
одновременно принадлежат множеству  . Аналогично
. Аналогично  . Таким образом, объединение
. Таким образом, объединение  .
.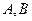 и
и 

 A B
A B

 X
X . Если отсюда исключить пять элементов множества
. Если отсюда исключить пять элементов множества  из двадцати одноИго элемента
из двадцати одноИго элемента  . Пересечение множеств
. Пересечение множеств  состоит из элементов
состоит из элементов  , то есть всех элементов множества
, то есть всех элементов множества  вычеркнем из множества
вычеркнем из множества  элементы
элементы  , принадлежащие
, принадлежащие  . Получим
. Получим  . В итоге
. В итоге  .
.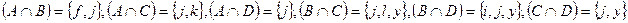



 A B
A B




 Y
Y

 D
D

 . Найдите множества
. Найдите множества  и
и  . Найдите множества
. Найдите множества 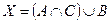 и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна.

 . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна. . Найдите множества
. Найдите множества  и
и  . Составьте диаграммы Венна.
. Составьте диаграммы Венна.


