
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиомы теории вероятностей. Свойства вероятности.Содержание книги
Поиск на нашем сайте
Аксиомы теории вероятностей. Свойства вероятности. Опр.: Под событием понимают любой факт, который может произойти в результате опыта или испытания. Опр.: Под опытом, или испытанием, понимается осуществление определённого комплекса условий. Опр.: Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Опр.: Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта. Событие называется невозможным, если оно не может произойти в условиях данного опыта. Опр.: Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Опр.: Под противоположным событием Опр.: Вероятностью события называется число, являющееся выражением меры объективной возможности появления события. Вероятность события Вероятность события Из формулы следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев: Аксиома 1. Каждому событию Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3. Вероятность невозможного события равна нулю. Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей. Свойства вероятности: 1. Если нет ни одного случая, благоприятствующего данному событию 2. Вероятность наступления противоположного события
где
3. Если событие A влечет за собой событие B, т.е. A ⊂ B, то вероятность события C, где C — разность событий B и A, определяется соотношением P(C) = P(B \ A) = P(B) − P(A). 4. Если событие A влечет за собой событие B, т.е. A ⊂ B, то вероятность события A не может быть больше вероятности события B, т.е. P(A) ≤ P(B). 5. Вероятность любого события заключена между нулем и единицей: 0 ≤ P(A) ≤ 1 6. Вероятность суммы любых двух событий равна сумме вероятностей этих событий минус вероятность их совместного появления: P(A + B) = P(A) + P(B) − P(AB). 7. Вероятность суммы событий не превосходит сумму вероятностей этих событий: P(A + B) ≤ P(A) + P(B).
Равномерный закон распределения
f(х)= при a<х<b,
0 при х≥b.
График функции f(x) изображен на рис. 1
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:
F(х)= 0 при х>b. Ее график изображен на рис. 2.
Аксиомы теории вероятностей. Свойства вероятности. Опр.: Под событием понимают любой факт, который может произойти в результате опыта или испытания. Опр.: Под опытом, или испытанием, понимается осуществление определённого комплекса условий. Опр.: Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Опр.: Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта. Событие называется невозможным, если оно не может произойти в условиях данного опыта. Опр.: Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться.
Опр.: Под противоположным событием Опр.: Вероятностью события называется число, являющееся выражением меры объективной возможности появления события. Вероятность события Вероятность события Из формулы следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев: Аксиома 1. Каждому событию Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3. Вероятность невозможного события равна нулю. Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей. Свойства вероятности: 1. Если нет ни одного случая, благоприятствующего данному событию 2. Вероятность наступления противоположного события
где
3. Если событие A влечет за собой событие B, т.е. A ⊂ B, то вероятность события C, где C — разность событий B и A, определяется соотношением P(C) = P(B \ A) = P(B) − P(A). 4. Если событие A влечет за собой событие B, т.е. A ⊂ B, то вероятность события A не может быть больше вероятности события B, т.е. P(A) ≤ P(B). 5. Вероятность любого события заключена между нулем и единицей: 0 ≤ P(A) ≤ 1 6. Вероятность суммы любых двух событий равна сумме вероятностей этих событий минус вероятность их совместного появления: P(A + B) = P(A) + P(B) − P(AB). 7. Вероятность суммы событий не превосходит сумму вероятностей этих событий: P(A + B) ≤ P(A) + P(B).
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1703; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.103.13 (0.008 с.) |

 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие 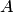 . Противоположные события несовместны и единственно возможны.
. Противоположные события несовместны и единственно возможны. .
.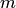 , благоприятствующих ему, из общего числа
, благоприятствующих ему, из общего числа  единственно возможных, равновозможных и несовместных случаев к числу
единственно возможных, равновозможных и несовместных случаев к числу 
 .
. и называемое его вероятностью.
и называемое его вероятностью. , так как в этом случае
, так как в этом случае 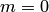 :
: 
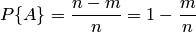
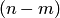 — число случаев, благоприятствующих появлению противоположного события
— число случаев, благоприятствующих появлению противоположного события 
 Опр.:Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е.
Опр.:Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е. 0 при х≤а,
0 при х≤а,

 (рис. 1) (рис.2)
(рис. 1) (рис.2) 0 при х≤а,
0 при х≤а, при a<х≤b,
при a<х≤b,


