
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднее квадратическое отклонение.Содержание книги
Поиск на нашем сайте
О п р е д е л е н и е. Средним квадратическим отклонением
Необходимость введения среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. Например, если возможные значения некоторой случайной величины измеряются в метрах, то еедисперсия измеряется в квадратных метрах. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, и используется среднее квадратическое отклонение. П р и м е р. Случайная величина X - число очков, выпавших при однократном бросании игральной кости. Определим o(X). Имеем: M(X) = l • D(X) = (1 - 3,5)2 • + (4 - 3,5)2 •
Понятие o моментах распределения. О п р е д е л е н и е 1. Начальным моментом порядка k случайной величины X называется математическое ожидание случайной величины Хk,где k -натуральное число: vk = M(Xk). Cледствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения: F(- 2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины Х (или ее плотностью вероятности, или ее плотностью распределения) называется функция f(x), равная производной интегральной функции f(x)=F’(x). Так как F(x) -неубывающая функция, то f(x) Из равенства (2.9) с учетом неравенства F(x+ P(x<X<x+ P(x<X<x+ (для малых Имеет место и следующая теорема. Теорема. Вероятность попадания непрерывной случайной величины Х в интервал (a;b) равна определенному интегралу от ее плотности вероятности, взятому в пределах от a до b: P(a<X<b)= Доказательство. Так как F(x)является первообразной для f(x), то на основании формулы Ньютона-Лейбница имеем
Теперь с учетом (2.9), (2.12), (2.14) получим искомое равенство. Из (2.13) следует, что геометрическая вероятность P(a<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности y=f(x) и отрезками прямых y = 0, x = a и x = b. Следствие. В частности, если f(x) - четная функция и концы интервала симметричны относительно начала координат, то P(-a<X<a)=P(
Действительно.
П р и м е р 1. Пусть задана плотность вероятности случайной величины X
Найдем вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу(0,5; 1). Согласно формуле (2.13), искомая вероятность P(0,5<X<1)=2 Заменяя в формуле (2.14) а на - F(x) - F(- F(x)= Выражение (2.16)позволяет найти интегральную функцию распределения F(x) по ее плотности вероятности. Заметим что формулы (2.16) и отмеченного следствия вытекает что
Пример 2. Пусть плотность вероятности случайной величины Х задана так: f(x)= Требуется найти коэффициент А, функцию распределения F(x) и вероятность попадания случайной величины Х в интервал (0; 1). Покажем, что M(X)=a, Введя новую переменную t по формуле (2.24), с учетом равенства(2.25) получим M(X)= Далее, а в соответствие с формулой (2.19) D(X)= Воспользовавшись подстановкой(2.24), получим: D(X)= Применяя здесь метод интегрирования по частям (t=u, te D(X)=- График функции (кривая Гаусса) имеет вид(рис 6). С учетом графика этой функции график функции (2.22) будет иметь вид (рис.7). Причем его максимальная ордината равна1/(
Нормальное распределение с параметрами а =0 и
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.006 с.) |

 (X) случайной величины X называется корень квадратный из ее дисперсии:
(X) случайной величины X называется корень квадратный из ее дисперсии:
 + 2 •
+ 2 • 
 2,92;
2,92;
 1,71.
1,71. )=
)=  F(x)=0; F(+
F(x)=0; F(+  F(x)=1
F(x)=1 0.
0. )-F(x)
)-F(x)  , и свойства 5(п.1) имеем
, и свойства 5(п.1) имеем F
F 

 , т.е. вероятность попадания случайной величины X в интервал (x; x+
, т.е. вероятность попадания случайной величины X в интервал (x; x+  (2.13)
(2.13) (2.14)
(2.14) <a)=2
<a)=2  (2.15).
(2.15).

 =0,75.
=0,75.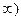 =
=  откуда в силу приведенного выше следствия (п.1)
откуда в силу приведенного выше следствия (п.1)
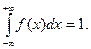
 (-
(- 
 или
или  = D(x) Согласно формуле(2.18), получаем M(X)=
= D(x) Согласно формуле(2.18), получаем M(X)= 
 dx.
dx. )e
)e 


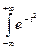 dt+
dt+ 
 dt=a-
dt=a-  e
e  =a.
=a. e-
e-  dx.
dx.


 ). Значит эта ордината убывает с возрастанием значения
). Значит эта ордината убывает с возрастанием значения 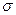 (кривая «растягивается» к оси Ох-рис.8) и возрастает
(кривая «растягивается» к оси Ох-рис.8) и возрастает 


 называется нормированным. Плотность вероятности в случае такого распределения оказывается равной
называется нормированным. Плотность вероятности в случае такого распределения оказывается равной



