
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценки математического ожидания и дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть закон распределения случайной величины X содержит неизвестный параметр
наблюдаемые значения случайной величины X, получаемые в результате n независимых опытов. Но, с другой стороны, результат можно представлять как набор n независимых случайных величин:
представляющих собой n независимых копий случайной величины X, именно Случайная величина
построенная на основе статистических данных называется оценкой (точечной оценкой) параметра 1. Несмещенность. Оценка
В противном случае (если Естественно в качестве оценки, т.е. приближенного значения неизвестного параметра, брать несмещенные оценки; в этом случае мы не делаем систематической ошибки в сторону завышения или занижения. 2. Состоятельность. Оценка
Состоятельность оценки означает, что при достаточно большом числе опытов n со сколько угодно большой достоверностью отклонение оценки от истинного значения параметра по модулю меньше любого заранее выбранного числа e > 0. 3. Эффективность. Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями. Чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной, т.е. чтобы выполнялось условие:
Оценка, обладающая свойством, называется эффективной, иначе, если при заданном объеме выборки имеет наименьшую дисперсию. Условия несмещенности, состоятельности и эффективности являются условиями доброкачественности оценки, что является необходимым при обработке статистических данных.
Точечные оценки математического ожидания Если рассматривается случайная величина В качестве оценок
Оценка математического ожидания (8.11) является состоятельной согласно закону больших чисел (теорема Чебышева):
Математическое ожидание случайной величины
Следовательно, оценка Дисперсия оценки математического ожидания:
Если случайная величина Математическое ожидание оценки дисперсии
В то же время
Так как
Таким образом, Из формулы (8.13) следует, что для получения несмещенной оценки
которая считается "лучшей" по сравнению с оценкой (8.12), хотя при больших
билет №_11_ Накопители на дискетах. Флешь-накопители и накопители на электронных картах. Накопители на оптических дисках. Общие принципы устройства, записи и хранения, технические характеристики. Центральная предельная теорема. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 . Требуется на основании опытных данных найти подходящую оценку для параметра
. Требуется на основании опытных данных найти подходящую оценку для параметра 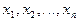
 ,
,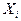 – случайная величина, представляющая собой результат i-го опыта, но имеющая тот же закон распределения, что исследуемая случайная величина X.
– случайная величина, представляющая собой результат i-го опыта, но имеющая тот же закон распределения, что исследуемая случайная величина X. ,
, является случайной величиной, закон распределения которой зависит, во-первых, от закона распределения случайной величины X, во-вторых, от числа опытов n. Для того чтобы оценка имела практическую ценность, она должна обладать следующими свойствами:
является случайной величиной, закон распределения которой зависит, во-первых, от закона распределения случайной величины X, во-вторых, от числа опытов n. Для того чтобы оценка имела практическую ценность, она должна обладать следующими свойствами: .
. ) оценка
) оценка  при
при 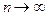 .
.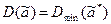 .
. , имеющая математическое ожидание
, имеющая математическое ожидание  и дисперсию
и дисперсию  , то оба эти параметра считаются неизвестными. Поэтому над случайной величиной
, то оба эти параметра считаются неизвестными. Поэтому над случайной величиной  производится
производится  независимых опытов, которые дают результаты:
независимых опытов, которые дают результаты:  . Необходимо найти состоятельные и несмещенные оценки неизвестных параметров
. Необходимо найти состоятельные и несмещенные оценки неизвестных параметров  и
и  и
и  обычно выбираются соответственно статистическое (выборочное) среднее значение и статистическая (выборочная) дисперсия:
обычно выбираются соответственно статистическое (выборочное) среднее значение и статистическая (выборочная) дисперсия: ; (8.11)
; (8.11) . (8.12)
. (8.12)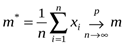 .
.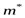
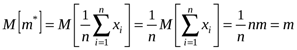 .
.
 .
.
 .
.
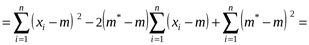

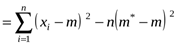 .
. , а
, а  , то получаем
, то получаем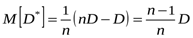 . (8.13)
. (8.13) – смещенная оценка, хотя является состоятельной и эффективной.
– смещенная оценка, хотя является состоятельной и эффективной. , (8.14)
, (8.14)


