
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии оценки качества модели регрессииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Качество математической модели регрессии можно оценить по нескольким критериям. Полученная математическая модель будет качественной в том случае, если между фактическими значениями результативного признака Коэффициент множественной корреляции служит критерием оценки точности функции регрессии. Чем его значение ближе к единице, тем сильнее факторные признаки влияют на результативный признак. Критериями оценки качества являются также отклонения Общая дисперсия (выборочная дисперсия) характеризует разброс наблюдаемых значений результативного признака
где Общую дисперсию можно разложить на две составляющие
где Остаточная дисперсия определяется по формуле:
где В качестве показателя интенсивности связи используют коэффициент детерминации – это отношение
показывающее часть полного рассеивания значений результативного признака под влиянием рассматриваемых факторных признаков. Чем больше коэффициент детерминации, тем лучше выбранная модель регрессии соответствует данным наблюдений. Если коэффициент детерминации равен единице, то все данные наблюдений расположены на линии регрессии. Важным критерием оценки качества полученной модели регрессии является оценка статистической значимости уравнения регрессии в целом и отдельных его параметров. Оценка статистической значимости уравнения регрессии в целом проводится с помощью Расчетное значение
где Критическое значение Если Оценить статистическую значимость параметров модели регрессии Расчетное значение
где Стандартные ошибки параметров модели регрессии – это их среднеквадратические отклонения, т.е. квадратные корни из дисперсий соответствующих параметров уравнения регрессии. Стандартные ошибки параметров модели парной линейной регрессии определяются по формулам: ¨ ¨ где Определяется критическое значение Примечание: Не учитывать статистическую значимость параметра При оценке качества модели регрессии возможны следующие случаи: ¨ Уравнение регрессии на основе проверки по ¨ Уравнение регрессии по критерию Фишера статистически значимо, но хотя бы один его параметр статистически незначим. В этом случае модель пригодна для принятия некоторых решений внутри выборки, но не для прогнозирования. ¨ Уравнение регрессии по критерию Фишера статистически незначимо. В этом случае модель регрессии считается ненадежной и непригодной для использования в практике.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.012 с.) |

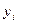 и соответствующими теоретическими значениями
и соответствующими теоретическими значениями  существует тесная зависимость, которую можно оценить с помощью коэффициента парной корреляции. Если значение коэффициента корреляции близко к единице, то качество модели высокое. Коэффициент парной корреляции определяется с помощью статистической функции КОРРЕЛ мастера функций. В диалоговом окне функции КОРРЕЛ в поле массив 1 вводится диапазон ячеек, занимаемых элементами массива результативного признака, а в поле массив 2 – диапазон ячеек, занимаемых расчетными значениями
существует тесная зависимость, которую можно оценить с помощью коэффициента парной корреляции. Если значение коэффициента корреляции близко к единице, то качество модели высокое. Коэффициент парной корреляции определяется с помощью статистической функции КОРРЕЛ мастера функций. В диалоговом окне функции КОРРЕЛ в поле массив 1 вводится диапазон ячеек, занимаемых элементами массива результативного признака, а в поле массив 2 – диапазон ячеек, занимаемых расчетными значениями 
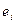 и их дисперсия. Чем больше отклонения (остатки), тем хуже модель регрессии и тем меньше коэффициент парной корреляции.
и их дисперсия. Чем больше отклонения (остатки), тем хуже модель регрессии и тем меньше коэффициент парной корреляции.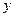 около его среднего значения и определяется по формуле
около его среднего значения и определяется по формуле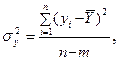 (17)
(17) – количество точек корреляционного поля,
– количество точек корреляционного поля, 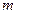 – число неизвестных параметров уравнения регрессии;
– число неизвестных параметров уравнения регрессии; 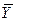 - среднее значение результативного признака.
- среднее значение результативного признака. (18)
(18) - дисперсия, вызванная регрессией
- дисперсия, вызванная регрессией  т.е. часть рассеивания значений результативного признака
т.е. часть рассеивания значений результативного признака 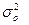 - остаточная дисперсия, т.е. часть рассеивания значений результативного признака, характеризуемая влиянием неучтенных факторных признаков. Чем меньше остаточная дисперсия, тем меньше влияние неучтенных факторных признаков и тем лучше математическая модель регрессии соответствует данным наблюдений, так как изменения результативного признака в этом случае в основном объясняется влиянием рассматриваемых факторных признаков.
- остаточная дисперсия, т.е. часть рассеивания значений результативного признака, характеризуемая влиянием неучтенных факторных признаков. Чем меньше остаточная дисперсия, тем меньше влияние неучтенных факторных признаков и тем лучше математическая модель регрессии соответствует данным наблюдений, так как изменения результативного признака в этом случае в основном объясняется влиянием рассматриваемых факторных признаков. (19)
(19)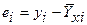 .
.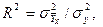 (20)
(20) – критерия Фишера, а оценка статистической значимости ее параметров проводится по
– критерия Фишера, а оценка статистической значимости ее параметров проводится по  – распределению Стьюдента.
– распределению Стьюдента. (21)
(21)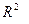 – коэффициент детерминации;
– коэффициент детерминации;  – объем выборки;
– объем выборки; 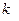 – количество факторных признаков линейной модели регрессии и количество параметров нелинейной модели регрессии, связанных с факторными признаками.
– количество факторных признаков линейной модели регрессии и количество параметров нелинейной модели регрессии, связанных с факторными признаками.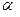 и числу степеней свободы:
и числу степеней свободы: 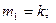
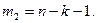 Обычно принимают
Обычно принимают 

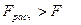 , то с вероятностью 1-a гипотеза о несоответствии заложенных в уравнение регрессии связей реально существующим отвергается и уравнение в целом статистически значимо, т.е. имеется хорошее соответствие данным наблюдений.
, то с вероятностью 1-a гипотеза о несоответствии заложенных в уравнение регрессии связей реально существующим отвергается и уравнение в целом статистически значимо, т.е. имеется хорошее соответствие данным наблюдений.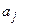 означает установить, существенно ли влияет факторный признак
означает установить, существенно ли влияет факторный признак 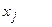 в генеральной совокупности на результативный признак
в генеральной совокупности на результативный признак  , т.е. может ли параметр модели регрессии принимать нулевое значение.
, т.е. может ли параметр модели регрессии принимать нулевое значение.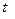 - статистики определяется по формуле:
- статистики определяется по формуле: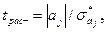 (22)
(22) – стандартное отклонение (стандартная ошибка) для параметра
– стандартное отклонение (стандартная ошибка) для параметра  статистики и стандартные ошибки выдаются в выходной информации инструмента «Регрессия».
статистики и стандартные ошибки выдаются в выходной информации инструмента «Регрессия».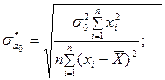 (23)
(23)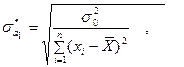 (24)
(24) - соответственно
- соответственно 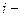 е и среднее значения факторного признака.
е и среднее значения факторного признака.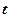 – статистики с помощью статистической функции СТЬЮДРАСПОБР мастера функций по уровню значимости
– статистики с помощью статистической функции СТЬЮДРАСПОБР мастера функций по уровню значимости 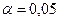 и числу степеней свободы
и числу степеней свободы  . Если
. Если  , то нулевую гипотезу о равенстве нулю параметра модели регрессии отвергают и параметр считают статистически значимым. Иначе, нет причин отвергать нулевую гипотезу.
, то нулевую гипотезу о равенстве нулю параметра модели регрессии отвергают и параметр считают статистически значимым. Иначе, нет причин отвергать нулевую гипотезу. при оценке качества линейной модели регрессии.
при оценке качества линейной модели регрессии.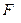 - критерию Фишера в целом статистически значимо и его параметры статистически значимы. Такая модель может быть использована для принятия решений и прогнозирования.
- критерию Фишера в целом статистически значимо и его параметры статистически значимы. Такая модель может быть использована для принятия решений и прогнозирования.


