
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Гаусса – Маркова для R-модели.Содержание книги Поиск на нашем сайте
Модель и основные этапы РА. РА предусматривает выполнение 3 этапов: 1 постулирование математической зависимости(регрессионной модели) 2 оценивание ее параметров 3 структурная идентификация оптимальной модели на основе статистического анализа. В общем случае регрессионная модель имеет вид: Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+Еi, i=1,n, где Y – отклик, x j– регрессоры, βо – параметры модели. Постулирование R – модели. 1 Постулируется R- модель в виде уравнения прямой Yi = β0 + β1*x1+Еi, i=1,n, где xi – неслучайная величина, Yi, Еi – случайные величины. 2.Мерой оптимальности подбора уравнения Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+Еi является мера S = ∑(yi – f(xi, β))2 3. Оценивание параметров R – модели. МНК. Способ оценивания параметров β0 и β1 зависит от принятой меры. Прямая линия должна быть такой, т е ее параметры β0 и β1 должны быть такими, чтобы сумма квадратов уклонений S была минимальной. Иначе говоря необходимо найти безусловный экстремум функции S=S(β) по аргументу β. Матричная запись. Исходя из уравнения Yi = β0 + β1*xi+Еi i=1,n можно записать матричное уравнение Y=Xβ+Е, где Y есть (n*1) вектор, x-(n*2) матрица, β – (2*1) вектор, Е – (N*1) вектор. Теорема Гаусса – Маркова для R-модели. В условии Yi = β0 + β1*xi+Еi, i=1,n или Y=Xβ+Е необходимо оценить не только два параметра модели β0 и β1 в виде b0 и b1 , но и числовую характеристику случайной величины Е, а именно, ее дисперсию δ2. Как случайная величина ошибки Е определяется математическим ожиданием М(Е) и дисперсией D(E)= δ2 Свойства оценки b0 и b1 (определены МНК). 1 Yi = β0 + β1*xi+Еi i=1,n 2. Xi – детерминированная величина. 3.1. М (εi) = 0; М (εi2) = D(εi) = δ2 3.2. M (εi εj)= 0 при I не равно о То оценки b0 и b1, полученные МНК, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок. Оценка точности для уравнения парной регрессии. Для уравнения регрессии необходимо кроме b0, b1 оценить D(εi) = δ2, а также дисперсии D(b0), D(b1) и D(Y^), Рассматривая ε, b0, b1 и Y^ как случайные величины. Оценку для δ2 вводят след образом.. Рассмотрим уравнение прогноза Y^ = b0+b1X для исходных точек (Yi,Xi), по которым получены МНК-оценки. Yi = β0 + β1*xi+Еi i=1,n, и остатки регрессии еi=yi-y^i, где xi – наблюдаемые значения отклика yi. Тогда yi можно записать в виде yi= b0+b1*xi +ei.
Остатки еi являются наблюдаемыми значениями случайных величин εi. Оценка δ2 в виде S2 = ^ δ2 связана с суммой квадратов остатков еi. Можно показать, что S2= δ2=∑ εi2/(n-2), а дисперсии b0, b1 и ковариация между ними запишутся в виде: D(b0)=S2b0=S2∑xi2/n∑(xi-Xср)2 D(b1)=S2b1=S2 ^cov(b0, b1 ) = - S2 где Xср = ∑xi/n. 6. Распределение МНК- оценок b0, b1 . Принятие предположения εi~N означает, что yi, имеют совместное нормальное распределение, т е для вектора Y справедлива запись Y ~Nn(Xβ,δ2In). Учитывая, что МНК-оценки b0, b1 являются линейными функциями от yi и, также имеют нормальное распределение b0 ~N (β0,δ2∑xi2/n∑(xi-Xср)2), b1 ~N(β0,δ2 Кроме того можно показать, что случайная величина(n-2)S2/ δ2 имеет распределение хи кадрат(n-2)? А дисперсия ошибок S2 не зависит от МНК – Оценок b0, b1 Интервальные оценки параметров R-модели. Если предполагать, что εi~N(0,δ2), То 100(1*λ/2)%ое доверительные интервалы для β0, β1 и y будут определяться след образом: в1 ± t(n-2,1-λ/2)* В0±t(n-2,1-λ/2)*S Y^n ±± t(n-2,1-λ/2)= S(1+1/n+ Таблица дисперсионного анализа и ее назначение в РА.
При использовании ДА оценивается влияние фактора На Y, т е степень адекватности регрессии выборочном наблюдениям. 9. Меры качества R и R2. Обычно генеральный коэффициент корреляции ρкоторый оценивается коэффициентом R, вводят с помощью формулы ρ2=(DY-σ2)/DY, где ρ=+√ρ2 называется коэффициентом множественной корреляции между Y и [x1….xp-1]. Выборочный коэф множеств. Корреляции между наблюденными величинами yi и вычисленными по модели величинами y^I: R= Критерии R и R2 (коэф детерминации) используют как меру линейной стохастической связи: чем больше значение R(0«R«1)? Тем сильнее связь, т е тем лучше f(X) соответствует наблюдениям. Мера R(R2 ) имеет дополнительное преимущество перед σ: имеет абсолютный характер при одной выборки наблюдений, поскольку оценивает степень тесности связи. Тем не менее и у этой меры есть свои недостатки: а) как и мера σ является внутренней мерой, т к построена по наблюдениям, по которым строится и модель, и мера; б) пригодна для проверки адекватности моделей относительно одной и той же выборки данных; в) используя эти меры, нельзя выявить набор значимых регрессоров; г) при увеличении количества регрессоров в модели значения R(R2) возрастают. Для устранения последнего недостатка соблюдают условие n>>p. Практически число наблюдений должно быть больше числа неизвестных в 5-15 раз. Кроме того вместо R(R2) предпочтительней применять так называемый скорректированный коэффициент множественной корреляции RC =√1-n(1-R2 )/(n-p) или скорректированный коэф множественной детерминации R2c.
Высокое значение R автоматически не гарантирует пригодность модели для прогноза и наоборот. F-критерий. Для оценки адекватности модели в целом и пригодности ее для прогноза можно использовать F-статистику F=MSR/S2. Ее использование превращает задачу сравнения двух дисперсий: дисперсии MSR, обусловленной регрессией, и остаточной дисперсии S2 . При этом необходимо установить, значимую ли часть полной дисперсии DY объясняет модель, содержащая в общем случае регрессоры X1….xp-1. Для этого выдвигается статистическая гипотеза H0 : β1=β2=….=β =0, т е гипотеза о том, что в модели Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+Еi. Вычисляя выборочное значение F-критерия и сравнивая его с табличным FT(λ, р-1, n-p), проверяют выполнение неравенства. При F<=FT гипотеза H0 (гипотеза о неадекватности модели) принимается, в противном случае регрессия признается значимой. На практике применяется правило: модель считается адекватной и пригодной для прогноза в случае, если F>4FT (λ, р-1, n-p). При известном R значение F-критерия можно определить по формуле F= Ошибка аппроксимации. Аср.= 1/n(∑(yi-yi^/yi))*100% 5%-7% - хорошее качество аппроксимации. Применение t-критерия. Tj=β^j/σ^j Статистика tj имеет для H0 t-распределение с n-p степенями свободы При значении |tj|>tтабл делается вывод об отличии от нуля коэффициента βj, следовательно о наличии влияния xj на Y При статистическом анализе регрессоров оценивается значимость каждого слагаемого модели, что дает возможность получить ее оптимальную структуру. Коэффициент эластичности. Э= y^э(производная) *x/y^ Постулирование MR-модели. Модель множественной регрессии (MR-модель) является обобщением линейной модели с зависимой и одной независимой переменными: Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+εi Матричная запись этой модель: Y=Xβ+ε, где Y есть (n*1) вектор (yi – случ. Величина) X- (n*p) матрица β – (p*1) вектор ε – (n*1) вектор Постулируется MR-модель в виде Y=Xβ+ε, где правая часть может быть представлена алгебраическими, тригонометрическими и другого вида полиномами, включая кусочно-полиномиальные и ортогональные полиномы, а так же разложение в ряд Тейлора, по сферическим функциям и др. Оцениваемые параметры βj в правые части Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+εi и Y=Xβ+ε входят линейно. Оценка точности MR-модели. Для MR-модели Оценку D(ε) =σ2 и D(β^)=D(b)=D(b0,b1….bp-1)Т) получаем следующим образом. Введем вектор предсказываемых значений отклика (вектор прогноза) Y^=xb и вектор остатков е=y-y^ тогда для MR-модели можно записать S2=σ^2=eTe/(n-p) Формула для D(b) получим формируя матрицу ковариаций для R-модели и обобщая ее D(b)=D(
Вынесем за скобки σ2, оставшееся выражение в скобках и есть (XTX)-1. Для MR-модели эту формулу можно получить путем прямых матричных действий. В силу симметричности матрицы (XTX)-1=((XTX)-1)Т имеем D(β^)=D((XTX)-1 *XTX)= (XTX)-1 *XT D(Y)((XTX)-1*XT)T =((XTX)-1 *XT D(Y)X(XTX)-1 Определим D(Y) где Y=xβ+ε в условиях гипотез D(ε) = σ2,In и детерминированность xβ, Как D(Y) = σ2,In Подставляя результат в предыдущую формулу получим D(β^)= D(b)= σ2(XTX)-1 X(XTX)-1 = σ2(XTX)-1 Определим дисперсию остатков. Для оценки дисперсии прогноза при заданном Xk, где XkT – вектор размера (1*р), можно использовать формулу D(Y^k)= S2 (1/n + XkT (XTX)-1Xk) Распределение МНК-оценки b. В условиях соблюдения предположения ε~Nn(0, σ2,In), как уже отмечалось, для Y справедлива запись Y~Nn(Xβ,σ2In)/ Для линейного регрессионного анализа у МНК-оценки вектора b=(b0,b1….bp-1)Т все элементы являются линейными комбинациями от yi. Одним из свойств многомерного нормального распределения является свойство: Линейная комбинация Гаусовского (нормального) вектора, есть гаусовская случайная величина, следоват. вектор b-есть случ. Вектор, имеющий многомерное нормальное распределение b~Nn(β,σ2(XTX)-1) Случайная величина (n-p) Дисперсия ошибок S2=σ2^= Внешние меры качества. Предполагалось, что в основном модели используются для прогноза – Вычислений Y^. Назовем такие модели моделями прогноза. Однако в ряде случаях исследователя интересуют только оцениваемые коэффициенты βj (j=0,р-1). Эти модели будем называть параметрическими. Для последних в качестве внутренних мер дополнительно можно использовать стандартные ошибки коэффициента σ^βj и недиагональные элементы матрицы ковариаций. Правда такой анализ имеет смысл делать только для конкурирующих структур одинаковой размерности. Под внешними мерами будем понимать меры, формируемые по данным не использованным при получении модели. а)Меры устойчивости βj.Эти меры используются как для модели прогноза, так и для параметрических моделей. При их формировании проверяется устойчивость β- коэффициентов модели, построенной по всем наблюдениям. Для этого полный ряд наблюдений делят на несколько серий, по каждой серии получают модели одного состава и размерности, как и для исследуемой модели, сравнивают β-коэф. Для моделей разных серий и этой модели, применяя соответствующие статистические критерии. При обнаружении значимых расхождений использование моделей или ее отдельных коэф-ов будет сомнительной.
в)меры качества прогноза. Внешние меры, характеризующие точность прогноза в случайном и систематическом отношении, основаны на разделение исходной выборки данных на 2 подвыборки: обучающую (модельную) и контрольную. При этом данные могут быть либо реально разделены на две части, либо контрольная часть будет искусственно сформирована на исходной полной выборке. Если выборка может быть разделена на две части, то обучающая подвыборка используется для построении модели. А контрольная дает возможность оценить качество прогноза по мерам, основанным на разностях Δi = (yi-y^i) для контрольных точек. При этом мера Δср.= ∑Δi/k или ее абсолютное значение будет оценкой систематического смещения, а мера σΔ=√∑(Δi-Δср.)2/(k-p) – оценкой случайной ошибки. Вопрос 29. Предположение о векторе β. По оцениваемому параметру β принимаются гипотезы:< 2.1>-адекватная наблюдениям модель (2.1)- Y=Xβ+ε линейна по элементам вектора β;<2.2>на вектор β не наложено ограничений, т.е. о векторе β нам априори ничего не известно;<2.3>- элементы β вычислены с пренебрежимо малой компьютерной ошибкой.
В.30 Предположение о матрице X. <3.1>- регрессоры x0,x1,….,xp-1 являются линейно-независимыми векторами матрицы X или справедлива запись rankX=p; <3.2> - элементы матрицы Xне являются случайными величинами. В.31 Предположения о векторе ε. Предположения о векторе ошибок ε. <4.1>- ошибки εi являются случайными ошибками, аддитивно входящими в модель (2.1)- Y=Xβ+ε. Вообще можно предполагать ошибки, входящие в модель мультипликативно, например, yi=(β0+∑(p-1j=1)βjxij)(1+εi). В этом случае характер остальных предположений на вектор ε изменится. <4.2>-ошибки εiраспределены по нормальному закону. Если это так, то МНК-оценки в условиях теоремы Гаусса-Маркова дополнительно обладают свойством эффективности для всех классов несмещённых оценок (а не только в классе линейных оценок). Кроме этого возможно применение статистик для интервального оценивания, проверки соблюдения ряда гипотез и качества модели, а также заключения о статистической независимости. <4.3>- ошибки εiне содержит систематического смещения. При такой гипотезе систематические ошибки, ВЫЗВАННЫЕ НЕУЧТЁННЫМИ ЭФФЕКТАМИ, ВОЙДУТ В β0. <4.4>- ошибки εiимеют постоянную дисперсию,т.е. наблюдения Y1,….,ynне коррелированы и при справедливости <4.2> статистически независимы. В.32. Предположение о матрице X. <3.1>- регрессоры x0,x1,….,xp-1 являются линейно-независимыми векторами матрицы X или справедлива запись rankX=p; <3.2> - элементы матрицы Xне являются случайными величинами. гипотезы:< 2.1>-адекватная наблюдениям модель (2.1)- Y=Xβ+ε линейна по элементам вектора β;<2.2>на вектор β не наложено ограничений, т.е. о векторе β нам априори ничего не известно;<2.3>- элементы β вычислены с пренебрежимо малой компьютерной ошибкой.) Дополнительно введём следующие два предположения. <5/1>- метод поиска оптимального набора регрессоров {xj:j=1,p1;p1<p} для Yявляется точным. Очевидно, при однокритериальном поиске оптимальной модели из 2p-1 возможным является метод полного перебора. До сих пор рассматривалась MR-модель для одного отклика называемая многооткликовая регрессия, для которой будем считать регрессионные модели независимыми друг от друга.Итак, <5.1>- для многооткликовой задачи правомерно применение МНК к каждой из регрессии в отдельности.
В.34. В. 33. Методология РМ. На начальном этапе адаптивный РМ-подход предусматривает применение линейной по оцениваемым параметрам модели и вычисленной схеме МНК; на последующих этапах:- проверку соблюдения гипотез РА-МНК, ранжирование нарушений по степени искажения свойств НЛО-оценок β˄ или Y˄ в зависимости от назначения модели (прогноз, описание или описание и прогноз);- последовательную адаптацию к нарушениям путём применения соответствующих вычислительных процедур; - проверки нарушений и ранжирование при необходимости. Основными элементами РМ-подхода, формирующими НЛО параметров и прогноза, являются выработка, функции, методы оценивания и структурной идентификации, а также вычислительные сценарии адаптации. В.35. В.36. Анализ соблюдения предположений по вектору β и процедуры адаптации. Нарушение <2.1>. Рассмотрим случай, когда линейная модель yi=β0+β1*xi,1+…+βp-1*xi,p-1+εi, i=1,n͞ признаётся в целом адекватной и пригодной для описания или прогноза, однако она может быть улучшена по структуре путём устранения избыточных регрессоров или введением значимых факторов. Такими признаками нарушения,<2.1>являются:- при избыточности наличие слагаемых в модели со значениями t≤tт или p-level≥α, где α-принятый уровень значимости (обычно α=0,05), tт- критическое значение t- статистики при соответствующем α; -при недоопределённости тренды на графиках остатков (dY˄;xj), отличающиеся от горизонтальной равномерной полосы шириной +/- 2*Ϭ. Если модель избыточна, то логично устранить незначимую переменную и пересчитать заново β-коэффициенты. При одновременном нарушении предположений <2.1>и <3.1>простой вывод незначимых переменных переменныхxj–рискованная процедура. В этом случае применяют метод пошаговой регрессии или другие способы. При неопределённости модели следует искать пропущенные факторы (xk,xj2,t,…).Если модель сразу признаётся неадекватной, то необходимо перейти к другому классу линейных базовых функций или применить модель, нелинейную по β, и нелинейный МНК. Нарушение <2.2>. Это условие может быть нарушено для параметрических (описательных) моделей. Специальных признаков нарушения не существует. Косвенными признаками могут быть и признаки нарушения <3.1>, а именно, значимые коэффициенты парной корреляции. Адаптация путём учёта ограниченной на вектор β приводит к решению задачи на поиск экстремума функции с линейными или нелинейными ограничениями. Нарушение<2.3>. О необходимости устранения β0 судят, исходя их существа процесса или из результатов сравнения по внешним критериям качествам. Если модель yi=β0+β1*xi,1+…+βp-1*xi,p-1+εi, i=1,n͞ не содержит аддитивную постоянную β0, то не всякая регрессионная процедура из пакета прикладных программ (ППП) может быть применена для вычислительной обработки. Современные ППП обычно предусматривают два режима расчётов: с β0 и без β0. В. 37. В.38. Анализ соблюдения предположений по вектору ε и процедуры адаптации. Нарушение <4.1>. Обычно нарушение об аддитивности ε происходит при переходе от нелинейной по β модели (внутренне линейной) К ЛИНЕЙНОЙ И КОСВЕННО ОБНАРУЖИВАЕТСЯ ПО ЯВЛЕНИЮ ГЕТЕРОСКЕДАСТИЧНОСТИ НА ГРАФИКЕ (d,Y˄) для преобразованной модели. Гетероскедастичностью называется явление увеличения или уменьшения дисперсии от Y˄ или xj.Для получения ошибок, удовлетворяющих условиям теоремы Гаусса-Маркова, можно преобразовать Y и при необходимости xj(j=0,p-1). В общем случае это достаточно трудно. Нарушение <4.2>. Для проверки нарушения условия ε~Nnприменяются как графические, так и аналитические способы. В первом случае можно использовать нормальную вероятную бумагу или её аналоги; график (d,Y˄) в виде тренда шириной +/- 2Ϭ, равномерно заполненный на 95%, помимо адекватности модели свидетельствует о нормальности e. Кроме того предположение о нормальности нарушается, если наблюдения обременены аномальными выбросами. Если на графиках остатков (d,Y˄;xj) за пределами полосы +/- 3Ϭ присутствуют точки, то условие <4.2> следует считать нарушенным. Из аналитических критериев распространены критерий «хи квадрат», Колмогорова – Смирнова (n≥100), а также критерий Шапиро и Уилка (n≥20). Нормальность приблизительно может быть оценена по методу Айвазяна. Адаптация к нарушению <4.2>может быть выполнена удалением выбросов, а также дополнительно применением робастных (устойчивых) методов оценивая. Нарушение <4.3>. Условие M(εi)=0 не требует особого внимания при наличии β0 в модели. Отличие оiт нуля d͞=∑(n,i=1) (ei/S) обычно сигнализирует об ошибках в расчётах. Нарушение <4.4>. Нарушение условия постоянства дисперсии Ϭ͞2 обычно проверяется по графикам остатков (d,Y˄,xj). Выбор схемы адаптации к нарушению <4.3> зависит от возможности описать неоднородность дисперсии аналитическим соотношениям или от возможности оценить дисперсии наблюдений (или веса). Если, например, можно определить матрицу ковариаций D(Y˄) после первого приближения МНК, то применяют схему взвешанного МНК. Нарушение <4.5>. Для проверки условия независимости ошибок из-за неучета фактора времени используют графики остатков (d,T), где T-время или номер наблюдения. По виду кривых делается вывод о необходимости введения линейного или нелинейного слагаемого по T. Для выявления взаимных корреляций между ei(авторегрессий первого порядка) используют критерий Дарбина- Уотсона (Dили DW-критерий). В этом случае анализируются зависимости вида εi=ρεi-1+ε`I, где ε`I~N(0,Ϭ2). Адаптация к нарушению <4.5>из-за пропуска Tвыполняется введением Т (или Т2). Если и после этого остаётся авторегрессия, фиксируемая по D– критерию, то прибегают к обобщённому МНК, используя оценку параметра авторегрессии ρ. В.39. В.40. Обобщённый МНК. Рассмотрим вначале более общий случай, когда для модели Y=Xβ+εвыполняются все условия за исключением двух (<4.4>,<4.5>): D(ε)=Ω, причём Ω-недиагональная матрица ковариаций. Если применить обычный МНК, то β˄ останется несмещённой оценкой, однако оценка матрицы ковариаций вектора β˄, т.е. D(β˄), окажется смещённой, что приведёт к неэффективности оценок β˄. Формально для получения наилучших линейных оценок необходимо воспользоваться обобщённым МНК (ОМНК), теоретическим основанием которого является теорема: Теорема Айткена: В классе линейных несмещённых оценок вектора β для обобщённой регрессионной модели оценка β0˄=(XTΩ-1X-1) -1XTΩ-1Yимеет наименьшую матрицу ковариаций. Последняя в этом случае запишется в виде D(β˄0)=(XTΩ-1X) -1. Следует отметить, что при D(ε)=Ωмера R2не может быть использована для оценки качества модели. Для применения ОМНК необходимо знать матрицу Ω, которая на практике обычно не известна. Так как в общем случае Ω содержит n(n+1)/2 неизвестных элементов, то по nнаблюдениям невозможно получить из наилучшие линейные оценки. Приближением к ОМНК является так называемый «доступный» ОМНК, в котором на структуру Ω вводят дополнительные условия. В.41. Взвешенный МНК. Применим ОМНК для случая, когда матрица ковариаций Ω вектора ошибок ε диагональна, иначе говоря, D(εi)=Ϭ2i (i=1,n). Часто используют представление Ϭ2i=Ϭ2wi, где числа wi нормированы так, что ∑wi=n.При wi=1 (i=1,n) получаем обычный классический случай. Алгоритм ОМНК здесь достаточно прост, так как он сводится к применению обычного МНК к избыточной системе уравнений Yi/Ϭi=∑(p-1,j=0) βj*(xij/Ϭi+ εi/Ϭi); (i=1,n), где M(εi/Ϭi)=0, cov(εi/Ϭi, εj/Ϭj)=0 при i не равен j. Применение ВМНК приводит к уменьшению стандартных ошибок оценок βj˄ по сравнению с обычным МНК. В.42. Модель и основные этапы РА. РА предусматривает выполнение 3 этапов: 1 постулирование математической зависимости(регрессионной модели) 2 оценивание ее параметров 3 структурная идентификация оптимальной модели на основе статистического анализа. В общем случае регрессионная модель имеет вид: Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+Еi, i=1,n, где Y – отклик, x j– регрессоры, βо – параметры модели. Постулирование R – модели. 1 Постулируется R- модель в виде уравнения прямой Yi = β0 + β1*x1+Еi, i=1,n, где xi – неслучайная величина, Yi, Еi – случайные величины. 2.Мерой оптимальности подбора уравнения Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+Еi является мера S = ∑(yi – f(xi, β))2 3. Оценивание параметров R – модели. МНК. Способ оценивания параметров β0 и β1 зависит от принятой меры. Прямая линия должна быть такой, т е ее параметры β0 и β1 должны быть такими, чтобы сумма квадратов уклонений S была минимальной. Иначе говоря необходимо найти безусловный экстремум функции S=S(β) по аргументу β. Матричная запись. Исходя из уравнения Yi = β0 + β1*xi+Еi i=1,n можно записать матричное уравнение Y=Xβ+Е, где Y есть (n*1) вектор, x-(n*2) матрица, β – (2*1) вектор, Е – (N*1) вектор. Теорема Гаусса – Маркова для R-модели. В условии Yi = β0 + β1*xi+Еi, i=1,n или Y=Xβ+Е необходимо оценить не только два параметра модели β0 и β1 в виде b0 и b1 , но и числовую характеристику случайной величины Е, а именно, ее дисперсию δ2. Как случайная величина ошибки Е определяется математическим ожиданием М(Е) и дисперсией D(E)= δ2 Свойства оценки b0 и b1 (определены МНК). 1 Yi = β0 + β1*xi+Еi i=1,n 2. Xi – детерминированная величина. 3.1. М (εi) = 0; М (εi2) = D(εi) = δ2 3.2. M (εi εj)= 0 при I не равно о То оценки b0 и b1, полученные МНК, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 879; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.113.0 (0.015 с.) |



 .
.

 )1/2 где t(n-2,1-λ/2) это (1-λ/2)% ая точка T-распределение с (n-2) степенями свободами обычно λ=0,05.
)1/2 где t(n-2,1-λ/2) это (1-λ/2)% ая точка T-распределение с (n-2) степенями свободами обычно λ=0,05. или пользуясь таблицей ДА по формуле R=+√SSR/SS.
или пользуясь таблицей ДА по формуле R=+√SSR/SS. или для линейной парной регрессии F=(n-2)
или для линейной парной регрессии F=(n-2) 
 )= (
)= ( )=(
)=( )
)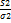 ~ X2(хи)(n-p)
~ X2(хи)(n-p)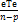 =
=  не зависит от вектора MNK-оценки b=β^
не зависит от вектора MNK-оценки b=β^


