
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение частного F-критерия.Содержание книги Поиск на нашем сайте
Оценив качество регрессии в целом, можно ее улучшить, анализируя каждый регрессор в отдельности. Признав регрессию значимой по общему F-критерию, т е отклонив гипотезу H0 : β1=β2=….=β =0 или H0:p=0, Можно приступить к проверке гипотез H0 : βj=0(j=1,р-1). Это даст возможность в принципе получить модель меньшей размерности. Наиболее просто гипотеза проверяется по частному F-критерию Fj=βj2^/σ^2j, где σ^2j являются диагональными элементами матрицы ковариаций D(β^)=D(b)/ При справедливости гипотезы H0 эта статистика имеет F-распределение с 1 и (n-p) степенями свободы. При Fj<=FT гипотеза H0:βj=0 принимается, в противном случае регрессор Xj признается значимым. Применение t-критерия. Tj=β^j/σ^j Статистика tj имеет для H0 t-распределение с n-p степенями свободы При значении |tj|>tтабл делается вывод об отличии от нуля коэффициента βj, следовательно о наличии влияния xj на Y При статистическом анализе регрессоров оценивается значимость каждого слагаемого модели, что дает возможность получить ее оптимальную структуру. Коэффициент эластичности. Э= y^э(производная) *x/y^ Постулирование MR-модели. Модель множественной регрессии (MR-модель) является обобщением линейной модели с зависимой и одной независимой переменными: Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+εi Матричная запись этой модель: Y=Xβ+ε, где Y есть (n*1) вектор (yi – случ. Величина) X- (n*p) матрица β – (p*1) вектор ε – (n*1) вектор Постулируется MR-модель в виде Y=Xβ+ε, где правая часть может быть представлена алгебраическими, тригонометрическими и другого вида полиномами, включая кусочно-полиномиальные и ортогональные полиномы, а так же разложение в ряд Тейлора, по сферическим функциям и др. Оцениваемые параметры βj в правые части Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+εi и Y=Xβ+ε входят линейно. Оценивание параметров MR-модели. Основные предположения. Обобщим предположения РА-МНК для парной регрессии на случай MR-модели. 1. Yi = β0 + β1*x1,i+…+βp-1*xi,p-1+εi Y=Xβ+ε 2. Xi,1….Xi,p-1 – детерминированные величины. Векторы Xi,1….Xi,p-1 – линейно независимы в пространстве Rn 3. 3.1 M(εi)=0 M(εi2)=D(εi)=σ2 или в матричном виде M(ε)=0, D(ε)=M(εTε)=σ2In. 3.2 Ошибки εi для разных наблюдений не коррелированны, т е (εiεj)=cov(εiεj)=βij=σiσj=0 при i≠j 3.3 εi ~ N(0,σ2) i=1,n ε~Nn(0, σ2,In) MNK. В многомерном случае применение MNK для оценивания вектора β озночает решение задачи на поиск экстремума (минимума) функции S=S(β), где S=∑εi2=εTε Дифференцируя εTε по вектору β и приравниваем результат к нулю, получаем нормальное уравнение вида XTXβ=XTY, где β=(β0β1….βр-1)T Решение этой системы есть MNK – оценка b=(b0,b1….bp-1)Т параметров вектора β b=b^=(XTX)-1XTY Теорема Гаусса-Маркова для MR-модели. Если будут выполняться предположения 1 Y=Xβ+ε 2 X-детерминированная (n *p) матрица, имеющая максимальный ранг p 3.M(ε)=0, D(ε)=M(εTε)= σ2,In, то MNK – оценка β^=M(XTX)-1 XTY, является наиболее эффективной оценкой в классе линейных несмещенных оценок. Оценка точности MR-модели. Для MR-модели Оценку D(ε) =σ2 и D(β^)=D(b)=D(b0,b1….bp-1)Т) получаем следующим образом. Введем вектор предсказываемых значений отклика (вектор прогноза) Y^=xb и вектор остатков е=y-y^ тогда для MR-модели можно записать S2=σ^2=eTe/(n-p) Формула для D(b) получим формируя матрицу ковариаций для R-модели и обобщая ее D(b)=D( Вынесем за скобки σ2, оставшееся выражение в скобках и есть (XTX)-1. Для MR-модели эту формулу можно получить путем прямых матричных действий. В силу симметричности матрицы (XTX)-1=((XTX)-1)Т имеем D(β^)=D((XTX)-1 *XTX)= (XTX)-1 *XT D(Y)((XTX)-1*XT)T =((XTX)-1 *XT D(Y)X(XTX)-1 Определим D(Y) где Y=xβ+ε в условиях гипотез D(ε) = σ2,In и детерминированность xβ, Как D(Y) = σ2,In Подставляя результат в предыдущую формулу получим D(β^)= D(b)= σ2(XTX)-1 X(XTX)-1 = σ2(XTX)-1 Определим дисперсию остатков. Для оценки дисперсии прогноза при заданном Xk, где XkT – вектор размера (1*р), можно использовать формулу D(Y^k)= S2 (1/n + XkT (XTX)-1Xk) Распределение МНК-оценки b. В условиях соблюдения предположения ε~Nn(0, σ2,In), как уже отмечалось, для Y справедлива запись Y~Nn(Xβ,σ2In)/ Для линейного регрессионного анализа у МНК-оценки вектора b=(b0,b1….bp-1)Т все элементы являются линейными комбинациями от yi. Одним из свойств многомерного нормального распределения является свойство: Линейная комбинация Гаусовского (нормального) вектора, есть гаусовская случайная величина, следоват. вектор b-есть случ. Вектор, имеющий многомерное нормальное распределение b~Nn(β,σ2(XTX)-1) Случайная величина (n-p) Дисперсия ошибок S2=σ2^=
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.009 с.) |

 )= (
)= ( )=(
)=( )
)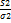 ~ X2(хи)(n-p)
~ X2(хи)(n-p)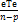 =
=  не зависит от вектора MNK-оценки b=β^
не зависит от вектора MNK-оценки b=β^


