
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частный случай применения доступного ОМНК.Содержание книги Поиск на нашем сайте
Как правило, ошибки Ϭi (i=1,n) неизвестны. Для их оценки используем частное условие: стандартное отклонение ошибки пропорционально независимой переменной. Иногда априори можно считать, что Ϭi прямо пропорционально одной из переменных xi, т.е. Ϭi2=Ϭi2 xij2.Чтобы перейти к классическому случаю разделим каждое уравнение системы Yi=∑(p-1,j=0) βj*xij+ εi; (i=1,n)на xilи введём новые регрессоры xij`=xij/xilи отклики y`i=yi/xil (i=1,n; j=1,p-1). При таком преобразовании МНК-оценки β˄jне изменится. Следует только иметь в виду, что если xi0=1, то МНК-оценки свободного члена и коэффициента при x`il=1/xilв новой модели будут оценками соответственно коэффициенты при xil и свободного члена в старой модели. 43. Адаптация к корреляции по времени. Ошибки εi в моделях, построенных по выполненным в разное время наблюдениям, часто коррелируют друг с другом. Запишем MR-модель, заменяя индекс i на t, в виде yt=β0+β1xt1+...+βp-1xt,p-1+εt, где t-момент времени (t=1,n). Самое простое предположение о виде зависимости между εt состоит в том, что случайная последовательность {εt;t=1,n} образует авторегрессионный процесс первого порядка εt=ρ· εt-1 +ut, где {ut;t=1,n}-последовательность независимых нормально распределенных случайных величин с нулевым средним и постоянной дисперсией σu2; ρ-коэффициент корреляции между двумя соседними ошибками, а cov(εt, εt-m)=ρm σε2, где σε2= σu2/(1-ρ2) для всех εt (t=1,n). Тогда матрица ковариации для ε запишется в виде Ω= σu2/(1-ρ2) Рассмотрим теперь, как оценить параметры модели при неизвестном заранее ρ. Наиболее популярным считается алгоритм Кохрейна-Оркатта, содержащий этапы: 1) система решается обычным МНК; фиксируется вектор остатков 2) МНК-оценка в регрессии принимается за приближенное значение ρ 3) выполняется преобразование yt-ρyt-1=β0(1-ρ)+β1(yt,1-ρyt-1,1)+...+βp-1(yt,p-1-ρyt-1,p-1)+ut при ρ=z и определяется МНК-оценка Рассмотрим несколько подробнее критерий Дарбина-Уотсона (DW), введенный ранее для обнаружения корреляции во времени первого порядка. Значение DW можно оценить по формуле DW=2(1-r). По не видно, что если между et и et-1 есть высокая положительная корреляция, то DW->0; отсутствие корреляции (r->0) означает, что DW->2. При высокой отрицательной корреляции DW->4. 44. Введение качественных (фиктивных) переменных. Предположим, что нарушается последнее предположение, т. е. пропущены один или несколько значимых переменных-регрессоров. Однако эти переменные имеют качественный характер, принимая два или более дискретных значения. Например, при изучении зависимости зарплаты работника от ряда факторов естественно ввести переменную xk «высшее образование», где xk может принимать значение «0» или «1». При сдельной оплате труда можно ввести переменную «квартал», принимающую четыре значения и т. д. Такие переменные получили название – «фиктивные» переменные. Рассмотрим, как эти переменные ввести в MR-модель. Пусть в модель вводится пропущенный фактор xk, отражающий тот факт, что два типа образования (0,1) дают различные значения отклика y в дополнение к тем изменениям, которые порождены другими факторами. Решение задачи возможно двумя способами. Первый состоит в том, чтобы включить в модель yt=β0+β1xt1+...+βp-1xt,p-1+εt, t=1,n фиктивную переменную z и коэффициент регрессии α yi= Коэффициент α можно оценить одновременно с β-коэффициентами. Фактору z можно приписать следующие значения: z=0, если работник не имеет высшего образования (ВО), и z=1 – в противном случае. Иногда удобнее другие обозначения. Пусть имеется n наблюдений (работников). Из них n1 не имеет высшего образования, а n2=n-n1- имеет. Если применять формулы для вычисления значений z z=-n2/√ n1n2(n1+ n2) при отсутствии ВО, z=n2/√ n1n2(n1+ n2) при наличии ВО, то соответствующий столбец матрицы x будет ортогональным к столбцу «β0». Принимая модель, мы считаем, что средняя зарплата есть Если качественный признак z имеет число значений, большее двух, то обычно вместо придания переменной z нескольких значений переходят к двум и более фиктивным переменным, принимающим бинарный значения. Если нужно рассматривать три различных уровня образования, то необходимы две фиктивные переменные z1 и z2. Тогда получим (z1, z2)=(1,0) без ВО, (z1, z2)=(0,1) с ВО, (z1, z2)=(0,0) со средним техническим образованием и модель будет включать дополнительные слагаемые (α1z1+α2z2) с оцениваемыми коэффициентами α1 и α2. 45. Переход к нелинейной по β модели. До сих пор мы конструировали модели, линейные относительно параметров βj y=β0+β1z1+...+βpzp+ε, где zj (j=1,p) в общем случае функции от основных независимых переменных x1,...,xk. Есть много ситуаций, в которых модель вида y=β0+β1z1+...+βpzp+ε не пригодна для описания. Любую модель, не имеющую вида y=β0+β1z1+...+βpzp+ε, будем называть нелинейной моделью, т. е. моделью, нелинейной относительно параметров βj. Пример уравнения: y=exp(β1+β2t2 +ε)где β1, β2 – нелинейно входящие в модель оцениваемые параметры, случайная ошибка ε~N(0,σ2). Модель y=exp(β1+β2t2 +ε) путем логарифмирования по основанию e может быть приведена к форме lny=β1+β2t2 +ε, имеющая вид βj y=β0+β1z1+...+βpzp+ε и линейной относительно параметров. В этом случае говорят, что модель y=exp(β1+β2t2 +ε) является внутренне линейной. 46. Система линейных одновременных уравнений. Основные понятия. Пусть на основании предположений экономиста-теоретика сформулирована следующая макроэкономическая модель в виде трех соотношений: y1t=α0+α1(y3t -x1t)+ε1t, y2t= β1y3,t-1+β2x2t +ε2t, y3t= y1t+y2t +x3t; t=1,n, где y1 – потребление, y2 – инвестиции, y3 – национальный доход; x1 – подоходный налог, x2 – норма процента как инструмент гос. регулирования, x3 – гос. закупки товаров и услуг для каждого момента времени t. Медоль y1t=α0+α1(y3t -x1t)+ε1t, y2t= β1y3,t-1+β2x2t +ε2t, y3t= y1t+y2t +x3t содержит два уравнения, объясняющие поведение потребителей и инвесторов, и одно тождество; причем в y2t= β1y3,t-1+β2x2t +ε2t используется запаздывание (лаг) в один период для отражения воздействия нац. дохода на инвестиции. Используемые в модели переменные подразделяются на эндогенные, экзогенные и предопределенные. Эндогенными называются переменные, внутренние по отношению к рассматриваемой экономической (ли другой) системе. Они – взаимозависимы и являются основным объектом рассмотрения. Экзогенные переменные – это переменные, задаваемые (планируемые для экономических задач) извне. Предполагается, что они независимы друг от друга и от ошибок ε. Предопределенными переменными обычно называют аргументы или объясняющие переменные в правых частях, включая лаговые эндогенные переменные. В нашей модели y1, y2, y3 – экзогенные, а x1, x2, x3 – и лаговая эндогенная переменная y3,t-1 – предопределенные переменные. Так что назначение модели y1t=α0+α1(y3t -x1t)+ε1t, y2t= β1y3,t-1+β2x2t +ε2t, y3t= y1t+y2t +x3t – объяснение поведения эндогенных переменных в зависимости от экзогенных и лаговых эндогенных переменных. 47. Проблема идентификации модели. Структурный коэффициент идентифицируем, если он может быть вычислен через коэффициент приведенной формы (соответственно уравнение системы будет называться идентифицируемым, если все его коэффициенты идентифицируемы). Обозначим число эндогенных переменных через j, а число экзогенных переменных через D. Модель идентифицируема, если все структурные коэффициенты определены однозначно единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. Необходимое условие идентифицируемости: если D+1=Н, то уравнение идентифицируемо; если D+1<H, то уравнение неидентифицируемо; если D +1>Н, то уравнение сверхидентифицируемо. Достаточное уравнение идентифицируемости: уравнение идентифицируемо, если по отсутствующим в нем переменным можно из коэффициентах при них в других уравнениях системы получить матрицу, определитель которой не равен 0, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. 48. Косвенный МНК. Одной из вычислительных схем решения отдельных уравнений СОУ является косвенный МНК (КМНК). Пусть решается первое уравнение структурной формы модели, содержащее k1 эндогенных и p1 экзогенных переменных, и пусть соблюдаются все шесть заявленных условий (в том числе условие идентифицируемости). Коэффициент при y1 равен 1. Алгоритм КМНК включает в себя: 1) оценивание МНК коэффициентов приведенной формы; 2) решение систем β+Т·C+,-=-α+Т, β+Т·C+,--=Op-p1 путем замены элементов матрицы C их МНК-оценками. Область применения КМНК довольно ограничена, т. к. чаще всего условие (p-p1)≥(k1-1) выполняется со знаком «>», т. е. число уравнений превышает число неизвестных. В этом случае возникают проблемы как выбора вариантов оценок, так и трудности алгоритмизации. Для решения применяют двухшаговый МНК. 49. Двухшаговый МНК. Алгоритм 2ШМНК предусматривает следующие этапы: 1) оцениваются коэффициенты приведенной формы обычным МНК y1=xC1+M, где C1(p×(k1-1)) – матрица приведенных коэффициентов, M(n×(k1-1)) – матрица ошибок. Здесь каждый столбец матрицы Y1 рассматривается совместно с одним и тем же набором столбцов X; 2) вычисляется прогноз Ŷ1=XĈ1; 3) вычисляются оценки структурных коэффициентов β1 и α1 в модели y1=Y1β1+X1α1+ε1 после замены Y1 на Ŷ1. Если условие (p-p1)≥(k1-1) выполняется со знаком «=» и справедливо условие rank C+,--= k1-1, то 2ШМНК-оценка совпадает с оценкой КМНК. 50. Трезшаговый МНК. 3НМНК можно применить в том случае, когда остатки в различных структурных уравнениях Byt+Axt=εt коррелируют друг с другом, т. е. их матрица ковариаций не является диагональной. По сути, применение 3НМНК обозначает применение ОМНК к результатам 2НМНК. В соответствии с этим отметим только основные этапы алгоритма: 1) оценивают коэффициенты СОУ с помощью 2ШМНК; 2) вычисляют остатки для каждого структурного уравнения; 3) получают матрицу ковариации остатков; 4) оценивают коэффициенты СОУ обобщенным МНК. Естественно, 3НМНК применяют при тех же условиях 1-6, при которых применяется 2ШМНК. Есть матрица ковариации ∑ для структурных остатков может быть приведена к блочно-диагональному виду, то процедуру 3НМНК удобнее применять отдельно для каждого блока.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.237 (0.011 с.) |


 4) фиксируется новый вектор e=y-x
4) фиксируется новый вектор e=y-x 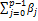 xij+αzi+εt; i=1,n.
xij+αzi+εt; i=1,n.


