
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Прикладная математика»Содержание книги Поиск на нашем сайте
Кафедра «Прикладная математика»
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ ДАННЫХ НАБЛЮДЕНИЙ Методические указания и задания Днепропетровск – 2008
Кореляційно-регресійний аналіз даних спостережень. Методичнi вказiвки та завдання для аспiрантiв, магiстрiв та студентiв усiх форм навчання академії/ Укладач: Єршова Н.М. – Днiпропетровськ: ПДАБА, 2008. - 59 с. – рос. мовою. Укладач: Єршова Н.М.
Вiдповiдальний за випуск: Н.М. Єршова, д.т.н., проф., зав. кафедрою прикладної математики ПДАБА
Рецензент: Л.В. Цибрiй, к.ф.-м.н., доц. ПДАБА
Затверджено на засiданнi кафедри прикладної математики протокол №1 від 2.09.2008 р.
Затверджено на засiданнi методичної ради ПДАБА протокол № 1(54) від 30.10.2008 р.
СОДЕРЖАНИЕ Введение 4 Задание 5 Методические вопросы работы 9 Выбор варианта задания………………………………………9 Содержание пояснительной записки………………………..10 Оформление пояснительной записки……………………….10 Защита работы………………………………………………...12 Содержание и последовательность выполнения работы 12 1. Краткие сведения из теории и компьютерной технологии 14 1.1. Контроль исходной информации на наличие грубых ошибок и выбросов 15 1.2. Проверка соответствия исследуемых признаков нормальному закону распределения ………………16 1.3. Корреляционный анализ статистических данных………19 1.4.Регрессионный анализ статистических данных 24 1.4.1. Парный линейный регрессионный анализ 26 1.4.2. Парный нелинейный регрессионный анализ 27 1.4.3. Многомерный линейный регрессионный анализ 28 1.4.4. Многомерный нелинейный регрессионный анализ 29 1.5. Критерии оценки качества модели регрессии 29 1.6. Прогнозирование на основе уравнения регрессии 33 1.7. Экономический смысл параметров модели регрессии 34 1.8. Прогнозирование на основе методов оптимизации…….34 2 Пример выполнения задания 35 Список литературы 58 Приложение 1. Образец оформления титульного листа 59
Введение
Построение и исследование на компьютере модели экономического явления не является самоцелью: это лишь средство для проведения наиболее важного и ответственного этапа – принятия управленческого решения, наилучшего в рассматриваемой ситуации. Выбор решения может осуществляться в условиях определенности, неопределенности и риска. Риск в задачах исследования операций – мера несоответствия между разными возможными результатами решения. Задачи с риском – это задачи, возникающие в ситуациях, когда считается, что каждая выбираемая стратегия может привести к разным результатам и вероятности тех или иных результатов принимаемого решения известны или могут быть оценены. Выбор решения в условиях определенности сводится к следующему: имеется множество допустимых решений, требуется из этого множества выбрать такое решение, которое обеспечит экстремум (минимум или максимум) целевой функции. Это детерминированные задачи, например, математического программирования, в которых каждая стратегия дает единственный результат. Принятие решений в условиях неопределенности отличаются тем, что результаты стратегии непредсказуемы. Учебной и рабочей программами дисциплины «Экономико-математическое моделирование» предусмотрено выполнение корреляционно-регрессионного анализа данных наблюдений. Эта задача относится к задачам выбора решений в условиях неопределенности, т.е. результаты выбора непредсказуемы. При ее решении студент использует знания по дисциплинам «Высшая математика», «Экономическая информатика», «Теория вероятностей и математическая статистика» и развивает навыки моделирования на компьютере. Цель работы: ¨ Изучить методику проведения корреляционно-регрессионного анализа статистических данных. ¨ Освоить методику решения экономических задач в среде приложения Excel (мастер функций, надстройка «Поиск решения» и инструменты пакета анализа). ¨ Привить навыки оформления в среде текстового редактора Word пояснительной записки, содержащей таблицы, графики и формулы. ¨ Развить навыки защиты выполненной работы. ЗАДАНИЕ В таблице 1 приведены значения следующих показателей производственно-хозяйственной деятельности предприятий машиностроения:
Т а б л и ц а 1 Исходная информация
Продолжение таблицы 1
МЕТОДИЧЕСКИЕ ВОПРОСЫ РАБОТЫ
Выбор варианта задания
В таблице 1 Например, студент в списке группы записан под номером 17. Исходные данные варианта 17: индекс У – 3; индексы Х – 4,8,12, т.е. из таблицы 1 нужно составить таблицу 3 исходных данных своего варианта. Т а б л и ц а 2 Варианты заданий
Т а б л и ц а 3 Исходные данные варианта 17
Таким образом, студенту необходимо выполнить корреляционно-регрессионный анализ следующих показателей: · · · · Содержание пояснительной записки: 1. Титульный лист (приложение 1). 2. Содержание. 3. Задание на работу. 4. Далее по каждому разделу корреляционно-регрессионного анализа: · краткие сведения из теории; · размещение информации на рабочем листе ЭТ; · результаты решения (вставка из Excel); · анализ полученных результатов. 5. Список использованной литературы. Оформление пояснительной записки Пояснительная записка – основной документ, предъявляемый студентом при защите работы. Она должна отражать основные этапы корреляционно-регрессионного анализа и полученные результаты. Общими требованиями к оформлению работы являются: · четкость и логическая последовательность изложения материала; · убедительность аргументации; · краткость и точность формулировок; · конкретность изложения результатов работы. Пояснительная записка готовится на украинском или русском языках в виде документа Word (формат А4 с книжной ориентацией листа; поля: сверху и снизу – 2,5 см, слева – 1,5 см, справа – 1,0 см; шрифт – 12 пт; абзацный отступ – 1,25 см; междустрочный интервал – одинарный; между словами делается один пробел). Графики, диаграммы и таблицы создаются в среде ЭТ с помощью мастера диаграмм и затем внедряются в документ. Для этой цели можно использовать и текстовый редактор. Иллюстрации должны быть пронумерованы в последовательности, соответствующей ссылкам в тексте. В тексте пояснительной записки используются только общепринятые сокращения слов. Формулы создаются с помощью редактора формул и нумеруются арабскими цифрами, заключенными в круглые скобки. Страницы нумеруются без пропусков, повторений и литерных добавлений. Текст записки делится на разделы и подразделы, которые нумеруются арабскими цифрами. Заголовки разделов и подразделов располагаются симметрично текста и выделяются полужирным стилем шрифта. Список использованной литературы оформляется аналогично тому, как это сделано в данной работе. Пояснительная записка должна быть сброшюрована. Следует иметь в виду, что небрежно оформленная работа студента может быть не допущена к защите. Защита работы Работа студента очной формы обучения сдается для проверки преподавателю, ведущему практические занятия, и после допуска к защите - защищается в процессе собеседования студента с этим преподавателем. Контрольная работа студента заочной и дистанционной формы обучения сдается для проверки на кафедру “Прикладная математика” и после допуска к защите - защищается в процессе собеседования студента с преподавателем, проверяющим работу. При этом студенту задаются любые вопросы по содержанию контрольной работы. При подготовке к защите работы следует использовать рекомендуемую литературу и данные методические указания. СОДЕРЖАНИЕ И ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ
1. Ввести многомерную выборку своего задания в смежный диапазон ячеек рабочего листа электронной таблицы (ЭТ). Результативный признак 2. Проверить исходную информацию на наличие грубых ошибок и выбросов. Необходимо обосновать каждую удаляемую строку многомерной выборки. 3. Для результативного признака построить гистограмму с помощью инструмента «Гистограмма» пакета анализа ЭТ и убедиться, что он подчиняется нормальному закону распределения. 4. Выполнить статистическую обработку многомерной выборки с помощью инструмента «Описательная статистика» пакета анализа ЭТ и проверить по значениям числовых характеристик подчинение всех признаков нормальному закону распределения. 5. С помощью инструмента «Корреляция» пакета анализа ЭТ получить корреляционную матрицу многомерной выборки. По корреляционной матрице выполнить анализ парной корреляции, т.е. установить по знакам коэффициентов парной корреляции наличие прямой или обратной связи. Кроме того, по абсолютной величине коэффициента парной корреляции оценить тесноту связи и выбрать наиболее значимый по тесноте связи с результативным признаком факторный признак. 6. Выполнить парный регрессионный анализ, включив в математическую модель регрессии результативный признак и выбранный в пункте 6 факторный признак. Параметры модели линейной и нелинейной регрессии получить с помощью инструмента «Регрессия» пакета анализа ЭТ. Оценить статистическую значимость уравнения линейной регрессии и его параметров по соответствующим критериям. Анализ качества нелинейной модели регрессии выполнить по критерию Фишера и коэффициенту парной корреляции. Определить точечный и интервальный прогноз на основе полученной модели регрессии, если ее можно использовать для прогнозирования. В ином случае проанализировать возможные причины несостоятельности модели регрессии. 7. Выполнить многомерный линейный регрессионный анализ с помощью инструмента «Регрессия» пакета анализа. В математическую модель регрессии включить независимые между собой факторные признаки. Оценить статистическую значимость уравнения регрессии и его параметров. Определить точечный и интервальный прогноз на основе полученной модели регрессии, если ее можно использовать для прогнозирования. В ином случае проанализировать возможные причины несостоятельности модели регрессии. 8. Выполнить многомерный нелинейный регрессионный анализ с помощью инструмента «Регрессия» пакета анализа. В математическую модель включить результативный признак и два независимых между собой наиболее значимых факторных признака. Оценить модель регрессии по критерию Фишера и коэффициенту парной корреляции. Определить точечный прогноз на основе полученной модели регрессии, если ее можно использовать для прогнозирования. В ином случае проанализировать возможные причины несостоятельности модели регрессии. 9. Выполнить прогноз на основе методов оптимизации – определить такие значения факторных признаков, которые обеспечивают заданное значение результативного признака КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ И КОМПЬЮТЕРНОЙ ТЕХНОЛОГИИ
Суть корреляционно-регрессионного метода состоит в том, что на основе имеющейся информации, полученной в результате статистических наблюдений за прошлое время, составляются уравнения регрессии, представляющие собой математические модели. Они могут быть линейными и нелинейными. По математическим моделям регрессии можно прогнозировать, т.е. находить прогнозные значения результативного признака при увеличении (уменьшении) значений входящих в модель регрессии факторных признаков на 10-15%. Уравнения регрессии в отличие от функциональных уравнений устанавливают зависимости между случайными переменными. Во время статистических наблюдений для каждого объекта часто можно измерить (получить) значения нескольких признаков. В итоге получается многомерная выборка. Смысл обработки многомерных выборок заключается в установлении связи между признаками. Для этого их делят на факторные и результативные. Факторный признак вызывает изменение других, связанных с ним, признаков. Результативный признак изменяется под действием факторных признаков. Связь может быть функциональной, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Если зависимость проявляется не в каждом отдельном случае, а в среднем при большом числе наблюдений, то она называется статистической (стохастической). В этом случае в расчетах используют среднее значение признака.Частным случаем статистической связи является корреляционная связь, при которой исследуется зависимость среднего значения результативного признака от факторных признаков.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Выполнить корреляционно-регрессионный анализ следующих показателей производственно-хозяйственной деятельности предприятий машиностроения: · · · · Определить прогнозируемые значения рентабельности на основе уравнений регрессии и методов оптимизации. Размещение информации для проведения корреляционно-регрессионного анализа представлено в таблице 7.
Т а б л и ц а 7 Размещение информации на рабочем листе ЭТ
Грубых ошибок и выбросов
Грубых ошибок в исходной информации многомерной выборки объемом
Т а б л и ц а 8 Контроль информации на наличие выбросов
Продолжение таблицы 8
В среде ЭТ с помощью мастера функций определяем для массива В отдельную ячейку заносим критическое значение этого критерия. Следовательно, первое экстремальное значение не является выбросом, т.е. в таком размере премии и вознаграждения на одного работника для рассматриваемой совокупности предприятий возможны. По расчетам второе экстремальное значение является выбросом. Поскольку речь идет о премиях и вознаграждениях, то возможно в современных условиях хозяйствования найдется предприятие, которое обеспечит своему персоналу получение хороших премий. Но для расчета второе экстремальное значение необходимо удалить.
Т а б л и ц а 11 Анализ результатов расчета. · Модель парной нелинейной регрессии
· Коэффициент парной корреляции · Расчетное значение критерия Фишера больше критического, следовательно, уравнение регрессии в целом статистически значимо и его можно использовать для прогноза. · Точечный прогноз: среднее значение рентабельности при По сравнению с линейной моделью регрессии среднее значение рентабельности увеличилось, но это значение находиться в границах интервального прогноза для линейной модели. Следовательно, в данном случае можно обойтись линейной моделью регрессии. Результаты расчетов свидетельствуют о том, что определять значения параметров нелинейной модели регрессии можно с помощью надстройки Поиск решения и инструмент Регрессия пакета анализа. Анализ результатов расчета. ¨ Уравнение многомерной нелинейной регрессии
¨ Коэффициент парной корреляции равен 0,718, т.е. связь между фактическими и теоретическими значениями результативного признака сильная. ¨ Критическое значение ¨ Расчетное значение критерия Фишера больше критического, следовательно, уравнение регрессии в целом статистически значимо и его можно использовать для прогноза. ¨ Точечный прогноз: среднее значение рентабельности предприятия при По данным выборки максимальное значение рентабельности равно 30,14. Следовательно, хорошим сочетанием значений признаков можно добиться лучших результатов, но принятые значения факторных признаков выходят за выборочные пределы значений этих признаков.
Целевая функция
Ограничения: Граничные условия: Результаты оптимизации представлены в таблице 22, размещение информации приведено в таблице 21.
Т а б л и ц а 21 Размещение информации на рабочем листе ЭТ
Примечание. В ячейку С6 записывается формула расчета целевой функции =СУММПРОИЗВ(a4:f4;a2:f2). Т а б л и ц а 22 Результаты оптимизации
Как видно из результатов расчета заданное значение рентабельности можно получить, если уменьшить непроизводственные расходы до 0,64 %, что реально сделать невозможно. Постановка задачи 2. Определить такие значения факторных признаков, которые обеспечат увеличение на 15 % максимальной выборочной рентабельности при условии, что непроизводственные расходы не превысят максимального выборочного значения.
Математическая модель Целевая функция
Ограничения: Граничные условия: Результаты оптимизации представлены в таблице 23.
Т а б л и ц а 23 Результаты оптимизации
Заданное значение рентабельности, равное 34,661, получено. Для этого необходимо предусмотреть возможность уве
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.110 (0.014 с.) |

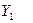 - производительность труда (среднегодовая выработка продукции на одного работника), тыс. грн.;
- производительность труда (среднегодовая выработка продукции на одного работника), тыс. грн.; - индекс снижения себестоимости продукции;
- индекс снижения себестоимости продукции; - рентабельность;
- рентабельность;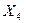 - трудоемкость единицы продукции;
- трудоемкость единицы продукции; - удельный вес рабочих в составе промышленно-производственного персонала (ППП);
- удельный вес рабочих в составе промышленно-производственного персонала (ППП); - удельный вес покупных изделий;
- удельный вес покупных изделий; - коэффициент сменности оборудования;
- коэффициент сменности оборудования; - премии и вознаграждения на одного работника, %;
- премии и вознаграждения на одного работника, %; - удельный вес потерь от брака;
- удельный вес потерь от брака; - фондоотдача,грн;
- фондоотдача,грн; - среднегодовая численность ППП, чел.;
- среднегодовая численность ППП, чел.; - среднегодовая стоимость основных производственных фондов (ОПФ), тыс. грн.;
- среднегодовая стоимость основных производственных фондов (ОПФ), тыс. грн.; - среднегодовой фонд заработной платы ППП, тыс. грн.;
- среднегодовой фонд заработной платы ППП, тыс. грн.; - фондовооруженность труда, грн.;
- фондовооруженность труда, грн.; - оборачиваемость нормируемых оборотных средств, дни;
- оборачиваемость нормируемых оборотных средств, дни; - оборачиваемость ненормируемых оборотных средств, дни;
- оборачиваемость ненормируемых оборотных средств, дни; - непроизводственные расходы, %.
- непроизводственные расходы, %.













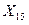


 являются результативными признаками, а
являются результативными признаками, а  - факторными признаками. При построении уравнений регрессии в качестве результативного признака выбирается один, указанный в таблице 2 под номером своего варианта.
- факторными признаками. При построении уравнений регрессии в качестве результативного признака выбирается один, указанный в таблице 2 под номером своего варианта.

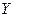 разместить после последнего факторного признака.
разместить после последнего факторного признака.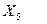 - удельный вес рабочих в составе промышленно-производственного персонала;
- удельный вес рабочих в составе промышленно-производственного персонала;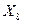 - премии и вознаграждения на одного работника, %;
- премии и вознаграждения на одного работника, %;
 нет, но среди элементов массива признака
нет, но среди элементов массива признака  имеется два элемента, значения которых резко выделяются на общем фоне: 0,03 и 4,44. Проверим, не являются ли эти значения выбросами. Результаты расчета представлены в таблице 8.
имеется два элемента, значения которых резко выделяются на общем фоне: 0,03 и 4,44. Проверим, не являются ли эти значения выбросами. Результаты расчета представлены в таблице 8.

 - критерия.
- критерия.
 т.е. связь между фактическими и теоретическими значениями результативного признака заметная.
т.е. связь между фактическими и теоретическими значениями результативного признака заметная. равно 29,242.
равно 29,242.
 при степенях свободы
при степенях свободы 


 равно 36,08.
равно 36,08.



















