
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка соответствия исследуемых признаков нормальному закону распределенияСодержание книги
Поиск на нашем сайте
Все основные положения теории корреляции и регрессии разработаны с учетом предположения о нормальном законе распределения исследуемых признаков. Если какой-либо признак не подчиняется нормальному закону распределения, то он не включается в математическую модель регрессии. Основой для выдвижения гипотезы о том, что случайная величина подчиняется нормальному закону распределения, может быть внешний вид гистограммы и значения числовых характеристик. Если близки по значению оценки выборочного среднего, моды и медианы, а оценки асимметричности и эксцесса незначительно отличаются от нуля, то случайная величина подчиняется нормальному закону распределения. Гистограмма строится для результативного признака с помощью инструмента «Гистограмма» пакета анализа. Для построения гистограммы следует установить курсор на свободную ячейку, войти в меню Сервис, выбрать операцию Анализ данных и в появившемся диалоговом окне выбрать инструмент пакета анализа Гистограмма. Если в меню Сервис отсутствует операция Анализ данных, то войти в Надстройки и загрузить Пакет анализа. Диалоговое окно «Гистограмма» приведено на рис.1. Гистограмму следует располагать на рабочем листе ЭТ с исходной информацией.
Рис. 1. Окно диалога инструмента Гистограмма Значения числовых характеристик для всех исследуемых признаков определяются с помощью инструмента «Описательная статистика» пакета анализа. Инструмент «Описательная статистика» позволяет получить значения 13 – ти статистических характеристик для десяти и более массивов переменных. Массивы на рабочем листе ЭТ должны быть размещены в смежном диапазоне ячеек, иметь одинаковую размерность и заголовки в первой строке. В таблице 5 представлены результаты обработки двух массивов.
Т а б л и ц а 5 Вывод итогов описательной статистики
Примечание. Функция МОДА возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных. Если множество данных не содержит одинаковых данных, то функция МОДА возвращает значение ошибки #Н/Д.
Для статистической обработки массивов следует выполнить последовательность операций Сервис · входной интервал – ввести диапазон ячеек, занимаемых элементами многомерной выборки вместе с заголовками; · указать метки в первой строке; · выходной интервал - указать адрес ячейки, начиная с которой будут размещаться результаты обработки; · обязательно щелкнуть мышью в квадратике «Итоговая статистика».
1.3. Корреляционный анализ статистических данных
Корреляционная зависимость проявляется достаточно отчетливо при большом числе наблюдений (закон больших чисел). Требования к исходной информации в соответствии с методологией корреляционного анализа: · рассматриваемые объекты выборки должны быть однотипными (например, предприятия, выпускающие однотипную продукцию); · выборка должна быть достаточно многочисленной; · для всех элементов выборки признак должен иметь одинаковую размерность и быть измерен с одинаковой точностью; · в математическую модель регрессии включаются независимые друг от друга факторные признаки, так как наличие тесной корреляционной связи между ними свидетельствует о том, что они характеризуют одни и те же стороны изучаемого явления и в значительной мере дублируют друг друга; · в математическую модель регрессии не включаются факторные признаки, функционально связанные с результативным признаком. Задачи корреляционного анализа: ¨ установление вида признака (количественный или качественный признак); ¨ установление наличия связи, направления действия и вида формы связи; ¨ выбор статистического показателя тесноты связи и определение его численного значения; ¨ установление статистической значимости тесноты связи и отбор факторного признака, который оказывает наиболее существенное влияние на результативный признак. Парная корреляция – это связь между двумя признаками, один из которых факторный, а другой – результативный или оба факторные. Парные корреляционные связи классифицируются по направлению действия и виду формы связи. По направлению действия корреляционная связь может быть: · прямой (положительной), при которой с увеличением (уменьшением) значения факторного признака увеличивается (уменьшается) значение результативного признака, а коэффициент корреляции положителен; · обратной (отрицательной), при которой с увеличением (уменьшением) значения факторного признака уменьшается (увеличивается) значение результативного признака, а коэффициент корреляции отрицателен. По виду формы связи различают корреляционную связь: · линейную (прямолинейную), при которой равномерному изменению значения факторного признака соответствует равномерное изменение значения результативного признака; · нелинейную (криволинейную), при которой с увеличением значения факторного признака происходит неравномерное увеличение (или уменьшение) значения результативного признака. Вид зависимости и формы связи легко установить по корреляционному полю точек. Для этого необходимо построить с помощью мастера диаграмм точечную диаграмму по табличным данным наблюдений. Если точки корреляционного поля: ¨ беспорядочно разбросаны по всему полю, то зависимости между исследуемыми признаками нет (рис.2 а); ¨ концентрируются вокруг прямой линии, идущей от нижнего левого угла в верхний правый угол, то имеется прямая линейная зависимость (рис.2 б); ¨ концентрируются вокруг прямой линии, идущей от верхнего левого угла в нижний правый угол, то имеется обратная линейная зависимость (рис.2 в); ¨ концентрируются вокруг некоторой кривой, то имеется нелинейная зависимость (рис.2 г, 2 д).
Рис.2. Связь корреляционного поля точек с выборочным коэффициентом корреляции Коэффициент парной корреляции характеризует тесноту связи между признаками X и Y в случае линейной зависимости. Теоретическое его значение определяется по формуле
где Корреляционный момент – это математическое ожидание произведения центрированных СВ Инструмент “Корреляция” пакета анализа (рис.3) позволяет вычислить корреляционную матрицу, содержащую коэффициенты парной корреляции многомерной выборки.
Рис.3. Окно диалога инструмента Корреляция Вид корреляционной матрицы представлен на рис.4.
Рис.4. Матрица коэффициентов парной корреляции
В реальных исследованиях чаще всего встречаются сложные взаимосвязи между явлениями, поэтому возникает задача определения тесноты связи между многими переменными. Для этой цели используют коэффициент множественной (многомерной) корреляции, который характеризует тесноту связи результативного признака с совокупностью факторных признаков. Проверка на тесноту связи. Если
Т а б л и ц а 6 Количественный критерий оценки тесноты связи
При анализе тесноты связи используют, кроме того, коэффициент детерминации, который при линейной связи равен квадрату коэффициента корреляции
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |



 Анализ данных
Анализ данных 
 , (2)
, (2) - корреляционный момент случайных величин (СВ) Х и Y;
- корреляционный момент случайных величин (СВ) Х и Y; 
 - среднеквадратичные отклонения СВ Х и Y.
- среднеквадратичные отклонения СВ Х и Y. и
и 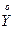 :
:  . Для независимых СВ
. Для независимых СВ  =0, следовательно, и
=0, следовательно, и  , в остальных случаях
, в остальных случаях  Оценкой теоретического коэффициента парной корреляции является выборочный коэффициент парной корреляции
Оценкой теоретического коэффициента парной корреляции является выборочный коэффициент парной корреляции  , который обладает свойствами коэффициента корреляции.
, который обладает свойствами коэффициента корреляции.
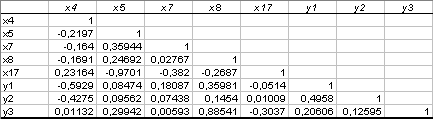
 , то связь между СВ Х и Y достаточно вероятна. Здесь
, то связь между СВ Х и Y достаточно вероятна. Здесь  - объем выборки. На практике чаще используют упрощенный критерий оценки тесноты связи, представленный в таблице 6.
- объем выборки. На практике чаще используют упрощенный критерий оценки тесноты связи, представленный в таблице 6.
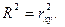 Коэффициент детерминации показывает долю изменения (вариации) результативного признака под влиянием факторного признака. Коэффициент детерминации принимает значения от 0 до 1.
Коэффициент детерминации показывает долю изменения (вариации) результативного признака под влиянием факторного признака. Коэффициент детерминации принимает значения от 0 до 1.


