
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прогнозирование на основе уравнения регрессииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Точечный прогноз получают путем подстановки в уравнение регрессии значений факторных признаков. Если полученная модель регрессии экономически объективна и обладает требуемой точностью, то прогнозируемые значения обладают достаточной надежностью. По своему характеру они являются средними значениями, которые следует ожидать с большой вероятностью. Значения отдельных данных наблюдений рассеиваются вокруг средних значений, поэтому фактические значения результативного признака не будут совпадать с расчетными (прогнозами). Рассеяние наблюдений вокруг линии регрессии определяет надежность получаемых по уравнению регрессии прогнозируемых оценок. Для каждого прогнозируемого точечного значения результативного признака необходимо определять доверительный интервал (интервальный прогноз)
где
Экономический смысл параметров модели регрессии
Значение регрессии Многомерный регрессионный анализ позволяет разграничить влияние факторных признаков. Параметр регрессии
1.8. Прогнозирование на основе методов оптимизации
Уравнение многомерной регрессии можно считать целевой функцией и использовать его при расчете прогнозов на основе методов оптимизации. Постановка задачи. Определить такие значения факторных признаков, которые обеспечивают увеличение (уменьшение) на 10-15 % максимального (минимального) значения результативного признака. Математическая модель задачи · Целевая функция
где · Ограничения:
где · Граничные условия: Так как целевая функция нелинейная, то имеем задачу нелинейного программирования. Для ее решения используется надстройка «Поиск решения». ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Выполнить корреляционно-регрессионный анализ следующих показателей производственно-хозяйственной деятельности предприятий машиностроения: · · · · Определить прогнозируемые значения рентабельности на основе уравнений регрессии и методов оптимизации. Размещение информации для проведения корреляционно-регрессионного анализа представлено в таблице 7.
Т а б л и ц а 7 Размещение информации на рабочем листе ЭТ
Контроль исходной информации на наличие Грубых ошибок и выбросов
Грубых ошибок в исходной информации многомерной выборки объемом
Т а б л и ц а 8 Контроль информации на наличие выбросов
Продолжение таблицы 8
В среде ЭТ с помощью мастера функций определяем для массива В отдельную ячейку заносим критическое значение этого критерия. Следовательно, первое экстремальное значение не является выбросом, т.е. в таком размере премии и вознаграждения на одного работника для рассматриваемой совокупности предприятий возможны. По расчетам второе экстремальное значение является выбросом. Поскольку речь идет о премиях и вознаграждениях, то возможно в современных условиях хозяйствования найдется предприятие, которое обеспечит своему персоналу получение хороших премий. Но для расчета второе экстремальное значение необходимо удалить.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.145 (0.01 с.) |

 (25)
(25) критическое значение
критическое значение  соответствует среднему значению результативного признака
соответствует среднему значению результативного признака  при заданном значении
при заданном значении  факторного признака
факторного признака  в предположении, что единственной причиной изменения результативного признака является этот факторный признак и отклонение
в предположении, что единственной причиной изменения результативного признака является этот факторный признак и отклонение 
 при каждом факторном признаке
при каждом факторном признаке  дает оценку его влияния на величину результативного признака
дает оценку его влияния на величину результативного признака 
 заданное значение результативного признака.
заданное значение результативного признака.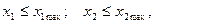
 максимальные значения факторных признаков в исследуемой выборке.
максимальные значения факторных признаков в исследуемой выборке.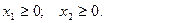
 - рентабельность;
- рентабельность;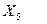 - удельный вес рабочих в составе промышленно-производственного персонала;
- удельный вес рабочих в составе промышленно-производственного персонала;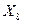 - премии и вознаграждения на одного работника, %;
- премии и вознаграждения на одного работника, %; - непроизводственные затраты, %.
- непроизводственные затраты, %.
 нет, но среди элементов массива признака
нет, но среди элементов массива признака  имеется два элемента, значения которых резко выделяются на общем фоне: 0,03 и 4,44. Проверим, не являются ли эти значения выбросами. Результаты расчета представлены в таблице 8.
имеется два элемента, значения которых резко выделяются на общем фоне: 0,03 и 4,44. Проверим, не являются ли эти значения выбросами. Результаты расчета представлены в таблице 8.

 - критерия.
- критерия.


