
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Парный нелинейный регрессионный анализСодержание книги Поиск на нашем сайте
Запишем в общем виде модель парной нелинейной регрессии
Для этого случая математическая запись метода наименьших квадратов имеет вид:
Определим параметры модели регрессии с помощью надстройки «Поиск решения». В качестве целевой функции принимаем выражение (30). Так как параметры модели регрессии могут принимать любые значения, то ограничения и граничные условия в математической модели оптимизации отсутствуют. Размещение информации представлено в таблице 13. Расчетные формулы записаны в таблицу 14.
Т а б л и ц а 13 Размещение информации на рабочем листе
Примечание. Символ = * означает, что в эту ячейку записывается формула, символ
Т а б л и ц а 14 Расчетные формулы
Примечание. В данном примере объем выборки равен 52, число неизвестных параметров регрессии – 3, из которых два связаны с факторным признаком, поэтому
Результаты расчета приведены в таблице 15.
Т а б л и ц а 15 Результаты расчета
Продолжение таблицы 15
Определим параметры модели регрессии с помощью инструмента Регрессия пакета анализа. Для оценки качества модели регрессии используем коэффициент парной корреляции и критерий Фишера. Выходная информация инструмента Регрессия и размещение информации приведены в таблице 16 и таблице 17.
Т а б л и ц а 16 Выходная информация инструмента Регрессия
Т а б л и ц а 17 Размещение информации
Коэффициент парной корреляции соответствует Множественному R регрессионной статистики таблицы 16. Анализ результатов расчета. · Модель парной нелинейной регрессии
· Коэффициент парной корреляции · Расчетное значение критерия Фишера больше критического, следовательно, уравнение регрессии в целом статистически значимо и его можно использовать для прогноза. · Точечный прогноз: среднее значение рентабельности при По сравнению с линейной моделью регрессии среднее значение рентабельности увеличилось, но это значение находиться в границах интервального прогноза для линейной модели. Следовательно, в данном случае можно обойтись линейной моделью регрессии. Результаты расчетов свидетельствуют о том, что определять значения параметров нелинейной модели регрессии можно с помощью надстройки Поиск решения и инструмент Регрессия пакета анализа. Многомерный линейный регрессионный анализ
Так как факторные признаки Математическая модель многомерной линейной регрессии:
Математическая запись метода наименьших квадратов:
Коэффициенты регрессии определяем с помощью инструмента «Регрессия» пакета анализа. Выходная информация представлена в таблице 18. Т а б л и ц а 18 Результаты работы инструмента «Регрессия»
Анализ результатов расчета: · Уравнение многомерной линейной регрессии
· Критическое значение · Критическое значение критерия Фишера равно 3,18. Расчетное значение критерия больше критического, следовательно, уравнение регрессии в целом статистически значимо. · Коэффициент детерминации меньше 0,5. Следовательно, среди неучтенных факторных признаков есть еще более существенные, которые необходимо включить в математическую модель многомерной регрессии. Так как один из параметров статистически не значим, то полученную модель нельзя использовать для прогнозирования, но можно использовать для расчетов внутри выборки.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 (29)
(29) (30)
(30)



















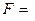

















 т.е. связь между фактическими и теоретическими значениями результативного признака заметная.
т.е. связь между фактическими и теоретическими значениями результативного признака заметная. равно 29,242.
равно 29,242. и
и  зависимы между собой, то их нельзя вместе вводить в математическую модель многомерной регрессии.
зависимы между собой, то их нельзя вместе вводить в математическую модель многомерной регрессии. (31)
(31) (32)
(32)


 - статистики равно 2,009. Для параметра модели регрессии при факторном признаке
- статистики равно 2,009. Для параметра модели регрессии при факторном признаке 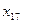 расчетное значение
расчетное значение 


