
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Демографические модели. Модель Мальтуса. Модель с взаимодействием по типу конкуренции за общий ресурс. Демографическая модель с дискретным временем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ДЕМОГРАФИЧЕСКИЕ МОДЕЛИ — математические модели, описывающие процессы воспроизводства и миграции населения. В частности: а) модели, в которых важную роль играет возрастная структура населения — другие его параметры рассматриваются как функции этой структуры (“демометрические функции”); б) демографические таблицы (таблицы рождаемости, смертности, плодовитости, количества браков и т. д.); в) модели воспроизводства населения, объединяющие таблицы смертности и плодовитости, широко применяемые для прогнозных и аналитических расчетов. Для изучения режима воспроизводства населения в зависимости от различных факторов используется также идеализированная модель “стабильного населения”. Получаемые с ее помощью данные могут вводиться в эконометрические модели (напр., в модели типа производственных функций). Демографические модели предназначены для описания преимущественно математическими методами населения и изменений в нем, процессов воспроизводства в целом или в отдельных его направлениях. Термин «моделирование» стал широко распространяться и применяться в демографии с 40-х гг. ХХ века. Модели в большинстве не охватывают всех процессов в многообразии сторон, учитывают лишь важнейшие характеристики явления. В частности, модели воспроизводства населения рассматривают дифференциацию населения по полу и возрасту, они абстрагируются от части признаков, которые рассматриваются как несущественные с позиции решаемых в модели задач. В основе модели лежит формализация объекта моделирования, который описывается набором количественных и качественных характеристик. Демографическое моделирование включает в себя набор эндогенных переменных – численность населения, число демографических событий, интенсивность их, темпы изменения, а также экзогенных – биологических, психологических, экономических и т.д. и обязательно – время. Во всех моделях в качестве экзогенной переменной используется длительность пребывания в данном демографическом состоянии, чаще всего возраст, учитываемый во взаимосвязи со временем; эндогенные переменные рассматриваются как функции длительного состояния или возраста – функции демометрические. Соотношение между переменными модели может быть представлено в виде математических формул, уравнений или их систем, числовых таблиц и т.д. Каждая модель строится в соответствии с твердо установленными правилами определения экзогенных переменных модели на основе данных статистики или других информационных материалов, а также правил интерпретации эндогенных переменных модели, толкования их значений. С каждой моделью соотносятся ограничения, которые определяют область применения модели, гипотезы, положенные в основу модели, соглашения, принятые при ее построении. Все это составляет обязательное условие использования моделей в демографическом анализе. Гипотезы – это содержательные предположения об особенностях объекта моделирования, они вытекают из конкретного демографического анализа. Соглашения – условные допущения, привносимые в модель, чтобы упростить ее математический аппарат, расчеты и т.д. Демографическая модель является абстрактной математической моделью, которая может отражать любое население, удовлетворяющее принятым ограничениям. Придавая переменным конкретные числовые или качественные значения, соответствующие конкретному населению на историческом этапе его существования, можно получить модель конкретного населения. Типовые модели представляют собой обобщение моделей конкретных населений. Значения переменных типовых таблиц отражают уже закономерности не какого-то конкретного населения, а любого населения или населения с некоторыми твердо установленными свойствами. Примером первых в демографической науке типовых моделей стали типовые таблицы смертности. Демографические модели, описывающие процессы на уровне всего населения или его частей, являются макромоделями, а описывающие процессы на уровне индивида через последовательность происходящих в его жизни событий – микромоделями. Модели делятся на стохастические (вероятностные) и детерминированные (большая часть макромоделей). Функциональная роль демографических моделей в современной науке широка: чтобы получить количественные характеристики демографических явлений; чтобы дать количественные оценки выявленных связей и зависимостей, проверить, таким образом, гипотезу; создать основу для демографического прогноза; используются для текущего и ретроспективного расчета, особенно тогда, когда отсутствуют статистические данные или они малодостоверны; для определения характера сбора и обработки информации о населении, в частности – перечня признаков индивида, дробности группировки; является полем мысленных демографических экспериментов, отработки методов демографического анализа, оценки последствий демографических событий, эффективности политики в области народонаселения.
Демографический прогноз использует ряд утвердившихся в науке методов. Одним из них является метод передвижки по возрастам – способ расчета на перспективу возрастно-половой структуры населения без учета влияния миграции. Перепись населения фиксирует численность людей в конкретной возрастно-половой группе (
Если умножить численность населения в возрастно-половой группе ( Общая схема перспективного расчета населения методом передвижки по возрастам выглядит так:
Другой метод – трендовая экстраполяция. Он употребляется при прогнозировании рождаемости, смертности, миграции в краткосрочном прогнозе. Метод экстраполяционного прогноза основан на методе экстраполяции рядов, используемых в статистике. Сложность применения этого метода состоит в том, что значение некоторых показателей может выходить за рамки допустимых значений (например, вероятность смерти оказывается отрицательной). В таком случае либо вводят дополнительные ограничения, либо прогнозируют не показатель, а некую однозначную функцию (так, вместо вероятности смерти прогнозируют ее логит-преобразование: logit, q = - ½ В основе следующего метода – прогноза по аналогии, или референтного прогноза, – лежит допущение, что динамика населения А, рассматриваемого в прогнозе, в будущем повторит динамику этого процесса в другом населении В, которое в своем демографическом развитии опережает население А. Теоретическая основа референтного метода – концепция демографического перехода, предполагающая переход от традиционного типа воспроизводства населения к современному. Методами прогноза является также использование социологических исследований, различных демографических моделей. Итак, демография как на теоретическом, так и на прикладном уровне служит основой для моделирования и прогнозирования демографических процессов
Модель Мальтуса Согласно модели, предложенной Мальтусом, скорость роста пропорциональна текущему размеру популяции, то есть описывается дифференциальным уравнением:
где
где Модель с взаимодействием по типу конкуренции за общий ресурс. Посмотрим, как ведет себя динамика при других начальных условиях. Видно, что общая закономерность остается такой же.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 3264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.008 с.) |

 ). Через год эта группа перейдет в следующую возрастную группу. В ней останутся все, за исключением той части, которая берется из таблиц смертности в виде коэффициента дожития (
). Через год эта группа перейдет в следующую возрастную группу. В ней останутся все, за исключением той части, которая берется из таблиц смертности в виде коэффициента дожития ( ):
): , где
, где  и
и  - числа живущих по таблице смертности.
- числа живущих по таблице смертности. ), то полученная величина и будет численностью населения через год в следующем возрасте (
), то полученная величина и будет численностью населения через год в следующем возрасте ( ).
).
 0
0

 =
=


 1
1
 =
=

 2
2
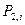 =
=


 3
3
 =
=

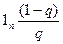 ).
). ,
, — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция
— некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция  . Если рождаемость превосходит смертность (
. Если рождаемость превосходит смертность ( ), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста:
), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста: ,
, — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению
— «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению 


