Триангуляционная модель поверхностей

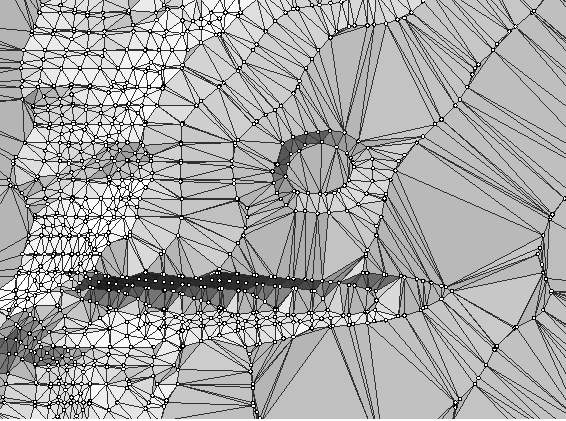
Триангуляционная модель данных (нерегулярная триангуляционная сеть, TIN) предназначена для описания поверхностей. В качестве моделируемой поверхности может выступать рельеф земной поверхности (рис. 2.10) или распределение какого-то параметра по земной поверхности, например, загрязнения окружающей среды, количества выпадающих осадков или среднегодовой температуры.

Заметим, что для моделирования поверхностей может использоваться и растровая модель, когда в каждом пикселе растра задается высота моделируемой поверхности. Однако триангуляционная модель имеет ряд преимуществ по сравнению с растровой. В первую очередь, это более высокая точность моделирования и обычно меньшие затраты памяти. Во-вторых, в триангуляционной модели можно в явном виде представлять резкие изломы поверхности, т.е. точки и линии, вдоль которых резко меняется кривизна поверхности (вершины гор, границы оврагов, обрывы рек, границы искусственных сооружений). В растровой модели предполагается, что вся моделируемая поверхность является гладкой поверхностью.

Исходными данными для построения триангуляционной модели поверхности служат высотные отметки, изолинии, а также различные структурные линии, меняющие форму поверхности.

В основе триангуляционной модели данных лежит триангуляция - особая структура данных из вычислительной геометрии, определенная на плоскости. В самом общем понимании триангуляция - это планарный граф, построенный на множестве заданных узлов и разбивающий всю плоскость на треугольники и одну внешнюю бесконечную фигуру.

 

Рис. 2.10. Триангуляционная модель поверхности Земли

 

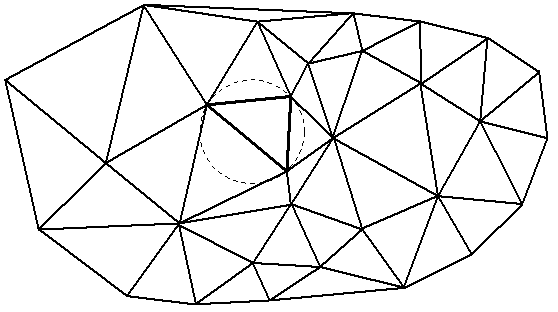
Триангуляция может быть различного вида. В триангуляционной модели данных используется так называемая триангуляция Делоне с ограничениями, в которой треугольники строятся так, чтобы они были «максимально равносторонними», а точнее так, что внутрь окружности, описанной вокруг любого треугольника, по возможности не должны попадать узлы триангуляции (рис. 2.11).

Так как триангуляция определена на плоскости, то для моделирования поверхностей (в частности, рельефа) в каждом узле триангуляции дополнительно добавляется еще одна координата - высотная отметка. При этом каждый треугольник триангуляции становится пространственным, определяя некоторую плоскую часть моделируемой поверхности.

Такие триангуляционные модели поверхностей обычно относят к классу так называемых 2,5-мерных моделей (ещё они иногда называются однозначными поверхностями двух переменных), подчеркивая, что, несмотря на наличие z -координат, это не полноценная 3-мерная модель, т.к. не любая поверхность может быть описана такой моделью. Например, в этой модели нельзя описать внутреннюю структуру пещеры и склоны горы, являющиеся вертикальными или имеющими отрицательный уклон. При этом на практике, при необходимости моделирования строго вертикальных граней (например, стен зданий) грани делают «почти» вертикальными, вводя дополнительные узлы в триангуляцию.

Рис. 2.11. Пример триангуляции Делоне с демонстрацией условия Делоне

 

Триангуляционная модель данных содержит 3 основных типа данных: узлы, ребра и треугольники (рис. 2.12).

Узлы в триангуляции характеризуются координатами .

Ребра в триангуляции являются отрезками, соединяющими два некоторые узла. Большинство рёбер в триангуляции в явном виде не представляются, т.к. их можно всегда косвенно получить через треугольники. В явном виде представляются только особые ребра, для которых нужно хранить дополнительную информацию, например, признак структурности линии или то, что поверхность не сохраняет гладкость вдоль этой линии.

 

Рис. 2.12. Связи объектов в триангуляционной модели данных

 

Треугольники в триангуляции описываются ссылками на 3 образующих узла, а также ссылками на смежные треугольники и особые ребра. Ссылки на смежные треугольники и ребра нужны только для ускорения операций анализа поверхности, а для отображения на карте не нужны.