Глава 6. Пространственный анализ

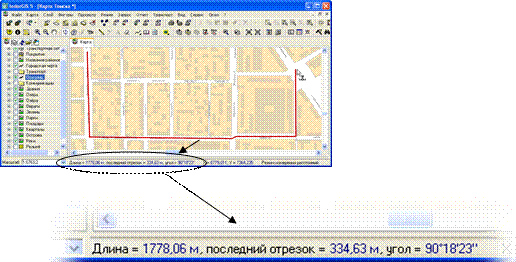
Измерительные операции

К измерительным операциям (картометрическим функциям) в ГИС относят функции, позволяющие определить различные геометрические характеристики объектов, явлений или пространства по карте (в проекции или по поверхности), такие как расстояния, площади, азимуты и др.

Все измерения в ГИС можно обычно выполнять двумя способами: а) указывая объекты, характеристики которых следует получить, и б) интерактивно задавая точки измеряемой геометрической фигуры.

Рассмотрим основные измерительные операции, которые можно выполнять в геоинформационных системах:

1. Определение координат точки на карте. Чтобы воспользоваться этой функцией в большинстве ГИС обычно не требуется переключаться в какой-то специальный режим работы. При перемещении мышки по карте, в строке статуса обычно показываются координаты указанной курсором точки. При этом в строке статуса может отображаться и высотная отметка этой точки, если в ГИС некоторая поверхность выбрана рабочей.

Координаты точек, отображаемые в ГИС, обычно показываются в исходных координатах объектов на карте (например, в градусах), однако возможно и в системе координат проекции (например, в метрах в проекции Гаусса-Крюгера).

2. Измерение расстояний, азимутов и углов. Пользователь должен указать на карте в ГИС последовательность точек ломаной, длину которой надо вычислить. ГИС выводит в строке статуса общую длину ломаной, а также длину последнего сегмента ломаной. Кроме того, для последнего сегмента может выводиться азимут и угол поворота относительно предыдущего сегмента (рис. 6.1).

3. Измерение площадей и периметров. Как и в предыдущем способе, пользователь должен задать в ГИС вершины некоторого многоугольника. При этом в строке статуса ГИС будет выводиться площадь и периметр.

4. Измерение линейных координат (пикета и смещения) точки относительно трассы. В этом режиме пользователь должен указать некоторую линию, относительно которой производится определение линейных координат. Далее, перемещая курсор мышки по карте, в строке статуса ГИС будет выводиться пикет и смещение указанной точки.

В заключение отметим, что некоторые геоинформационные системы предоставляют возможности по измерению расстояний и площадей с учетом формы земной поверхности. При этом вычисления могут происходить либо по поверхности референц-эллипсоида, либо по некоторой цифровой модели рельефа, заданной в виде регулярной или нерегулярной сети.

Рис. 6.1. Измерение расстояний

Векторный анализ

Под термином векторный анализ в геоинформатике подразумевается набор инструментов, позволяющих анализировать существующие геометрических объектов и строить новые.

Все операции векторного анализа определены над фигурами трёх типов: точечными, линейными и площадными.

В следующих подразделах мы рассмотрим различные виды операций векторного анализа и их применение на практике.

Анализ отношений

При анализе пространственных объектов часто возникают задачи поиска объектов, касающиеся друг друга, являющиеся смежными, вложенными, или состоящими в каких-то иных отношениях. Например, пусть задана некоторая автомобильная дорога на карте области. По карте земельных участков мы можем определить полосу отвода, в которой находится дорога, и соответствующую охранную зону. Далее мы можем найти все здания, попадающие внутрь соответствующей охранной зоны.

Все операции анализа отношений делятся на три группы:

А. Бинарные операции выявления отношений между парой заданных объектов. Результатом таких операций является логическое значение, определяющее, находятся ли два объекта в этом отношении или нет.

Б. Поисковые запросы, извлекающие все объекты из заданного набора пространственных данных, находящиеся в некотором бинарном отношении с указанным объектом. Результатом этой операции является множество объектов из заданного набора данных, удовлетворяющих указанному соотношению.

В. Операции пространственного соединения двух наборов пространственных данных. Результатом этой операции является множество пар объектов, удовлетворяющих некоторому заданному бинарному отношению, причем первые объекты в этих парах должны принадлежать первому набору пространственных данных, а вторые объект - второму.

Всего выделяют 8 основных видов бинарных отношений между пространственными объектами. Далее мы их рассмотрим, а для каждого из них будут приведем рисунки, комментирующие их для 3 основных типов (в зависимости от размерности) векторных данных: точечных (0-мерных), линейных (1-мерных) и площадных (2-мерных). Для некоторых сочетаний типов фигур описываемые операции не имеют смысла.

Каждое рассматриваемое отношение имеет два аргумента, которые на рисунке обозначены как «Первая фигура» и «Вторая фигура», соответственно, на пересечении размещается пример отношения. Все отношения имеют названия в форме глагола (возможно с последующим предлогом), например, «Содержит в себе», поэтому отношение следует читать по следующему шаблону: «Первая фигура содержит в себе вторую фигуру».

Итак, рассмотрим эти отношения:

1. Отношение «Совпадает с» (Equals). Две фигуры находятся в этом отношении, если они совпадают между собой (рис. 6.2). При этом фигуры считаются совпадающими, если все узловые точки фигур (ломаных или полигонов) имеют совпадающие координаты. Отношение определено только для фигур, имеющих одинаковую размерность.

2. Отношение «Содержит в себе» (Contains). Две фигуры находятся в этом отношении, если вторая фигура находится внутри первой, при этом ни одна точка второй фигуры не должна находиться вне первой (рис. 6.3). Отношение не определено в случае, когда вторая фигур имеет большую размерность, чем первая.

3. Отношение «Содержится в» (Within, Inside). Две фигуры находятся в этом отношении, если первая фигура находится внутри второй, при этом ни одна точка первой фигуры не должна находиться вне второй (рис. 6.4). Отношение не определено в случае, когда вторая фигур имеет меньшую размерность, чем первая.

Вариантом этого отношения является «Полностью содержится в» (Covered By), когда первая фигура не может пересекать границу второй.

Рис. 6.2. Отношение «Совпадает с» (Equals)

 

Рис. 6.3. Отношение «Содержит в себе» (Contains)

 

4. Отношение «Пересекается с» (Crosses). Отношение определено только между линейными и площадными объектами, при этом хотя бы одна фигура должна быть линией. Если обе фигуры являются площадными, то такое отношение называется «Накладывается на» и рассматривается ниже. Две фигуры находятся в этом отношении, если эти фигуры имеют общие точки, т.е. две линии должны иметь точку пересечения, а линия и полигон должны пересекаться по некоторой линии (рис. 6.5).

 

Рис. 6.4. Отношение «Содержится в» (Within)

 

 

Рис. 6.5. Отношение «Пересекается с» (Crosses)

 

 

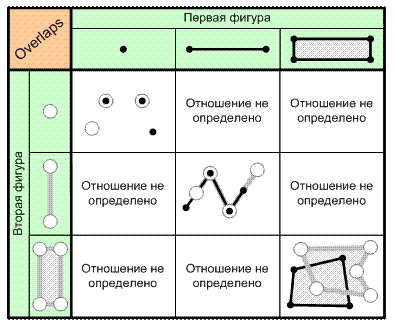
5. Отношение «Отделена от» (Disjoint). Две фигуры находятся в этом отношении, если обе фигуры не имеют общих точек.

6. Отношение «Перекрывается с» (Overlaps). Две фигуры находятся в этом отношении, если область пересечения этих фигур имеет ту же размерность, что и сами фигуры, т.е. эти фигуры имеют общие внутренние точки (рис. 6.6). Отношение определено только для фигур, имеющих одинаковую размерность.

7. Отношение «Граничит с» (Touches). Две фигуры находятся в этом отношении, если эти фигуры соприкасаются только своими границами, но не своими внутренними областями, т.е. ломаные могут касаться только своими вершинами, а полигоны - своими контурами. Отношение не определено только для двух точечных фигур.

 

Рис. 6.6. Отношение «Перекрывается с» (Overlaps)

 

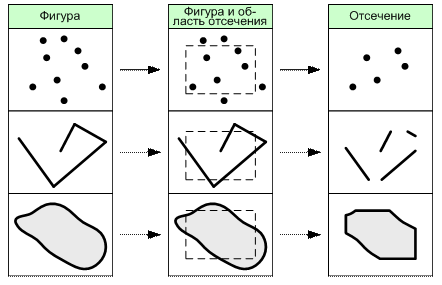
8. Отношение «Касается» (Any Interacts). Две фигуры находятся в этом отношении, если эти фигуры имеют общие точки.

Помимо бинарных отношений, существуют и иные отношения, например, такое тернарное (аргументами в котором являются две фигуры и некоторый параметр) как «На расстоянии» (Distance). В различных вариантах этого отношения требуется, чтобы расстояние между ближайшими точками двух фигур было равно, менее, более, не более или не менее заданной величины.

Как было сказано выше, в поисковых запросах из заданного набора данных извлекаются все фигуры, находящиеся в некотором бинарном отношении с указанной фигурой. Однако наиболее часто на практике используются следующие виды запросов (особенно при интерактивном выделении объектов на карте):

1. Поиск фигур, вложенных в заданный прямоугольник, круг или произвольный многоугольник. Найденные объекты должны целиком помещаться внутри заданной фигуры.

2. Поиск фигур, пересекающихся с заданным прямоугольником, кругом или произвольным многоугольником. Найденные фигуры должны полностью или хотя бы частично помещаться внутри заданной фигуры.

Также отметим, что среди всех возможных операций соединения наиболее часто используются следующие:

1. Поиск всех пар вложенных многоугольников среди двух множеств многоугольников, когда многоугольник из первого множеств должен войти в многоугольник из второго множества.

2. Поиск всех пар пересекающихся многоугольников среди двух множеств многоугольников, когда многоугольник из первого множеств должен пересечься с некоторым многоугольником из второго множества.

В заключение отметим, что проверки отношений фигур всегда выполняются с некоторой заданной величиной допуска, при этом точки, координаты которых отличаются на величину, меньшую заданного допуска, считаются совпадающими.

Отсечение и разрезание

Операция отсечения позволяет удалить части пространственного объекта, лежащие вне области отсечения. При этом части, лежащие на границе области отсечения, считаются попадающими внутрь области, а потому не отсекаются. В качестве области отсечения может выступать любой площадной объект, но обычно используются прямоугольники и одноконтурные многоугольники, реже - произвольные многоконтурные многоугольники и круги.

Операция отсечения может быть применена для пространственных объектов любой размерности. Если исходный объект целиком содержится в области отсечения, то операция возвращает исходный объект без изменений. Иначе, отсекая некоторые части исходного, создаётся новый пространственный объект, который целиком содержится в области отсечения. При этом из-за отсечения от объекта может вообще ничего не остаться, и поэтому операция отсечения не возвратит пустой объект. Если новый объект будет иметь меньшую размерность, чем исходный, то операция отсечения также ничего не возвратит. Иначе операция отсечения возвратит новый объект, имеющий ту же размерность, что и исходный объект.

На рис. 6.7 приведён пример выполнения операции отсечения для фигур различного вида. В качестве примера 0-мерных (точечных) объектов используется мультиточка - фигура, состоящая из нескольких точек.

В ГИС операция отсечения обычно реализована следующим образом. Пользователь выделяет некоторые объекты на карте и выбирает команду отсечения. Затем ГИС предлагает пользователю интерактивно указать на карте область отсечения (прямоугольник, многоугольник, окружность), после чего у выделенных фигур ГИС отсекает части, лежащие вне заданной области.

Операция разрезания во многом похожа на отсечение. Эта операция позволяет разрезать некоторый линейный или площадной объект вдоль заданной ломаной, которая не должна самопересекаться. Результатом операции разрезания являются отрезы слева и справа - части исходного объекта, оказавшиеся по разные стороны от линии разреза (рис. 6.8).

 

Рис. 6.7. Операция отсечения пространственных объектов

 

Рис. 6.8. Операция разрезания пространственных объектов

 

В ГИС операция разрезания обычно реализована следующим образом. Пользователь выделяет некоторые объекты на карте и выбирает команду отсечения. Затем ГИС предлагает пользователю интерактивно указать на карте ломаную разрезания, после чего выделенные фигуры ГИС разрезает на части, лежащие слева и справа от заданной ломаной.

Оверлейные операции

Оверлейные операции (операции наложения, картографической алгебры, алгебры карт) позволяют вычислять объединения, пересечения или разности отдельных пространственных объектов или сразу двух множеств объектов. Оверлейные операции определены для пространственных объектов всех размерностей, но в одной операции могут участвовать только объекты одной размерности. Результатом операции является новый объект, имеющий ту же размерность, что и исходные объекты, либо пустое множество. Иногда в результате формального выполнения правил оверлейных операций могут возникать фигуры меньшей размерности (например, область пересечения двух граничащих фигур является линией или точкой), чем исходные, но такие фигуры отбрасываются, и считается, что операция возвращает пустое множество.

Результатом операции объединения двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат хотя бы одному исходному объекту (рис. 6.9).

 

Рис. 6.9. Операция объединения пространственных объектов

 

Результатом операции пересечения двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат обоим исходным объектам.

Результатом операции разности двух пространственных объектов является объект, состоящий из всех точек плоскости, которые принадлежат первому объекту, но не принадлежит второму (рис. 6.10).

Результатом операции симметрической разности двух объектов является объект, состоящий из всех точек плоскости, которые принадлежат первому или второму объекту, но обоим сразу.

Операции построения объединения, пересечения и разности линий и многоугольников имеются во многих графических программах, не являющихся ГИС. Однако в ГИС мы имеем дело не просто с геометрическими фигурами, а пространственными объектами, которые помимо геометрической составляющей ещё имеют атрибуты. Именно поэтому после выполнения оверлеев новые объекты должны иметь атрибуты, значения которых формируются на основе исходных объектов. Новый набор атрибутов обычно является объединением наборов атрибутов исходных объектов. При этом значения новых атрибутов определяются на основании значений исходных атрибутов одним из двух следующих способов:

1. Значение атрибута просто копируется из исходного объекта. Если этот атрибут был в обоих исходных объектах, то берётся атрибут из того объекта, площадь которого больше. Такой способ используется, если в атрибуте хранятся не числа (строки, дата, время, логические значения) или числа, не имеющие непрерывную интерпретацию (например, код типа земельных угодий).

2. Значение атрибута меняется пропорционально изменению площади нового объекта по отношению к исходному.

Рис. 6.10. Операция разности пространственных объектов