Буферные зоны, оболочки, зоны близости

Буферная зона вокруг фигуры F - это наибольшая область на карте, все точки внутри которой удалены от F не более чем на заданное расстояние L (рис. 6.11). При построении в ГИС буферных зон расстояние L может быть задано заранее, либо вычисляться динамически для каждого объекта отдельно на основе его атрибутов. Некоторые ГИС позволяют за раз построить для каждого объекта не одну буферную зону, а сразу несколько кольцевых буферных зон. Например, указав и что нужно построить по 3 зоны, будут созданы 3 области, в первой из которых расстояние l от любой точки до исходного объекта будет , во второй , а в третьей .

Буферные зоны используются в геоинформатике, например, для моделирования полос отведения вдоль дорог, санитарных зон вокруг рек и озер, охранных зон вдоль линий газопроводов и линий электропередачи, оценки областей неблагоприятного воздействия на человека вокруг различных источников.

Выпуклая оболочка множества объектов F - это наименьшая выпуклая область на карте, содержащая все объекты F. Оболочка может быть построена по объектам любой размерности, но результатом в ГИС всегда является полигон.

В задаче построения зон близости требуется найти все точки плоскости, для которых расстояние s до заданного множества объектов является минимальным. В случае, когда все объекты являются точками, данная задача известна как задача построения диаграмм Вороного.

 

Рис. 6.11. Операция построения буферной зоны

 

Операция построения зон близости может использоваться, например, для нахождения зон скорейшего обслуживания (зон близости) из заданных базовых пунктов. Пусть, например, в некоторых точках на территории региона расположены аэродромы с пожарными вертолётами. В случае возникновения лесного пожара, по заданной точке его локализации мы определяем зону близости, а, следовательно, и вертолёт, который быстрее всех сможет долететь до места пожара.

Приведенный пример предполагает одинаковые скорости перемещения вертолётов, но в действительности они могут отличаться, также могут отличаться и удельные затраты на перемещение.

В операции построения взвешенных зон близости требуется определить все точки плоскости, для которых расстояние s до заданного множества объектов , помноженное на веса , является минимальным.

Для нашего примера укажем скорости полёта вертолётов в качестве весов . Полученные взвешенные зоны близости приведены на рис. 6.12.

Под термином генерализация в геоинформатике понимается набор операций обобщения, предназначенных для отображения пространственных данных в соответствии с заданным масштабом, содержанием и тематикой карты. В самом распространенном случае генерализация позволяет уменьшить количество и упростить состав пространственных объектов при заданном уменьшении масштаба карты (рис. 6.13).

 

Рис. 6.12. Операция построения взвешенных зон близости

 

Рис. 6.13. Операция генерализации

 

Генерализация

 

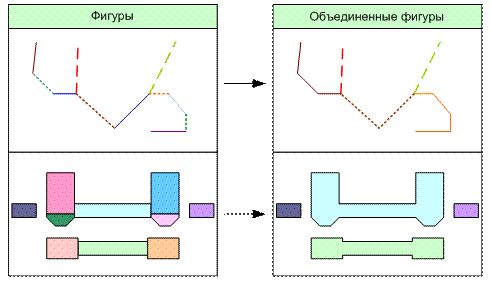
Рассмотрим основные операции генерализации при работе с векторными объектами. При этом сразу отметим, что не все из нижеприведенных операций реализованы в современных ГИС, т.к. многие операции четко не формализованы и потому не могут быть алгоритмизированы. Именно поэтому процесс генерализации в ГИС по-прежнему требует много творческой интерактивной работы пользователя.

1. Упрощение. Эта операция изменяет внутреннюю геометрическую структуру линии или полигона, удаляя некоторые точки (например, почти совпадающие, а также последовательные точки, лежащие почти на одной прямой) исходя из заданного геометрического критерия.

2. Сглаживание. Эта операция сдвигает некоторые точки линий и границ полигонов с целью устранения мелких нарушений и выделения наиболее значимых тенденций изменения фигуры.

3. Сдвиг объектов. Эта операция немного (в пределах заданной величины) перемещает целые объекты с целью избежания слияния или наложения объектов при уменьшении масштаба.

4. Чистка (удаление мелких объектов). Эта операция удаляет линейные и площадные объекты, размеры которых меньше некоторого установленного минимума.

5. Адаптивная чистка. Эта операция удаляет с карты объекты любой размерности, которые накладываются друг на друга и имеют самую низкую «важность». Эта операция реализуется с помощью «жадного» алгоритма. Вначале всем объектам, которые потенциально разрешено удалять, присваиваются некоторые веса (важности объектов), и все эти объекты сортируются в порядке убывания весов. Затем объекты по очереди помещаются на карту, начиная с самого важного. Если изображение очередного добавляемого на карту объекта сливается с ранее помещенными объектами, то такой объект отбрасывается.

Покажем использования адаптивной чистки на примере населенных пунктов на карте России. Пусть мы хотим разместить населенные пункты вместе с их названиями, причем названия должны быть разного размера. В качестве веса населенного пункта будем использовать численность его населения. В итоге, после адаптивной чистки, в западной части России на карте останутся только крупные города, а на востоке, в малонаселенных районах, - даже деревни.

6. Слияние близких и граничащих объектов. Эта операция уменьшает общее число объектов на карте за счет объединения близких фигур. Объединяться могут фигуры, которые строго граничат друг с другом (рис. 6.14) либо которые расположены достаточно близко друг к другу (например, две близкие параллельные дороги).

7. Снижение размерности. Эта операция заменяет маленькие многоугольники линиями или точками, а маленькие линии - точками (см. рис. 6.14). Например, на крупномасштабной карте населенные пункты и озёра могут показываться своими контурами, а на мелкой карте - точками. На крупной карте реки зачастую показываются областями с границами по линиям уреза воды, а мелких картах - осевыми линиям. На крупной карте мосты и тоннели на автомобильной дороге могут быть показаны в виде линий, являющих частью дороги, а на мелкомасштабных картах - в виде точек на осевой линии дороги.

8. Оконтуривание групп отдельных объектов. Эта операция применяется, например, для замены множества отдельно стоящих деревьев на области, обозначаемые как парки или зеленые насаждения (см. рис. 6.13).

 

Рис. 6.14. Операция объединения граничащих фигур

 

9. Корректировка (текстурирование). Эта операция предназначена для внесения некоторых дополнительных точек в линии и полигоны для придания внешнему виду фигур натуральности. Например, река может быть представлена на карте гладкой осевой линией, однако при этом мы знаем, что на самом деле река очень извилиста, но эти извилины совершенно не видны в масштабе карты. Такие небольшие извилины можно принудительно создать с помощью данной команды.

Теперь кратко рассмотрим некоторые аспекты генерализации объектов, представленных в других моделях данных, нежели в векторных.

Генерализации растровых данных обычно сводится только к уменьшению размера растра и интерполяции значений пикселей нового растра на основе исходного. Например, при уменьшении размера растра по высоте и ширине в 4 раза, каждый новый пиксель должен быть вычислен на основе значений 16 исходных.

Если в исходном растре в пикселях хранились числовые непрерывные данные, то значения пикселей в новом растре просто усредняются на основе исходных значений. В остальных случаях в качестве значения обычно выбирается то значение, которое наиболее часто представлено в исходных пикселях.

В результате генерализации триангуляционных поверхностей строится новая поверхность с меньшим количеством узлов триангуляции, которая отличается от исходной поверхности не более, чем на заданную величину. В процессе генерализации поверхности может выполняться 3 вида упрощений: удаление узлов, замена коротких рёбер и небольших треугольников триангуляции одним узлом.