
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Структура и источники геоданныхСодержание книги
Поиск на нашем сайте
Системы координат Основная цель введения некоторой системы координат в геоинформатике - это описание положения объектов на поверхности Земли в некотором «естественном» виде. Если мы хотим определить положение судна в океане, и нам нужно проложить маршрут движения по карте, то вначале мы «естественно» должны определить широту и долготу положения судна в градусах с помощью специальных приборов. При этом мы используем географические координаты. Применение таких координат удобно с точки зрения их понимания и вычисления различными астрономическими методами, однако крайне неудобно для выполнения любых геометрических измерений и построений. Например, очень сложно определить кратчайшее расстояние между двумя пунктами на поверхности Земли, положения которых заданы в градусах. Это связано с тем, что поверхность Земли не является плоскостью, а поэтому формулы вычисления расстояний и других геометрических измерений на реальной поверхности Земли крайне сложны. В связи с тем, что физическая поверхность Земли имеет очень сложную форму, она в зависимости от решаемых задач аппроксимируется некоторой фигурой, достаточно просто описываемой математически, например, сферой или эллипсоидом. Это позволяет разработать формулы для определения того же самого расстояния на поверхности сферы. Однако если мы строим новый квартал в городе, то «естественно» предположить, что поверхность Земли в пределах застраиваемой территории является плоской, а потому все сложности сферической геометрии можно отбросить и использовать привычные для всех со школы формулы геометрии на плоскости. Именно поэтому проект внутриквартальной застройки «естественно» выполнить на топографическом плане, используя прямоугольные декартовые координаты в пространстве. При этом важнейшим вопросом является выбор этой декартовой системы координат. «Естественно» предполагать, что ось Z этой системы координат должна быть направлена вверх, а другие оси - параллельно поверхности Земли в начале координат. Это нужно для того, чтобы можно было в полевых условиях измерять высоты на местности с помощью нивелира, а также определять вертикали с помощью обычного отвеса. В тоже время, если мы строим большой протяженный объект, например, дорогу, протянувшуюся на сотни или тысячи километров, то поверхность Земли на таких расстояниях будет существенно отличаться от плоскости. Отклонение поверхности Земли от касательной плоскости, в которой определена декартова система координат, составляет на расстоянии 1 км от точки касания 7,8 см, а на 10 км - уже 7,84 м! Поэтому проект строительства дороги будет разбит на участки, выполняемые в различных декартовых системах координат. Основной проблемой такого способа является стыковка участков проекта, выполненных в разных локальных системах координат. Таким образом, возникает необходимость выработки общего подхода, позволяющего легко и непротиворечиво получать локальные системы координат, взаимно увязывать их друг с другом, а также при необходимости переходить к географическим координатам.
Для этого нужно построить некую модель поверхности всей Земли, а также определить формулы перехода от этой модели к локальным координатам. «Естественно» предполагать, что все локальные (местные) декартовые системы координат должны иметь 1) начала координат, лежащие на модели поверхности Земли, 2) ось Z, направленную по нормали к поверхности. При таких предположениях, по крайней мере, измерение вертикали в локальной системе координат можно будет производить на местности с помощью обычного отвеса. Отсюда возникают следующие понятия. Определение. Уровенной называется поверхность, ортогональная в каждой своей точке к векторами силы тяжести. Определение. Геоидом называется уровенная поверхность, проходящая через некоторую точку начала отсчета высот. Однако геоид имеет крайне сложную форму и её практически невозможно математически точно описать. Поэтому, в зависимости от решаемых задач, форма геоида может аппроксимироваться сферой, эллипсоидом вращения, трехосным эллипсоидом или, наиболее точно, квазигеоидами. Сложность формы геоида (как и любой другой уровенной поверхности) возникает из-за того, что Земля состоит из неравномерно распределенных масс различной плотности. Это приводит к тому, что сила тяжести на поверхности Земли в разных местах является различной. Кроме того, вектора силы тяжести направлены в самые разные направления, не сходящиеся в центре масс Земли.
Определение. Общеземным называется эллипсоид вращения, плоскость экватора и центр которого совпадают с плоскостью экватора и центром масс Земли, и наилучшим образом описывают поверхность геоида. Определение. Референц-эллипсоидом (референц-сферой) называется такой эллипсоид (сфера), который наилучшим образом аппроксимирует поверхность геоида на соответствующей территории Земли. Определение. Квазигеоидом называется такая фигура, которая на различных участках поверхности Земли аппроксимируется различными местными референц-эллипсоидами. На территории морей и океанов поверхность квазигеоида совпадает с поверхностью геоида, а на суше она отклоняется от него в пределах двух метров. Большинство референц-эллипсоидов являются эллипсоидами вращения, которые характеризуются длинами своих полуосей (a - расстояние от его центра до точек экватора и b - расстояние от центра до полюсов) и вытекающим из этих длин коэффициентом сжатия
Рис. 3.1. Эллипсоид вращения
Кроме своих размеров референц-эллипсоиды характеризуются положением центра в теле Земли и ориентацией вертикальной оси. Когда для работы на территории берется некоторый местный референц-эллипсоид, то он выбирается так, чтобы максимально точно соответствовать поверхности геоида на этой территории (рис. 3.2). Именно поэтому данный референц-эллипсоид может очень сильно отличаться от поверхности геоида на других территориях. Среди множества имеющихся в мире референц-эллипсоидов в России наиболее часто используется эллипсоид Красовского (
Рис. 3.2. Аппроксимация поверхности Земли референц-эллипсоидами
В России с 1 июля 2002 г. обязательным к применению является система координат СК-95 (на основе эллипсоида Красовского, но несколько смещенного и повернутого относительно СК-42) для всех геодезических и картографических работ, а для геодезического обеспечения орбитальных полетов - ПЗ-90 (Параметры Земли 1990 г.), имеющая параметры Тем не менее, в последнее время в России все чаще стал также применяться референц-эллипсоид WGS-84 ( В математической картографии используются пространственные прямоугольные, криволинейные, плоские прямоугольные и полярные системы координат. Самой простой является пространственная прямоугольная геоцентрическая система координат, начало которой совмещено с центром Земли, ось Z направлена на Северный полюс Земли, ось X - на точку пересечения Гринвичского меридиана с экватором, а ось Y - на восток от Гринвича (рис. 3.3). В качестве точки Северного полюса обычно используют условный земной полюс (международное условное начало), которая вместе с центром масс Земли определяет некоторое фиксированное среднее положение оси вращения Земли. Это связано с тем, что ось вращения Земли со временем перемещается в теле Земли и относительно звезд.
В то же время на практике обычно используются различные квазигеоцентрические системы координат, центр которых и угол наклона осей несколько иной. Именно поэтому имеются специальные формулы для пересчета координат из одной системы координат в другую:
где
Рис. 3.3. Геоцентрическая система координат
Ориентация используемого референц-эллипсоида характеризуется смещением от центра масс Земли и отклонением его оси относительно оси вращения Земли. Однако более привычной является географическая (геодезическая) система координат, когда координаты точки на поверхности эллипсоида определяются широтой Использование вышеприведенных геоцентрической и географической систем координат не всегда удобно. Так, при работе на небольших участках земной поверхности обычно используется топоцентрическая (горизонтная) система координат, которая является обычной прямоугольной пространственной системой координат и характеризуется некоторой начальной точкой
Рис. 3.4. Географическая (геодезическая) система координат
Рис. 3.5. Топоцентрическая (горизонтная) система координат
Все вышеприведенные системы координат предназначены для задания «абсолютных координат», т.е. координат, не зависящих от положения никаких объектов в пространстве. В противовес абсолютным часто используются различные относительные координаты, в которых отсчет ведется от некоторых заметных объектов на местности.
Относительные системы координат бывают двух основных видов: 1. Относительная полюсная система координат. В этих координатах отсчет ведется от полюсов - некоторых известных точек на местности, заданных либо в абсолютной системе координат, либо в описательном виде. Положение любой иной точки на местности может задаваться как азимут и расстояние от некоторого полюса, либо как расстояния от двух полюсов. С помощью таких координат очень часто задается положение объектов подземных инженерных коммуникаций (колодцев, труб, кабелей) на картах местности, например, в терминах «4 метра на север от угла дома» или «в 5 метрах от угла дома и на расстоянии 6 метров от стены трансформаторной подстанции» (рис. 3.6).
Рис. 3.6. Задание положения инженерных коммуникацией с помощью относительной полюсной системы координат
Эта система координат позволяет задать положение объектов на плане, а также в пространстве, добавляя в описание координат смещение по высоте искомой точки от плановой («2 метра под землей») или от базовой точки («3 метра ниже отметки на стене дома»). 2. Относительная линеаризованная (пикетажная) система координат. В этой системе за основу берется некоторая базовая кривая, положение которой задано в абсолютной системе координат. Кроме того, на этой кривой выбирается некоторая базовая точка B (обычно это начало кривой). Положение любой иной точки C на базовой кривой считается как кратчайшее расстояние от этой точки до базовой точки вдоль базовой кривой. Такое расстояние часто называют пикетажным расстоянием или пикетажем. Для определения положения любой точки P на плоскости, не лежащей на базовой прямой, нужно найти ближайшую точку С на базовой прямой. Положением точки P будет считаться пара величин «пикетаж + смещение», где «пикетаж» - это пикетаж точки С относительно B, а «смещение» - это расстояние от P до C. Причем, если точка P располагается справа от кривой BC, то смещение берется со знаком плюс, иначе - со знаком минус (рис. 3.7).
Рис. 3.7. Задание положения объектов инженерного обустройства автомобильной дороги с помощью линеаризованной системы координат Картографические проекции В связи с тем, что форма Земли не является плоской, при построении бумажных или электронных карт используются так называемые картографические проекции - математические способы отображения поверхности Земли на плоскость. К настоящему времени создано огромное количество различных проекций, выбор которых для применения зависит от размеров картографируемой территории, назначения карты, а также стандартов, принятых в той или иной стране. Одной из важнейших характеристик проекций является характер и величина искажений. При этом выделяют следующие виды проекций: 1. Равноугольные проекции. В этих проекциях сохраняются без искажений углы и формы малых объектов, но сильно искажаются длины и площади объектов. В математике такие преобразования называются конформными. Такие проекции используются, например, для навигации и прокладки транспортных маршрутов.
2. Равновеликие проекции. Эти проекции сохраняют площади всех объектов, но искажают углы и формы объектов. В таких проекциях очень удобно, например, определять площади земельных участков. 3. Равнопромежуточные проекции. В этих проекциях сохраняются длины вдоль одного из главных направлений (обычно вдоль параллелей либо вдоль одного или всех меридианов). 4. Произвольные проекции. В таких проекциях не сохраняются длины, площади или углы, однако преобразование проекции подбирается так, чтобы искажения углов, площадей и длин были в целом по карте минимальны. Обычно в центре карты делают минимальные искажения, которые плавно возрастают к краям. Картографические проекции обычно задаются в виде:
где x - вертикальная (не горизонтальная!) координата после проецирования; y - горизонтальная координата; 1. Цилиндрические проекции. В этих проекциях меридианы - это равноотстоящие параллельные линии, а параллели - параллельные прямые, ортогональные меридианам. Общие уравнения цилиндрических проекций:
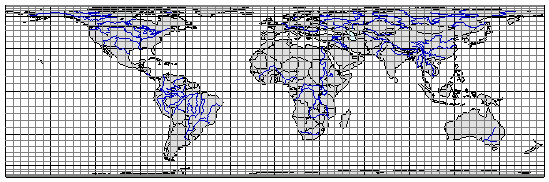
где c - постоянный параметр. На рис. 3.8 приведен пример равновеликой цилиндрической проекции.
Рис. 3.8. Равновеликая цилиндрическая проекция
2. Псевдоцилиндрические проекции. В этих проекциях параллели - это параллельные прямые, а меридианы - кривые или прямые, симметричные относительно среднего прямолинейного меридиана. Общие уравнения псевдоцилиндрических проекций выглядят так:
На рис. 3.9 приведен пример равновеликой псевдоцилиндрической проекции с меридианами в форме эллипсов. 3. Поперечно-цилиндрические. Для получения этих проекций вначале географические координаты переводятся в сферические полярные координаты, которые в свою очередь преобразуются с помощью некоторой обычной цилиндрической проекции. К этим проекциям относятся наиболее распространенные в мире проекции: проекции Гаусса-Крюгера и UTM. Общие уравнения поперечно-цилиндрических проекций выглядят следующим образом:
где X, Y - сферические полярные координаты поперечной системы, а r - константа. На рис. 3.10 приведены примеры наиболее распространенных в России поперечно-цилиндрических проекций.
Рис. 3.9. Равновеликая эллиптическая псевдоцилиндрическая проекция
(а) (б) Рис. 3.10. Поперечно-цилиндрическая проекция Гаусса-Крюгера для узкой (а) и широкой (б) полосы. Практически также как (а) выглядят проекции Кассини-Зольднера, Гаусса-Ламберта, а также Меркатора, которая известна также как UTM или проекция Гаусса-Боага
4. Конические проекции. В этих проекциях параллели - это концентрические окружности, а меридианы - пучок прямых, проведенных из центра окружностей. Общие уравнения конических проекций выглядят так:
где 5. Псевдоконические проекции. В этих проекциях параллели - это дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана, на котором расположен центр параллелей. Общие уравнения псевдоконических проекций выглядят так:
где q - полярное расстояние южной параллели на плоскости. Пример псевдоконической проекции приведены на рис. 3.12.
Рис. 3.11. Равноугольная коническая проекция с одинаковыми искажениями на крайних параллелях 10° и 80°
Рис. 3.12. Псевдоконическая проекция Штаба-Вернера (сердцевидная). Искажения отсутствуют на среднем меридиане (55°) и северном полюсе
6. Поликонические проекции. В этих проекциях параллели - это дуги эксцентрических окружностей с центрами, расположенными на среднем прямолинейном меридиане, а меридианы - кривые, симметричные относительно среднего меридиана и экватора.
Общие уравнения поликонических проекций выглядят так:
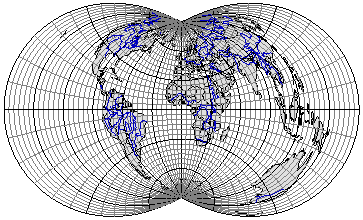
Вариант поликонической проекции приведен на рис. 3.13. 7. Азимутальные проекции. В этих проекциях параллели (альмукантараты) - это концентрические окружности, а меридианы (вертикалы) - прямые линии, пересекающиеся в центре окружностей под углами, равными разностям долгот соответствующих меридианов.
Рис. 3.13. Ортогональная поликоническая проекция
Общие уравнения азимутальных проекций выглядят так:
где z, a - сферические полярные координаты точек
Рис. 3.14. Равновеликая азимутальная проекция шара Ламберта. Аналогично выглядит проекция Постеля (в ней также отсутствуют искажения вдоль стандартной параллели)
8. Псевдоазимутальные проекции. Они применяются, когда нужно передать эффект сферичности Земли. В этих проекциях параллели - это концентрические окружности, а меридианы - кривые или прямые, сходящиеся в центре параллелей, при этом меридианы 0° и 360° совпадают. Общие уравнения псевдоазимутальных проекций выглядят так:
где z, a - сферические полярные координаты точек
(а) (б)
Рис. 3.15. Псевдоазимутальная проекция Гинзбурга (а - простая, б - с эффектом выпуклости)
(а) (б)
Рис. 3.16. Гномическая (а) и ортографическая (б) проекция (перспективно-азимутальная с негативным изображением) 9. Перспективные проекции (рис. 3.16). К этим проекциям относят проекции, в которых поверхность Земли отображается прямолинейными визирными лучами из точек пространства, называемыми точками зрения, на развертывающиеся поверхности цилиндра (при этом получается перспективно-цилиндрическая проекция), конуса (перспективно-коническая) или плоскость (перспективно-азимутальная - самая распространенная). 10. Проекции для карт глобусов. Глобусы обычно изготавливаются путем оклеивания шаровых заготовок или путем выдавливания пленки в полусферы. В первом способе (методе оклейки) вначале изготавливаются меридианные полосы с изображением размером в 30° по долготе и в 140° по широте, не включая полярные шапки за 70-ми параллелями. Для построения изображения на этих полосах обычно используется видоизмененная простая поликоническая проекция, сохраняющая длины на среднем меридиане, на всех параллелях и имеющая незначительные искажения на крайних меридианах. Формулы этих проекций для этих полос представляют в следующем виде:
где R - радиус референц-сферы,
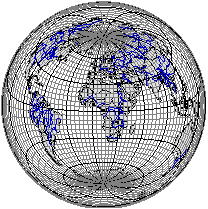
Рис. 3.17. Развертка глобуса Для построения изображений полярных шапок обычно применяется прямая равнопромежуточная вдоль меридианов азимутальная проекция рис. 3.17). Во втором способе (методе выдавливания) изображение наносится на специальную тонкую пленку, отличающуюся равномерностью вытяжки в продольном и поперечном направлении при выдавливании плоскости в полусферу. Выдавливание предварительно нагретой пленки производится с помощью специального пресса. Картографическое изображение, наносимое на пленку, строится в видоизменённой равнопромежуточной вдоль меридианов азимутальной проекции с учетом необходимых величин её растяжения при выдавливании. Формулы этих проекций имеют вид:
где R - радиус референц-сферы, а 10. Переменно-масштабные проекции. Такие проекции могут быть использованы для картографирования неравномерно распределенных в пространстве объектов и явлений, когда существует необходимость сжатия или растяжения отдельных участков земной поверхности. 11. Проекции анаморфированных изображений. В анаморфированных изображениях (анаморфизмах) величина масштаба в различных точках карты плавно меняется пропорционально значениям некоторого параметра (плотности некоторого явления), распределенного по всей карте. Целью анаморфического преобразования является выравнивание плотности по всей карте. Например, если в качестве выравнивающего параметра выбрать плотность населения, то наиболее плотно населенные районы увеличатся в размерах, а менее населенные - уменьшатся. Такие изображения называются эквидемическими (рис. 3.18).
Рис. 3.18. Эквидемическая карта мира (анаморфизм по населению отдельных регионов стран)
Среди всего множества проекций в России наиболее часто используется «двойная» равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера, сохраняющая длины на среднем меридиане. Эта проекция наиболее хорошо подходит для картографирования территории Российской Федерации, имеющий большой территориальный охват. Для топографических карт многих стран мира в настоящее время применяется проекция UTM - универсальная поперечно-цилиндрическая проекция Меркатора, называемая также проекцией Гаусса-Боага. Эта проекция отличается от проекции Гаусса-Крюгера только тем, что на среднем меридиане частный масштаб длин равен не единице, а 0,9996.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 809; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.88.120 (0.014 с.) |

 (рис. 3.1). Вместо коэффициента сжатия эллипсоиды иногда характеризуют эксцентриситетом
(рис. 3.1). Вместо коэффициента сжатия эллипсоиды иногда характеризуют эксцентриситетом  .
.


 ), начальный пункт в Пулково, превышение геоида над референц-эллипсоидом в начальном пункте равно нулю, а измерение высот делается в Балтийской системе высот, ведущей отсчет от нуля Кронштатского футштока. Эта система координат называется СК-42, т.к. она была разработана в 1942 г., а с 1946 г. была введена в эксплуатацию на территории СССР. Тем не менее, на Дальнем Востоке иногда используется другая система высот от уровня Охотского моря.
), начальный пункт в Пулково, превышение геоида над референц-эллипсоидом в начальном пункте равно нулю, а измерение высот делается в Балтийской системе высот, ведущей отсчет от нуля Кронштатского футштока. Эта система координат называется СК-42, т.к. она была разработана в 1942 г., а с 1946 г. была введена в эксплуатацию на территории СССР. Тем не менее, на Дальнем Востоке иногда используется другая система высот от уровня Охотского моря.


 .
.

 ). Это связано с тем, что в системе этого референц-эллипсоида выдают координаты приемники американской системы глобального позиционирования GPS, которая всё шире применяется в практике геодезических работ.
). Это связано с тем, что в системе этого референц-эллипсоида выдают координаты приемники американской системы глобального позиционирования GPS, которая всё шире применяется в практике геодезических работ.
 - координаты начала координат второй системы в первой, M - масштабный коэффициент,
- координаты начала координат второй системы в первой, M - масштабный коэффициент,  - разворот осей на малые углы.
- разворот осей на малые углы.
 и долготой
и долготой  , измеряемыми в градусах от экватора и от Гринвичского меридиана соответственно (рис. 3.4). Координаты любой точки в пространстве складываются из широты и долготы её проекции по нормали на эллипсоид и высоты H точки относительно эллипсоида. В связи с тем, что широта и долгота точки на местности зачастую определяется с помощью астрономических наблюдений, географические координаты также иногда называются астрономическими.
, измеряемыми в градусах от экватора и от Гринвичского меридиана соответственно (рис. 3.4). Координаты любой точки в пространстве складываются из широты и долготы её проекции по нормали на эллипсоид и высоты H точки относительно эллипсоида. В связи с тем, что широта и долгота точки на местности зачастую определяется с помощью астрономических наблюдений, географические координаты также иногда называются астрономическими. , задаваемой в географической системе координат (
, задаваемой в географической системе координат ( - это высота точки
- это высота точки  над уровнем референц-эллипсоида). Ось Z топоцентрической системы координат совпадает с нормалью к поверхности эллипсоида, проходящей через
над уровнем референц-эллипсоида). Ось Z топоцентрической системы координат совпадает с нормалью к поверхности эллипсоида, проходящей через  , ось X лежит в плоскости меридиана и направлена на северный полюс, а ось Y направлена на восток (рис. 3.5).
, ось X лежит в плоскости меридиана и направлена на северный полюс, а ось Y направлена на восток (рис. 3.5).




 и
и  получаются различные семейства проекций. Рассмотрим основные классы проекций.
получаются различные семейства проекций. Рассмотрим основные классы проекций.






 - полярный радиус южной параллели, а
- полярный радиус южной параллели, а  . На рис. 3.11 приведен пример равноугольной конической проекции.
. На рис. 3.11 приведен пример равноугольной конической проекции.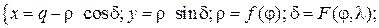




 . Вариант азимутальной проекций приведены на рис. 3.14.
. Вариант азимутальной проекций приведены на рис. 3.14.





 - длина дуги меридиана от экватора до данной параллели
- длина дуги меридиана от экватора до данной параллели 

 - константа, определяемая с учетом растяжения пленки.
- константа, определяемая с учетом растяжения пленки.



