
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналоговое и числовое кодирование. Единицы измерения объемов информации. Характерные объемы и информации и скорости их обработки. Информационная избыточность. Архивация и сжатие информации.Содержание книги
Поиск на нашем сайте Распределение Бернулли, Биномиальное распределение. Распределение Пуассона. Определение и свойства.
Распределение Бернулли, Биномиальное распределение. Распределение Пуассона. Определение и свойства. Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи. Определение Случайная величина
Принято говорить, что событие
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из Определение Пусть
имеет биномиальное распределение с параметрами
Случайную величину Функция вероятности задаётся формулой:
где
— биномиальный коэффициент. Функция распределения Функция распределения биномиального распределения может быть записана в виде суммы:
где
Моменты Производящая функция моментов биномиального распределения имеет вид:
откуда
а дисперсия случайной величины.
Свойства биномиального распределения
Связь с другими распределениями
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в теории массового обслуживания. Определение Выберем фиксированное число
где
Тот факт, что случайная величина Моменты Производящая функция моментов распределения Пуассона имеет вид:
откуда
Для факториальных моментов распределения справедлива общая формула:
где А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

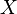 имеет распределение Бернулли, если она принимает всего два значения:
имеет распределение Бернулли, если она принимает всего два значения:  и
и  с вероятностями
с вероятностями  и
и  соответственно. Таким образом:
соответственно. Таким образом: ,
,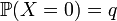 .
. соответствует «успеху», а событие
соответствует «успеху», а событие  — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
— «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.







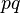

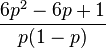

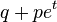

 независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна
независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна 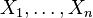 — конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром
— конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром 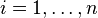 величина
величина  принимает значения
принимает значения  соответственно. Тогда случайная величина
соответственно. Тогда случайная величина
 .
. обычно интерпретируют как число успехов в серии из
обычно интерпретируют как число успехов в серии из 

 ,
, обозначает наибольшее целое, не превосходящее число
обозначает наибольшее целое, не превосходящее число 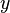 , или в виде неполной бета-функции:
, или в виде неполной бета-функции: .
. ,
, ,
, ,
,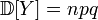 .
. и
и  . Тогда
. Тогда 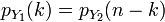 .
. и
и  . Тогда
. Тогда  .
. , то, очевидно, получаем распределение Бернулли.
, то, очевидно, получаем распределение Бернулли.  , где
, где  — нормальное распределение с математическим ожиданием
— нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией 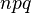 .
. — фиксированное число, то
— фиксированное число, то  , где
, где  — распределение Пуассона с параметром
— распределение Пуассона с параметром  и
и  соответственно, то условное распределение случайной величины
соответственно, то условное распределение случайной величины  – гипергеометрическое
– гипергеометрическое  .
.

 — число «испытаний»
— число «испытаний» 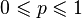 — вероятность «успеха»
— вероятность «успеха»









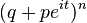
 и определим дискретное распределение, задаваемое следующей функцией вероятности:
и определим дискретное распределение, задаваемое следующей функцией вероятности: ,
, обозначает факториал числа
обозначает факториал числа 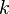 ,
, — основание натурального логарифма.
— основание натурального логарифма.  .
. ,
, ,
,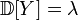 .
. ,
,



