

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Дискретные и непрерывные случайные величины. Функция распределения и плотность распределения. Критерии Колмогорова-Смирнова и Манна-Уитни. Классы «scale», «ordinal»и «nominal»случайных величин.
Содержание книги
- Принципы фон неймана построения архитектуры компьютеров. Поколения эвм.
- Вероятность и случайные величины
- История разработки показателя относительного риска
- Аналоговое и числовое кодирование. Единицы измерения объемов информации. Характерные объемы и информации и скорости их обработки. Информационная избыточность. Архивация и сжатие информации.
- На практике используется несколько подходов к определению объема выборки для получения статистически значимого результата.
- Интернет: возможности и технологии. Сетевые протоколы, web. Ip-адреса, url, html, теги, скрипты. Поисковые сервисы. Web 2. 0, блоги и социальные сети.
- О смысле ошибок первого и второго рода
- Вероятности ошибок (уровень значимости и мощность критерия.)
- Условия и ограничения применения критерия хи-квадрат Пирсона
- Дискретные и непрерывные случайные величины. Функция распределения и плотность распределения. Критерии Колмогорова-Смирнова и Манна-Уитни. Классы «scale», «ordinal»и «nominal»случайных величин.
- Процентиль — статистическая характеристика: среднее для каждого из интервалов в выборке, ранжированной на 100 интервалов.
- Распределения непрерывных случайных величин
- Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
- Оценки математического ожидания и дисперсии
- Предельные теоремы теории вероятностей.
- Интерфейсы. Определение интерфейса. Последовательные и параллельные интерфейсы. Внутренние и внешние интерфейсы современных персональных компьютеров.
- Расчет доверительных интервалов для процентилей.
- Построение доверительного интервала для коэффициента корреляции
- Оценка уровня силы корреляционной связи между несколькими случайными величинами. Корреляционная адаптометрия.
- Сила связи Направление связи
- Предположения линейной регрессии
- Физические и логические устройства. Драйверы. Файловая система.
- Назначение баз данных. Текстографические и фактографические базы данных. Реляционные базы данных. Транзакции, откаты транзакций.
- Демографические модели. Модель Мальтуса. Модель с взаимодействием по типу конкуренции за общий ресурс. Демографическая модель с дискретным временем.
- Демографическая модель с дискретным временем
- База данных Access. Поиск данных при помощи запросов. Логические операции, используемые в запросах
- Математические модели системы из двух взаимодействующих популяций
- Математические модели эпидемического процесса.
Похожие статьи вашей тематики
| Понятие случайной величины
| | | В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
|
|  . .
| (5.2)
| Далее рассматриваются отличия между дискретной и непрерывной случайными величинами.
| | Дискретная случайная величина. Закон распределения дискретной случайной величины
| | | Рассмотрим дискретную случайную величину на примере.
Пример 1.
Число появлений герба при трех бросаниях монеты является дискретной случайной величиной Х. Возможные значения числа появлений герба: 0,1,2,3. Следует найти вероятность появления герба в одном испытании.
Решение. Вероятность появления герба в одном испытании равна p=1/2.
Противоположное ему событие: герб не выпал, вероятность этого события по формуле (4.5) равна q=1-p=1/2.
1) Событие 1. «Три раза бросили монету и ни разу герб не выпал». Это сложное событие состоит из появления трёх совместных и независимых элементарных событий: «герб не выпал в одном испытании». Для события «три раза бросили и ни разу герб не выпал», которое обозначим Р(0), вероятность вычисляется по формуле умножения (4.7) для независимых событий:
 .
2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб выпал в одном из трёх совместных испытаний». Для события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле (4.2а), где каждое слагаемое вычисляется по формуле умножения (4.7) для независимых событий: .
2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб выпал в одном из трёх совместных испытаний». Для события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле (4.2а), где каждое слагаемое вычисляется по формуле умножения (4.7) для независимых событий:
 .
3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий: .
3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий:
 .
4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется по формуле умножения (4.7). .
4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется по формуле умножения (4.7).
 .
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях.
q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях.
Результаты вычислений вынесены в таблицу 5.1.
Таблица 5.1 .
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях.
q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях.
Результаты вычислений вынесены в таблицу 5.1.
Таблица 5.1
| Событие Х
| герб не выпал
| герб выпал 1 раз
| герб выпал 2 раза
| герб
выпал 3 раза
| | хi
|
|
|
|
| | Вероятность события:
Р(хi)= рi
| 
| 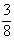
| 
| 
| Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:
1) таблично (рядом распределения);
2) графически;
3) аналитически (в виде формулы).
В примере 1 закон распределения задан в виде ряда распределения (таблицей 5.1), где представлены все возможные значения хi и соответствующие им вероятности рi = Р (Х = хi ). При этом вероятности рi удовлетворяют условию:
 , ,
потому что
 , ,
где число возможных значений n может быть конечным или бесконечным.
Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (хi) откладываются по оси абсцисс, а вероятности (рi) – по оси ординат. Точки Аi c координатами (хi, рi) соединяются ломаными линиями.
Функция F(х) для дискретной случайной величины вычисляется по формуле:
|
|  , ,
| (5.3)
| где суммирование ведется по всем значениям i, для которых хi< х.
Пример 2.
Для задачи в примере 1 найти функцию распределения вероятности F(х) этой случайной величины и построить ее. Построить многоугольник распределения.
Решение.
Если х £ 0, то F(х) = Р (Х < х) = 0.
Если 0 < х £ 1, то F(х) = Р (Х < х) = 1/8.
Если 1 < х £ 2, то F(х) = Р (Х < х) = 1/8 + 3/8 = 0,5.
Если 2 < х £ 3, то F(х) = Р (Х < х) = 1/8 + 3/8 + 3/8 = 7/8.
Если х > 3, то F(х) = Р (Х < х) = 1/8 + 3/8 + 3/8 + 1/8 = 1.
В таблицу 5.2 внесены значения функции распределения вероятности F(х) случайной величины – х.
Таблица 5.2
| №
|
|
|
|
|
| | хi
|
|
|
|
| >3
| | функция распределения F(х)
|
| 0,125
| 0,5
| 0,875
|
| Для построения многоугольника распределения значения случайной величины х переписаны в другой форме из таблицы 5.1 в таблицу 5.3.
Таблица 5.3
| №
|
|
|
|
| | хi
|
|
|
|
| | Ряд распределения Р(хi)= рi
| 0,125
| 0,375
| 0,375
| 0,125
|
Многоугольник распределения и полученная функция распределения вероятности представлены на рис. 5.1, 5.2.

Рис. 5.1. Многоугольник распределения

Рис. 5.2. Функция распределения
| | Числовые характеристики дискретных случайных величин
|
| | 1) Математическое ожидание М(Х) дискретной случайной величины Х это сумма произведений всех возможных значений величины Х на соответствующие вероятности:
|
| М(Х) = x1· p1 + x2· p2 + … + xn· pn.
| (5.4)
| Свойства математического ожидания:
- Математическое ожидание имеет ту же размерность, что и сама случайная величина.
- Математическое ожидание может быть как положительным, так и отрицательным числом.
- Математическое ожидание постоянной величины С равно этой постоянной. М (С) = С.
- Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.
М (X + Y +... + W) = М (X) + М (Y) +... + М (W).
- Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
М (XY) = M(X) × M(Y).
- Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С× М(Х).
2) Дисперсия D(X) дискретной случайной величины Х – это математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания:
|
| D(X) = M [X – M(X)]2.
| (5.5)
| Формула (5.5) после возведения в степень и преобразований имеет вид:
|
| D(X) = M (X2) – [M(X)]2.
| (5.6)
| Свойства дисперсии:
Дисперсия имеет размерность, равную квадрату размерности случайной величины.
Дисперсия постоянной величины всегда равна нулю: D (С) = 0.
Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D (СX) = С2×D(X).
Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией: D(X +Y) = D(X) + D(Y).
3) Среднее квадратическое отклонение s(Х) дискретной случайной величины Х определяется формулой (5.2). Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина.
Случайная величина называется центрированной, если математическое ожидание M(X)=0, и стандартизированной, если M(X)=0 и среднее квадратическое отклонение s = 1.
Рассмотрим на примере вычисление числовых характеристик дискретных случайных величин.
Пример 3.
Найти математическое ожидание М (Х), дисперсию D(Х) и среднее квадратическое отклонение s(Х) дискретной случайной величины Х, заданной законом распределения в таблице 5.4.
Таблица 5.4
Решение. Математическое ожидание Х вычисляется по формуле (5.4):
М(Х)= –5× 0,4 + 2× 0,3 + 3× 0,1 + 4× 0,2 = -0,3.
Дисперсия вычисляется по формуле (5.6): D(Х) = М(Х2) – [М(Х)]2.
Закон распределения квадрата Х2 случайной величины задан в таблице 5.5.
Таблица 5.5
Математическое ожидание Х2:
М(Х2) = 25×0,4 + 4×0,3 + 9× 0,1 + 16×0,2 = 15,3.
Искомая дисперсия:
D(Х) = М(Х2) – [М(Х)]2 = 15,3 – (– 0,3)2 = 15,21.
Тогда среднее квадратическое отклонение будет:  . .
| | Непрерывная случайная величина Функция распределения вероятностей и плотность распределения вероятностей непрерывной случайной величины
| | | Если рассматривать случайную величину Х, значения которой заполняют интервал (a,b) и составить перечень всех возможных её значений невозможно, то она называется непрерывной. В результате этого появилась необходимость дать общий способ задания любых типов случайных величин. Для этого вводится функция распределения вероятностей случайной величины. Функция распределения F(х) для непрерывной случайной величины имеет вид:
|
|  , ,
| (5.7)
| где: f(х) – функция плотности вероятности вычисляется по формуле:
|
|  . .
| (5.8)
| Функцию распределения F(х) называют интегральным законом распределения, плотность вероятности f(х). называют дифференциальным законом распределения.
Свойства функции распределения F(х):
Свойство 1. Значения функции распределения F(х) принадлежат отрезку [0, 1]:
0 £ F(х) £ 1.
Свойство 2. F(х) – неубывающая функция:
F (х1) £ F(х2 ), если х1< х2.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) равна приращению функции распределения на этом интервале:
Р (а £ Х <b) = F(b) – F(а).
Свойство 3.Если возможные значения случайной величины принадлежат интервалу (a,b), то:
F(x)=0 при x£a;
F(x)=1 при x³b.
Следствие 2. Если возможные значения непрерывной случайной величины расположены на всей оси х, то:
 ; ; 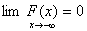 . .
Свойства плотности вероятности f(х):
Свойство 1. Плотность вероятности не может быть отрицательной: f(х) ³ 0.
Свойство 2.
|
|  . .
| (5
9)
| Следствие. В частности, если значения случайной величины находятся в интервале (a, b), то вероятность попадания в заданный интервал
|
|  . .
| (5.9а)
| Функция распределения связана с плотностью формулой:
|
|  . .
| | | Числовые характеристики непрерывной случайной величины
| | | | |
Математическое ожидание
Математическое ожидание непрерывной случайной величины Х:
|
|  . .
| (5.11)
| f(х) – плотность вероятности распределения случайной величины Х.
Дисперсия
Дисперсия непрерывной случайной величины Х:
|
| 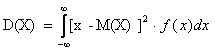 . .
| (5.12)
| |
|  . .
| (5.13)
|
|



 .
.
 .
2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб выпал в одном из трёх совместных испытаний». Для события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле (4.2а), где каждое слагаемое вычисляется по формуле умножения (4.7) для независимых событий:
.
2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб выпал в одном из трёх совместных испытаний». Для события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле (4.2а), где каждое слагаемое вычисляется по формуле умножения (4.7) для независимых событий:
 .
3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий:
.
3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий:
 .
4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется по формуле умножения (4.7).
.
4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется по формуле умножения (4.7).
 .
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях.
q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях.
Результаты вычислений вынесены в таблицу 5.1.
Таблица 5.1
.
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях.
q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях.
Результаты вычислений вынесены в таблицу 5.1.
Таблица 5.1

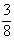


 ,
, ,
, ,
,


 .
. ,
,
 .
.
 ;
; 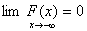 .
. .
.
 .
.
 .
.
 .
.
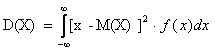 .
.
 .
.



