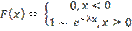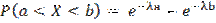Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція розподілу ймовірностей. Непереривні випадкові величини.Содержание книги
Поиск на нашем сайте
Щільність ймовірностей. Функцией распределения (вероятностей) СВ Х называют функцию F(x): F(x) = Р(Х<х). Функция распределения в точке х равна вероятности того, что СВ Х принимает значение меньше х. Свойства F(x) 1. Функция распределения СВ Х есть неотрицательная функция, заключенная между 0 и 1: 0 2. На минус бесконечности функция распределения = 0: F(- 3. На плюс бесконечности функция распределения =1: F(+ 4. Функция распределения есть неубывающая функция своего аргумента: F(x1) Непрерывная СВ – случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка; непрерывно занимает некоторый промежуток. Задается функцией распределения и функцией плотности. Плотностью распределения (плотностью вероятности или просто плотностью) непрерывной СВ называется производная ее функции распределения: 1. Плотность вероятности –неотрицательная функция: f(x) 2. Несобственный интеграл в бесконечных пределах от плотности вероятности НСВ равен 1: 3. Площадь под кривой распределения f(x) равна 1. Для любой СВ: Р(а<X<b)= F(b)-F(a). Для НСВ: P(a<X<b)= Для НСВ вводятся те же числовые характеристики, что и для ДСВ. В формулах для их вычисления суммы заменяются интегралами, например: М(Х) = причем, требуется, чтобы написанный несобственный интеграл сходился абсолютно. Для НСВ Х вводится еще одна характеристика – медиана Ме(Х) – следующим равенством: Р(Х < Me(X)) = P(X > Me(X)). Числові характеристики ВВ. Математичне сподівання та дисперсія. Моменти випадкових величин і їх властивості. Математическое ожидание СВ – это среднее значение СВ или точка на числовой оси, вокруг которой группируются все возможные значения СВ. Физический смысл - «центр тяжести», «центр масс» М(х) = М[х] = m Для ДСВ: m Свойства мат. ожидания: 1)Мат.ожидание постоянной величины равно самой постоянной величине М[С]=С 2)Постоянный множитель можно выносить за знак мат.ожидания: М[кХ] = к М[Х] 3)Мат.ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их мат.ожиданий: М[X+Y]= М[X] 4) Мат.ожидание произведения конечного числа независимых случайных величин равно произведению их мат.ожиданий: М[X 5)Если все значения СВ увеличить (уменьшить) на постоянную величину С, то на эту же постоянную величину С увеличится (уменьшится) и ее мат.ожидание: М[X 6)Мат.ожидание отклонения СВ от ее мат.ожидания равно 0: М[X- М(X)]= М[ Дисперсией СВ Х называется математическое ожидание квадрата ее отклонения от мат.ожидания. D(х) = D[х] = D Средним квадратическим отклонением или стандартным отклонением СВ Х называется арифметическое значение корня из ее дисперсии ДСВ: D Свойства дисперсии: 1.Дисперсия постоянной величины равна 0: D[C]=0 2. Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат D[kX]=k 3. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий: D[X+Y]= D[X] + D[Y] 4. Дисперсия СВ равна разности мат.ожидания квадрата СВ и квадрата ее мат.ожидания: D[X]= М[X Начальный момент к-го порядка – математическое ожидание к-ой степени этой величины: Центральный момент к-го порядка СВ Х – математическое ожидание к-ой степени отклонения СВ Х от ее мат.ожидания ДСВ: Мода (Пирсон, 1894) – наиболее часто встречающееся (самое модное) значение переменной. Например, модный цвет платья или песня на радио, т.е. это варианта, имеющая наибольшую частоту. Нормальний, рівномірний та показниковий (експоненціальний) закони Розподілу. Равномерное распределение - непрерывная величина, принимающая значение из некоторого интервала, ни одно из значений которого не является более вероятным. Функцией плотности распределения непрерывной случайной величины X называют функцию f (х)— первую производную от функции распределения F(х):
Функция распределения случайной величины Х, распределенная по равномерному закону на отрезке [a,b]
M[x] = Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл: Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a,b], то:
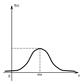
М (X) = m, т. е. математическое ожидание нормального распределения равно параметру m. Изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если m возрастает, и влево, если m убывает. С возрастанием σ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох; при убывании σ нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси Оу. Функция распределения нормального закона с параметрами N(m,σ) равна
Для нормального распределения матожидание равно моде и медиане Нормально распределенная с параметрами т и s случайная величина практически всегда принимает значения из промежутка (т – 3s; т + 3s).
Функция распределения плотности экспоненциального закона
Вероятность попадания случайной величины в интервал [a,b]:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

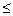 F(x)
F(x) 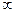 ) = lim F(x)=0.
) = lim F(x)=0.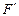 (x)=f(x) или F(x) =
(x)=f(x) или F(x) = 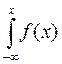
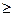 0
0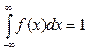
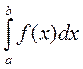 .
.

 Для НСВ: m
Для НСВ: m 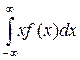
 М[Y]
М[Y] Y]= М[X]
Y]= М[X] 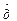 ]=0
]=0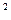 ], a= М[X]
], a= М[X]
 НСВ: D
НСВ: D 
 ДСВ:
ДСВ:  НСВ:
НСВ: 
 = М[x
= М[x  ] = М[(X-m
] = М[(X-m 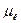 =
=  НСВ:
НСВ: 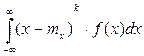
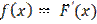
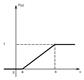
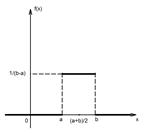 Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его:
Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его: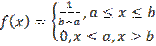 Кривая распределения равномерного закона R(a,b)
Кривая распределения равномерного закона R(a,b)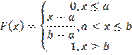
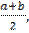 D[x] =
D[x] = 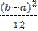 , Ass = 0, Ex = -1.2
, Ass = 0, Ex = -1.2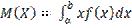
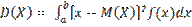 Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу [а, b], равна определенному интегралу от плотности распределения, взятому в пределах от а до b: P(a < X < b) =
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу [а, b], равна определенному интегралу от плотности распределения, взятому в пределах от а до b: P(a < X < b) = 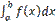
 Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью:
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью: 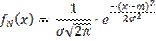
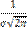 Нормальное распределение определяется двумя параметрами: m и σ.
Нормальное распределение определяется двумя параметрами: m и σ.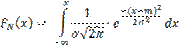
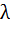
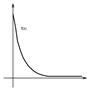 Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х,с параметром
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х,с параметром 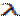 , которое описывается плотностью
, которое описывается плотностью 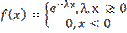
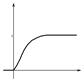 M(x) =
M(x) = 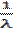 , Dx =
, Dx =