
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теореми додавання та множення ймовірностей.Содержание книги
Поиск на нашем сайте
Сумма событий А и В есть событие А+В, состоящее в наступлении хотя бы одного из событий А или В. Произведение событий А и В есть событие А*В, состоящее в совместном наступлении обоих событий А и В. События называются несовместными, если их совместное наступление невозможно.
Некоторые свойства: Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью Р(А/В). События А и В называются независимыми, если Р(А/В) = Р(А) (или Р(В/А) = Р(В)). Теорема умножения 1. (ТУ1): Р(АВ) = Р(А)*Р(В/А) = Р(В)*Р(А/В). ТУ 2.: вероятность совместного наступления независимых событий равна произведению их вероятностей. Теорема сложения 1. (ТС1): вероятность суммы попарно несовместных событий равна сумме их вероятностей.
ТС 3.: Р(А+В) = Р(А) + Р(В) – Р(АВ).
Формула повної ймовірності. Формула Байєса. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B1, B2,..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р (А) = Р (В1) PB1 (А) + Р (В2) PB2 (A) +... + Р(Вn)РBn(А). Эту формулу называют «формулой полной вероятности». Основные определения и формулы: Пусть событие А может произойти только совместно с одним из попарно несовместных событий Н1, Н2, …, Нn (это имеет место, например, для полной группы событий Нк, к = 1.. n). Тогда: Р(А) = Если при этом Р(А) ¹ 0, то Р(Нm/А) = Выбор подходящих гипотез Н1, Н2, …, Нn зависит от того, можем ли мы достаточно просто вычислить условные вероятности Р(А/Нк).
Послідовності випробувань. Повторюванні експерименти. Схема Бернуллі. Локальна і інтегральна теореми Муавра-Лапласа. Поліноміальна схема. Сформулируем основные формулы и определения, пусть осуществляется n независимых повторений некоторого эксперимента (или n независимых экспериментов), в каждом из которых может произойти событие А. Если вероятность этого события в каждом испытании равна р, то вероятность Р(n;k) того, что в n испытаниях событие А наступит ровно к раз определяется формулой Бернулли: Р(n;k) = В случае когда вероятность события А в m -ом испытании равна pm, m = 1.. n, вероятность Р(n;k) равна коэффициенту при zk в разложении производящей функции: G(z) = P(n;k1;k2;…;km) = Основные формулы и определения для большого N Пусть в каждом из независимых испытаний событие А может произойти с вероятностью q, q = 1 – p. Обозначим как и раньше, через P(n;k) вероятность ровно к появлений события А в n испытаниях. кроме того, пусть P(n; k1, k2) – вероятность того, что число появлений события А находится между к1и к2. Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то P(n;k) Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то P(n; k1, k2) Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций: а) j(-х) = j(х), F(-х) = -F(х); б) при больших х j(х)» 0, F(х)» 0,5. Теоремы Лапласа дают удовлетворительное приближение при npq ³ 9. Теорема Пуассона. Если n – велико, а р – мало, то P(n;k) Эта формула дает удовлетворительное приближение для р £ 0,1и np £ 10. При больших np рекомендуется применять формулы Лапласа. Випадкові величини (ВВ). Дискретні та неперервні ВВ. Случайная величина(СВ) – величина, которая в результате опыта может принять то или иное значение, неизвестно заранее – какое именно. Закон распределения СВ – всякое соотношение, устанавливающее связь между всевозможными значениями СВ и соответствующими вероятностями. Дискретная СВ – случайная величина, множество значений которой конечно или счетное и принимает отдельные, изолированные значения с определенными вероятностями. Задается рядом распределения, многоугольником распределения, функцией распределения. Ряд распределения – таблица, в которой перечислены возможные значения СВ Х и соответствующие им вероятности. Р Многоугольник распределения – Графическое изображение ряда распределения. Непрерывная СВ – случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка; непрерывно занимает некоторый промежуток. Задается функцией распределения и функцией плотности. Для НСВ вводятся те же числовые характеристики, что и для ДСВ. В формулах для их вычисления суммы заменяются интегралами, например: М(Х) = причем, требуется, чтобы написанный несобственный интеграл сходился абсолютно. Для НСВ Х вводится еще одна характеристика – медиана Ме(Х) – следующим равенством: Р(Х < Me(X)) = P(X > Me(X)). Распишем функцию от случайной величины. Пусть НСВ Х и Y связаны функциональной зависимостью Y = j(х), где j(х) – дифференцируемая функция, монотонная на всем интервале возможных значений СВ Х. Тогда, если f (x) – плотность СВ Х, а g(y) – плотность СВ Y, то g(y) = f(y(y))| y’(y)|, где y(y) – функция, обратная по отношению к j(х). Если на интервале возможных значений СВ Х обратная функция y(y) неоднозначна, т.е. одному значению у соответствует несколько значений х: y1(y), y2(y),…, yn(y), то плотность СВ Y определяется формулой:
Распишем функцию от 2-х случайных величин. Для функции нескольких случайных величин удобнее искать функцию распределения, а плотность определять дифференцированием. Если НСВ Z есть функция от двух случайных аргументов Х и Y: Z = j (X, Y), то ее функция распределения имеет вид:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.12.233 (0.006 с.) |


 Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
Противоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.
 ТС 2.: Р(А) = 1 – Р(А).
ТС 2.: Р(А) = 1 – Р(А).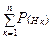 Р(А/Нк). (формула полной вероятности).
Р(А/Нк). (формула полной вероятности).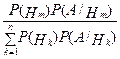 , m = 1.. n. (формула Байеса).
, m = 1.. n. (формула Байеса). .
. , где qm = 1 – рm. Другое обобщение формулы Бернулли состоит в следующем. Пусть в каждом из независимых испытаний может появиться одно из m несовместных событий Ai и P(Ai) = pi во всех испытаниях,
, где qm = 1 – рm. Другое обобщение формулы Бернулли состоит в следующем. Пусть в каждом из независимых испытаний может появиться одно из m несовместных событий Ai и P(Ai) = pi во всех испытаниях,  =1. Тогда вероятность Р(n;k1;k2;…;km) того, что в n испытаниях событие Ai произойдет ki раз, i = 1..m,
=1. Тогда вероятность Р(n;k1;k2;…;km) того, что в n испытаниях событие Ai произойдет ki раз, i = 1..m,  , определяется полиномиальной формулой:
, определяется полиномиальной формулой: .Наиболее вероятное число m0 появлений события А в n испытаниях (если в каждом испытании Р(А) = р) равно целой части числа р(n+1). Если р(n+1) – целое, то наибольшее значение вероятности Р(n;k) достигается при двух числах: m0 = р(n+1) и m0 = 1.
.Наиболее вероятное число m0 появлений события А в n испытаниях (если в каждом испытании Р(А) = р) равно целой части числа р(n+1). Если р(n+1) – целое, то наибольшее значение вероятности Р(n;k) достигается при двух числах: m0 = р(n+1) и m0 = 1. где
где  - функция Гаусса.
- функция Гаусса. где
где  - функция Лапласа.
- функция Лапласа. , где l = n*p.
, где l = n*p. = Р(Х=х
= Р(Х=х 


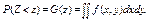 где f(x,y) – совместная плотность системы случайных величин (X, Y), а двойной интеграл берется по области D(Z) плоскости хОу, для которой j(x,y) < z.
где f(x,y) – совместная плотность системы случайных величин (X, Y), а двойной интеграл берется по области D(Z) плоскости хОу, для которой j(x,y) < z.


