
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральна сукупність, вибірка, основні способи організації вибірки. Емпірична функція розподілу. Полігони і гістограми.Содержание книги
Поиск на нашем сайте
Генеральная совокупность (ГС) – совокупность всех мыслимых и реально существующих наблюдений, произведенных при данном реальном комплексе условий. ГС – аналог СВ. ГС – все объекты, которые подлежат исследованию. Выборочная совокупность (ВС) или выборка – подмножество объектов ГС, непосредственно участвующих в исследовании. Объем генеральной совокупности – число объектов ГС. Объем выборочной совокупности – число объектов ВС. Репрезентативная (представительная) выборка – выборка, которая достаточно хорошо представляет пропорции ГС. Способы отбора выборки - Бесповторный отбор (схема невозвращенного шара) – каждый элемент, случайно отобранный из ГС, исследуется и не возвращается назад в ГС. - Повторный отбор (схема возвращенного шара) – каждый элемент, случайно отобранный из ГС, исследуется и возвращается назад в ГС. В качестве модели ГС выбирается выборочная совокупность неограниченного объема. Способы представления выборки - простой статистический ряд, - вариационный ряд, - частотно-вариационный ряд, - сгруппированный частотный ряд (интервальный или статический ряд) Графические способы изображения выборки
2. Гистограмма – это столбиковая диаграмма, эмпирический аналог функции плотностей распределения. По оси OX – интервальный ряд, по оси OY – величина i H:
Статистическая функция распределения в данной точке x равняется накопленной относительной частоте или статистической вероятности того, что CВ принимает значение меньше за x: По оси ОУ: относительные частоты накопленным порядком или накопленные статистические вероятности.
Статистичне оцінювання параметрів. Ґрунтовна, незміщена, ефективна Статистична оцінка. Інтервальні статистичні оцінки. Любое значение неизвестного искомого параметра генеральной совокупности, вычисленное на основе выборочных данных, носит элемент случайности. Такое случайное приближенное значение параметра генеральной совокупности называется оценкой параметра генеральной совокупности (или выборочным, статистическим параметром генеральной совокупности). Оценка параметра генеральной совокупности, полученная по выборке и выраженная одним числом, называется точечной. Произвольную оценку параметра а будем обозначать. a. Оценка параметра ГС называется “ доброкачественной”, если она удовлетворяет трем требованиям: - состоятельность; - несмещенность; - эффективность. 1. Оценка a* параметра а называется состоятельной, если она по вероятности при увеличении числа опытов сходится к оцениваемому параметру:
2. Оценка a* параметра а называется несмещенной, если ее матожидание равно оцениваемому параметру: M [a* n] = a 3. Несмещенная оценка a* параметра а называется эффективной, если она имеет минимальную дисперсию среди всех возможных несмещенных оценок параметра а, вычисленных по выборкам одного и того же объема n: D[a*n] → min. В качестве доброкачественных статистических оценок параметров генеральной совокупности необходимо иметь оценки, одновременно удовлетворяющие требованиям несмещенности, состоятельности, эффективности, такие оценки или близкие к ним обозначают: Оценка матожидания Точечная оценка матожидания по вариационному ряду – это среднеарифметическое наблюденных значений: Для других законов: В качестве оценки m по частотно-вариационному ряду принимают средневзвешенную оценку: где xi – вариант, k – количество вариантов в выборке. Для интервального ряда: х` i – середина i-го интервала, mi – количество элементов выборки, попавших в i -тый интервал, k – количество интервалов. Оценка дисперсии Оценка дисперсии для интервального ряда вычисляется по формуле: Выборочный коэффициент асимметрии по вариационному ряду находится по формуле: Выборочный коэффициент эксцесса для вариационного ряда находится по формуле:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.232.94 (0.006 с.) |

 1. Полигон (частот или частостей ) может быть построен по вариационному, частотно-вариационному или по интервальному ряду. По ОХ откладываются либо выборочные значения, либо варианты, либо интервалы. По ОУ – частота либо статистическая вероятность.
1. Полигон (частот или частостей ) может быть построен по вариационному, частотно-вариационному или по интервальному ряду. По ОХ откладываются либо выборочные значения, либо варианты, либо интервалы. По ОУ – частота либо статистическая вероятность.

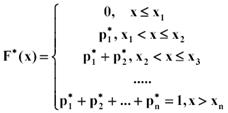 Статистической функцией распределения – называется функция:
Статистической функцией распределения – называется функция: 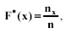 где nx - количество элементов в выборке, меньше чем x, n - объем выборки.
где nx - количество элементов в выборке, меньше чем x, n - объем выборки.


 Для нормального закона:
Для нормального закона:  .
. .
.

 и с учетом поправки на группировку Шеппарда:
и с учетом поправки на группировку Шеппарда: 





