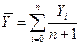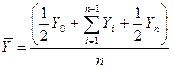Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распишем 2- мерную непрерывную случайную величину.Содержание книги
Поиск на нашем сайте Совместная функция распределения F(x, y) =P{(X < x)(Y < y)} 2-мерной СВ (X, Y), обладает следующими свойствами: 1. F(-¥, -¥) = F(-¥, y)=F(x, -¥)=0; F(+¥, +¥)=1; 2. F(x, +¥) = F1(x) – функция распределения СВ Х; 3. F(+¥, y) = F2(y) – функция распределения СВ Y. 4. F(x, y) – неубывающая функция по каждому из аргументов. В случае, если Х и Y непрерывные СВ, совместный закон распределения можно задавать совместной плотностью f(x,y) системы (Х, Y): Две СВ Х и Y называются независимыми если f1(x/y) = f1(x) или f2(y/х) = f2(y). Если Х и Y независимы, то совместная плотность системы (X, Y) равна произведению плотностей Х и Y: f(x,y) = f1(x)* f2(y). Корреляционным моментом двух СВ Х и Y называют величину: K=M(XY) – M(X)M(Y). Если Х и Y – непрерывны и f(x,y) – их совместная плотность, то: Коэффициентом корреляции двух СВ Х и Y называют безразмерную величину r:
Регрессионный анализ данных. Условное среднее Предсказанные значения зависимой переменной – значения Коэффициент детерминации и скорректированный коэффициент детерминации
Наибольшее применение получили уравнения регрессии, отражающие взаимосвязь одной зависимой переменной с одной (парная регрессия) или несколькими (множественная регрессия) независимыми переменными. Чаще всего используют следующие парные и множественные зависимости:
Обычно стараются использовать линейные зависимости или зависимости приводимые к линейным путем преобразования переменных. Параметры уравнения регрессии подбираются методом наименьших квадратов, который обеспечивает минимальную сумму квадратов отклонений фактических величин Y от вычисленных по уравнению регрессии для заданных значений независимых переменных. Для линейной регрессии парного типа В общем виде функция множественной регрессии имеет вид Регрессионный анализ данных предполагает, что выбирается наиболее оптимальный вид функции регрессии Часові ряди. Ряд динамики, или временной ряд – последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Каждое конкретное значение называется уровнем ряда. Интервальный динамический ряд характеризуется последовательностью, когда уровни ряда относятся к результату, накопленному или произведенному за определенный интервал времени (ряды объемов продукции по месяцам года, объемы перевозок за недели, месяцы или кварталы, экономические показатели предприятий по отдельным периодам и т.д.). Моментный динамический ряд характеризуется последовательностью, когда уровни ряда показывают фактическое наличие изучаемого явления на конкретный момент времени (ряды численности населения на начало года, величины запасов сырья на начало периода и т.д.). Комплексные ряды - отображают динамику совокупности нескольких разных показателей во времени. Цели анализа временных рядов направлены на определение природы ряда или его прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Показатели, исчисляемые как отношение уровня ряда в данный момент или интервал времени к непосредственно предшествующему уровню, называются цепными, т.е. цепные коэффициенты (темпы) роста равны Абсолютный прирост – разность двух уровней ряда динамики. Цепной абсолютный прирост исчисляется как разность между сравниваемым уровнем Темп прироста – это абсолютный прирост в относительных величинах. Цепной темп прироста представляет собой отношение сравниваемого цепного абсолютного прироста Средний уровень ряда – показатель, обобщающий итоги развития явления за определенный интервал из имеющейся временной последовательности. Для интервальных временных рядов с равными периодами времени средний уровень равен:
Для моментных временных рядов при условии, что в пределах каждого периода развитие происходило по линейному закону, средний уровень (среднее хронологическое) равен: Многие монотонные временные ряды можно хорошо приблизить линейной функцией. Если же имеется явная монотонная нелинейная компонента, то данные вначале следует преобразовать, чтобы устранить нелинейность. Обычно для этого используют логарифмическое, экспоненциальное или (менее часто) полиномиальное преобразование данных.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

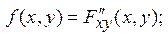

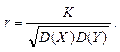
 - среднее арифметическое наблюдавшихся значений величины Y, соответствующих X=x. Функция изменения условного среднего
- среднее арифметическое наблюдавшихся значений величины Y, соответствующих X=x. Функция изменения условного среднего  от независимой переменной X называется уравнением регрессии. Уравнения регрессии строятся для зависимых переменных. Эти переменные входят в левую часть уравнения. Независимые переменные входят в правую часть уравнения и позволяют предсказывать зависимую переменную.
от независимой переменной X называется уравнением регрессии. Уравнения регрессии строятся для зависимых переменных. Эти переменные входят в левую часть уравнения. Независимые переменные входят в правую часть уравнения и позволяют предсказывать зависимую переменную. , вычисленные по уравнению регрессии с оцененными коэффициентами регрессии. Остатки – разности между наблюдаемыми и предсказанными значениями зависимой переменной:
, вычисленные по уравнению регрессии с оцененными коэффициентами регрессии. Остатки – разности между наблюдаемыми и предсказанными значениями зависимой переменной: 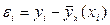 . Сумма квадратов остатков - сумма вида
. Сумма квадратов остатков - сумма вида 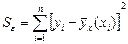 Сумма квадратов зависимой переменной, скорректированная на среднее
Сумма квадратов зависимой переменной, скорректированная на среднее 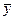
 Сумма квадратов предсказанной зависимой переменной, скорректированная на среднее
Сумма квадратов предсказанной зависимой переменной, скорректированная на среднее  Известно, что для суммы квадратов указанных величин, выполняется равенство:
Известно, что для суммы квадратов указанных величин, выполняется равенство: 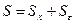 .
.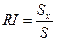 ,
,  , где
, где  - число наблюдений,
- число наблюдений,  - число параметров модели (число независимых переменных плюс 1, так как обычно в модель включается свободный член).
- число параметров модели (число независимых переменных плюс 1, так как обычно в модель включается свободный член). ;
; 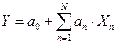 (парная и множественная линейная регрессия);
(парная и множественная линейная регрессия);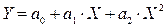 ;
; 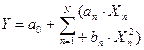 (парная и множественная параболич. р.);
(парная и множественная параболич. р.); ;
;  (парная и множественная гиперболич. регрессия);
(парная и множественная гиперболич. регрессия); ;
;  (парная и множественная степенная регрессия)
(парная и множественная степенная регрессия) ;
;  ;
;  (парная и множествен. показательн р.)
(парная и множествен. показательн р.)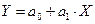 коэффициенты
коэффициенты  и
и  находятся из решения системы уравнений:
находятся из решения системы уравнений: 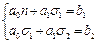 =>
=> 
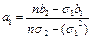
 , где
, где  - функция остатков с нулевым средним и неизвестной дисперсией, определяющая случайное отклонение зависимой переменной от уравнения регрессии. Предполагается, что величины
- функция остатков с нулевым средним и неизвестной дисперсией, определяющая случайное отклонение зависимой переменной от уравнения регрессии. Предполагается, что величины  из набора (1)-(5), оцениваются коэффициенты функции регрессии
из набора (1)-(5), оцениваются коэффициенты функции регрессии 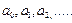 и строятся для них доверительные интервалы, проверяется гипотеза о значимости регрессии, оценивается степень адекватности модели и т.д.
и строятся для них доверительные интервалы, проверяется гипотеза о значимости регрессии, оценивается степень адекватности модели и т.д.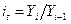 . Если же для сравнения взят общий уровень, то такие показатели называются базисными, т.е. базисные коэффициенты (темпы) роста равны
. Если же для сравнения взят общий уровень, то такие показатели называются базисными, т.е. базисные коэффициенты (темпы) роста равны 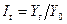 . Здесь
. Здесь 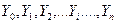 - последовательность абсолютных уровней ряда.
- последовательность абсолютных уровней ряда.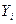 и уровнем, который предшествует ему, т.е.
и уровнем, который предшествует ему, т.е. 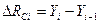 . Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем
. Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем 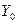 , т.е.
, т.е. 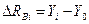 .
.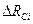 к предшествующему уровню
к предшествующему уровню 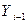 , т.е.
, т.е. 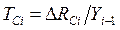 . Базисный темп прироста - отношение сравниваемого базисного абсолютного прироста
. Базисный темп прироста - отношение сравниваемого базисного абсолютного прироста 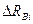 к уровню, принятому за постоянную базу
к уровню, принятому за постоянную базу 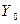 , т.е.
, т.е.  .
.