

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Интернет: возможности и технологии. Сетевые протоколы, web. Ip-адреса, url, html, теги, скрипты. Поисковые сервисы. Web 2. 0, блоги и социальные сети.
Содержание книги
- Принципы фон неймана построения архитектуры компьютеров. Поколения эвм.
- Вероятность и случайные величины
- История разработки показателя относительного риска
- Аналоговое и числовое кодирование. Единицы измерения объемов информации. Характерные объемы и информации и скорости их обработки. Информационная избыточность. Архивация и сжатие информации.
- На практике используется несколько подходов к определению объема выборки для получения статистически значимого результата.
- Интернет: возможности и технологии. Сетевые протоколы, web. Ip-адреса, url, html, теги, скрипты. Поисковые сервисы. Web 2. 0, блоги и социальные сети.
- О смысле ошибок первого и второго рода
- Вероятности ошибок (уровень значимости и мощность критерия.)
- Условия и ограничения применения критерия хи-квадрат Пирсона
- Дискретные и непрерывные случайные величины. Функция распределения и плотность распределения. Критерии Колмогорова-Смирнова и Манна-Уитни. Классы «scale», «ordinal»и «nominal»случайных величин.
- Процентиль — статистическая характеристика: среднее для каждого из интервалов в выборке, ранжированной на 100 интервалов.
- Распределения непрерывных случайных величин
- Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
- Оценки математического ожидания и дисперсии
- Предельные теоремы теории вероятностей.
- Интерфейсы. Определение интерфейса. Последовательные и параллельные интерфейсы. Внутренние и внешние интерфейсы современных персональных компьютеров.
- Расчет доверительных интервалов для процентилей.
- Построение доверительного интервала для коэффициента корреляции
- Оценка уровня силы корреляционной связи между несколькими случайными величинами. Корреляционная адаптометрия.
- Сила связи Направление связи
- Предположения линейной регрессии
- Физические и логические устройства. Драйверы. Файловая система.
- Назначение баз данных. Текстографические и фактографические базы данных. Реляционные базы данных. Транзакции, откаты транзакций.
- Демографические модели. Модель Мальтуса. Модель с взаимодействием по типу конкуренции за общий ресурс. Демографическая модель с дискретным временем.
- Демографическая модель с дискретным временем
- База данных Access. Поиск данных при помощи запросов. Логические операции, используемые в запросах
- Математические модели системы из двух взаимодействующих популяций
- Математические модели эпидемического процесса.
Проверка статистических гипотез. Ошибки первого и второго рода. Доверительная вероятность и уровень статистической значимости р. Точные и асимптотические критерии.
Проверка статистических гипотез. Ошибки первого и второго рода. Доверительная вероятность и уровень статистической значимости р. Точные и асимптотические критерии.
Проверка статистических гипотез является содержанием одного из обширных классов задач математической статистики
Статистическая гипотеза — предположение о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть применением статистических методов к данным выборки
Определения
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина 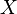 , распределение которой , распределение которой  полностью или частично неизвестно. Тогда любое утверждение, относительно полностью или частично неизвестно. Тогда любое утверждение, относительно  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них: называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
- Статистическая гипотеза, однозначно определяющая распределение
 , то есть , то есть  , где , где  какой-то конкретный закон, называется простой. какой-то конкретный закон, называется простой. - Статистическая гипотеза, утверждающая принадлежность распределения
 к некоторому семейству распределений, то есть вида к некоторому семейству распределений, то есть вида  , где , где 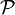 — семейство распределений, называется сложной. — семейство распределений, называется сложной. На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу  . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей или альтернативной. , называемая конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на случайной выборке  фиксированного объема фиксированного объема  для распределения для распределения  . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной. . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной.
Этапы проверки статистических гипотез
Формулировка основной гипотезы  и конкурирующей гипотезы и конкурирующей гипотезы  . .
- Задание уровня значимости
 , на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода. , на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода. - Расчёт статистики
 критерия такой, что: критерия такой, что: - её величина зависит от исходной выборки
 ; ; - по её значению можно делать выводы об истинности гипотезы
 ; ; - статистика
 , как функция случайной величины , как функция случайной величины  , также является случайной величиной и подчиняться какому-то закону распределения. , также является случайной величиной и подчиняться какому-то закону распределения. - Построение критической области. Из области значений
 выделяется подмножество выделяется подмножество  таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство  . Это множество . Это множество  и называется критической областью. и называется критической областью. - Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику
 и по попаданию (или непопаданию) в критическую область и по попаданию (или непопаданию) в критическую область  выносится решение об отвержении (или принятии) выдвинутой гипотезы выносится решение об отвержении (или принятии) выдвинутой гипотезы  . .
Виды критической области
Выделяют три вида критических областей:
- Двусторонняя критическая область определяется двумя интервалами
 , где , где  находят из условий находят из условий  . . - Левосторонняя критическая область определяется интервалом
 , где , где  находят из условия находят из условия  . . - Правосторонняя критическая область определяется интервалом
 , где , где 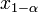 находят из условия находят из условия  . .
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Определения
Пусть дана выборка  из неизвестного совместного распределения из неизвестного совместного распределения  , и поставлена бинарная задача проверки статистических гипотез: , и поставлена бинарная задача проверки статистических гипотез:

где  — нулевая гипотеза, а — нулевая гипотеза, а  — альтернативная гипотеза. Предположим, что задан статистический критерий — альтернативная гипотеза. Предположим, что задан статистический критерий
 , ,
сопоставляющий каждой реализации выборки  одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации: одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
- Распределение
 выборки выборки  соответствует гипотезе соответствует гипотезе  , и она точно определена статистическим критерием, то есть , и она точно определена статистическим критерием, то есть  . . - Распределение
 выборки выборки  соответствует гипотезе соответствует гипотезе  , но она неверно отвергнута статистическим критерием, то есть , но она неверно отвергнута статистическим критерием, то есть 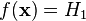 . . - Распределение
 выборки выборки  соответствует гипотезе соответствует гипотезе  , и она точно определена статистическим критерием, то есть , и она точно определена статистическим критерием, то есть 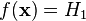 . . - Распределение
 выборки выборки  соответствует гипотезе соответствует гипотезе  , но она неверно отвергнута статистическим критерием, то есть , но она неверно отвергнута статистическим критерием, то есть  . . Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.
| | Верная гипотеза
| 
| 
| | Результат применения критерия
| 
|  верно принята верно принята
|  неверно принята (Ошибка второго рода) неверно принята (Ошибка второго рода)
| 
|  неверно отвергнута (Ошибка первого рода) неверно отвергнута (Ошибка первого рода)
|  верно отвергнута верно отвергнута
|
|



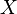 , распределение которой
, распределение которой  полностью или частично неизвестно. Тогда любое утверждение, относительно
полностью или частично неизвестно. Тогда любое утверждение, относительно  называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них: , где
, где  какой-то конкретный закон, называется простой.
какой-то конкретный закон, называется простой.  , где
, где 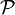 — семейство распределений, называется сложной.
— семейство распределений, называется сложной.  . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза
. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза  , называемая конкурирующей или альтернативной.
, называемая конкурирующей или альтернативной. фиксированного объема
фиксированного объема  для распределения
для распределения  , на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.  критерия такой, что:
критерия такой, что:  ;
; , также является случайной величиной и подчиняться какому-то закону распределения.
, также является случайной величиной и подчиняться какому-то закону распределения.  таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство  . Это множество
. Это множество  , где
, где  находят из условий
находят из условий  .
. , где
, где  находят из условия
находят из условия  .
. , где
, где 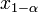 находят из условия
находят из условия  .
. из неизвестного совместного распределения
из неизвестного совместного распределения  , и поставлена бинарная задача проверки статистических гипотез:
, и поставлена бинарная задача проверки статистических гипотез:
 ,
, одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации: .
.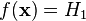 .
.


