Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы корреляционного анализаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Статистическая зависимость случайных величин. Уравнения регрессии Зависимость между значениями одной случайной величины и условным математическим ожиданием другой случайной величины носит название статистической. Чтобы изучить статистическую зависимость, нужно знать условное математическое ожидание случайной величины. Для его оценки необходимо знать аналитический вид двумерного распределения (X,Y). Однако, суждение об аналитическом виде двумерного распределения, сделанного по отдельной ограниченной по объёму выборке, может привести к серьёзным ошибкам. Поэтому идут на упрощение и переходят от условного математического ожидания случайной величины к условному среднему значению, т.е. принимают, что Статистическую зависимость Y от X описывают с помощью уравнения вида
где Обратную статистическую зависимость можно описать уравнением регрессии X на Y:
где Функции В зависимости от вида уравнений регрессии и формы соответствующих линий регрессии говорят о различной форме статистической зависимости между изучаемыми величинами – линейной, квадратичной, показательной и т.д. Если функции
где A,B,C,D – некоторые параметры, то описываемые этими уравнениями зависимости Y от X и X от Y называются линейными; линии регрессии при этом – прямые. Если линия регрессии не является прямой, то такую зависимость называют нелинейной. Как уже было сказано выше, возможности практического применения статистической зависимости Если функции
где Угловые коэффициенты
где Из курса аналитической геометрии следует, что коэффициент линейной регрессии (угловой коэффициент линии регрессии) численно равен тангенсу угла наклона линии регрессии к соответствующей оси координат. Следовательно, чем больше, например, коэффициент Корреляционная зависимость. Коэффициент корреляции Зависимость между значениями одной случайной величины и условным средним значением другой случайной величины носит название корреляционной (от англ. correlation – согласование, связь, взаимосвязь, соотношение, взаимозависимость); термин впервые введен Гальтоном в 1888г. Направление корреляционной связи – прямая; – oбратная. Сила корреляционной связи Схема оценки корреляционной связи по коэффициенту корреляции
Коэффициент корреляции Пирсона (1896 г.) изменяется в пределах от –1 до +1. Значение 0,00 интерпретируется как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Задачами корреляционного анализа являются: 1. Установить силу корреляционной связи. 2. Установить вид корреляционной связи (прямая или обратная).
Типовые задачи
Дан интервальный ряд величин X и Y, где X – длина волоса, Y – настриг шерсти овец.
Найти коэффициент регрессии; уравнение регрессии; коэффициент корреляции; коэффициент детерминации. Построить график зависимости настрига шерсти от длины волоса и график уравнения регрессии. Решение 1. Составим Табл. 4 и будем вносить в нее данные по мере выполнения необходимых расчетов (выполним округление до второго знака после запятой). Табл. 4
2. Среднюю арифметическую для длины волоса и настрига шерсти найдем по формулам:
Средняя длина волоса и настриг шерсти составляет 17,91 см и 4,63 кг соответственно. Дисперсия для длины волоса и настрига шерсти равна:
Среднее квадратическое отклонение для длины волоса и настрига шерсти равно:
Коэффициент вариации для длины волоса и настрига шерсти:
Среднее квадратическое отклонение показывает, что длина волос и настриг шерсти овец по данной совокупности колеблется в пределах 3. Найдем линейное уравнение регрессии. При парной корреляции устанавливают зависимость между двумя признаками, один из которых является факторным, другой - результативным. Связь между ними может иметь различный характер. Поэтому важно правильно установить форму связи между признаками и в соответствии с этим подобрать математическое уравнение, выражающее эту связь. После того, как определен вид уравнения связи, необходимо найти числовые значения его параметров. При вычислении параметров применяют различные методы: метод наименьших квадратов, метод средних, метод наименьшего предельного уклонения и др. Наиболее распространенным является метод наименьших квадратов. При его использовании находят такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических данных от расчетных является минимальной:
где y – фактическое значение результативного признака;
Построим график («корреляционное облачко») зависимости настрига шерсти (результативный признак) от длины волоса (факторный признак) (Рис. 9).
Рис. 9. Зависимость настрига шерсти от длины волоса Анализ исходных данных показывает, что с увеличением длины волоса настриг шерсти повышается (что подтверждается графиком). Расположение точек на графике показывает, что связь между признаками имеет прямолинейный характер и поэтому может быть выражена уравнением прямой линии:
Для определения неизвестных параметров уравнения а 0 и а 1 необходимо решить систему уравнений:
По данным таблицы 4 составим систему:
Из решения данной системы получим: ao = 3,072 a1 = 0,087 Тогда уравнение регрессии будет иметь вид: y = 0,087 x + 3,072 Коэффициент регрессии а 1 = 0,087 характеризует изменение настрига шерсти по данной совокупности в зависимости от длины волоса. При увеличении или уменьшении длины волоса на 1 ед. длины настриг шерсти овец, соответственно, увеличивается или уменьшается на 0,087 кг. 4. Построим линейное уравнение регрессии (Рис. 10).
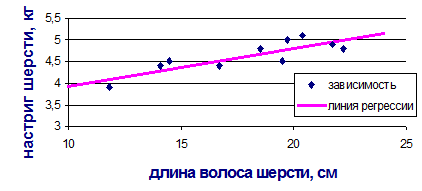
Рис. 10. Зависимость настрига шерсти от длины волоса. Уравнение регрессии Анализ графика показывает, что исходные данные лежат достаточно близко к прямой уравнения регрессии. Следовательно, выборка 10 овец из всего стада для проведения статистического анализа данных взята верно. 5. Коэффициент корреляции показывает не только тесноту связи, но и ее направление, меняется в пределах от −1 до +1.
где
Если коэффициент корреляции положительный, то связь между признаками прямая (прямо пропорциональная), если отрицательный, то связь обратная (обратно пропорциональная). Если коэффициент корреляции равен
Коэффициент детерминации равен квадрату коэффициента корреляции (r 2) и показывают, какая доля общей вариации результативного признака определяется изучаемым фактором.
Значение коэффициента корреляции близко к единице, следовательно, полученное уравнение регрессии достаточно хорошо описывает исследуемую зависимость. Коэффициент детерминации показывает, что 67% в среднегодовом настриге шерсти овец объясняется длиной волоса. Остальные 33% – неучтенные факторы (толщина волоса, грязь и т.д.). Вопросы для самопроверки
1. В чем состоит различие между функциональной и статистической зависимостью между случайными величинами? 2. В чем состоят две основные задачи корреляционного анализа? 3. Какую корреляционную зависимость называют линейной? 4. Запишите выборочные уравнения прямых регрессии. Дайте определение выборочного коэффициента корреляции и перечислите его основные свойства. 5. Что следует сказать о зависимости двух случайных величин, если коэффициент корреляции равен нулю? Если коэффициент корреляции ранен единице? Если коэффициент корреляции ранен минус единице? 6. В чем суть метода наименьших квадратов для определения параметров линии регрессии?
Варианты контрольной работы При выполнении и оформлении контрольной работы студент должен придерживаться следующих правил: 1. В заголовке контрольной работы должны быть ясно выписаны фамилия студента, его инициалы, номер задания. 2. Контрольную работу следует выполнять в тетради, обязательно чернилами (не красными), с оставлением полей для замечаний преподавателя. 3. Решения контрольных задач и задач для самостоятельного изучения следует располагать в порядке номеров, указанных в заданиях; перед решением каждой задачи надо выписывать полностью ее условие. 4. Графики следует выполнять с использованием карандаша и линейки. 5. В графическом изображении необходимо отразить название графика и подписи по осям. 6. В работе следует записывать полное решение. Контрольная работа, выполненная небрежно, без промежуточных вычислений, с пропуском задач и без соблюдения изложенных выше правил, возвращается обратно для переработки. Контрольная работа, выполненная не по своему варианту, не проверяется. Номер варианта соответствует последней цифре номера студенческого билета (зачетной книжки). Задание 1 Дан статистический ряд нормально распределенной случайной величины х. Рассчитать среднее арифметическое, среднее квадратическое, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Построить полигон распределения, гистограмму и кумуляту. Вариант 1
хi – температура животного. Вариант 2
хi –длина яиц Вариант 3
хi – масса тушек бройлера. Вариант 4
хi – масса 3-х месячных телят. Вариант 5
хi – масса тушек бройлера. Вариант 6
хi – масса 3-х месячных телят. Вариант 7
хi – масса тушек кролика. Вариант 8
хi – масса тушек индейки. Вариант 9
хi – масса печени. Вариант 10
хi – масса легкого животного
Задание 2 Вычислить коэффициент корреляции, коэффициент детерминации, найти уравнение регрессии двух случайных величин Х и У. Построить график зависимости величин Х и У и уравнения прямой регрессии.
Библиографический список 1. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М.: Юрайт-Издат; серия: Бакалавр. Базовый курс, 2013. – 479 с. 2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие / В.Е. Гмурман. – М.: Юрайт Издат; серия: Бакалавр. Прикладной курс, 2014. – 418 с. 3. Федькина, Т.В. Использование математических методов в животноводстве и ветеринарии: учеб.-метод. пособие / Т.В.Федькина. – М.: ФГОУ ВПО МГАВМиБ им. К. И. Скрябина, 2010. – 93 с. 4. Джугели, Т.П. Статистическая обработка экспериментальных данных: Метод. указ. / Т.П.Джугели, И.В.Кутликова, Т.В.Федькина. – М.: ФГОУ ВПО МГАВМиБ, 2008. – 54 с.
Содержание
Введение. 3 1 Статистическое распределение и числовые характеристики выборки. 4 1.1 Выборки и их характеристики. 4 1.1.1 Выборочный метод и способы составления выборок. 4 1.1.2 Статистическое распределение и его геометрическое изображение. 5 1.1.3 Числовые характеристики вариационного ряда. 6 1.2 Статистические оценки. 11 1.2.1 Точечные оценки. 11 1.2.2 Интервальные оценки. 13 1.2.3 Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии. 13 1.2.4 Доверительный интервал для оценки математического ожидания при неизвестной дисперсии. 15 1.2.5 Доверительный интервал для оценки среднего квадратического отклонения нормального распределения. 16 1.3 Типовые задачи. 17 1.4 Вопросы для самопроверки. 24 2 Элементы корреляционного анализа. 25 2.1 Статистическая зависимость случайных величин. Уравнения регрессии. 25 2.2 Корреляционная зависимость. Коэффициент корреляции. 26 2.3 Типовые задачи. 27 2.4 Вопросы для самопроверки. 31 3 Варианты контрольной работы.. 32 Библиографический список. 35
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

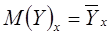

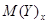 – условное математическое ожидание величины Y, соответствующее данному значению х. х – отдельные значения величины Х;
– условное математическое ожидание величины Y, соответствующее данному значению х. х – отдельные значения величины Х;  – некоторая функция. Это уравнение называется уравнением регрессии Y на Х.
– некоторая функция. Это уравнение называется уравнением регрессии Y на Х.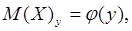
 - условное математическое ожидание величины Х, соответствующее данному значению y случайной величины Y;
- условное математическое ожидание величины Х, соответствующее данному значению y случайной величины Y;  - некоторая функция.
- некоторая функция.
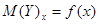 весьма ограниченны. Поэтому для характеристики формы связи между двумя случайными величинами, полученными в результате выборочных наблюдений, используют корреляционную зависимость
весьма ограниченны. Поэтому для характеристики формы связи между двумя случайными величинами, полученными в результате выборочных наблюдений, используют корреляционную зависимость  (или
(или 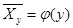 ). Уравнения, описываемые подобной зависимостью, называют выборочными уравнениями регрессии.
). Уравнения, описываемые подобной зависимостью, называют выборочными уравнениями регрессии.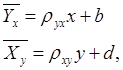
 и
и  – условные средние значения величин Y и X, параметры b и d – оценки B и D,
– условные средние значения величин Y и X, параметры b и d – оценки B и D,  и
и  – выборочные оценки коэффициентов A и C.
– выборочные оценки коэффициентов A и C. ;
; 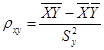 ,
,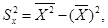
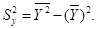
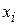
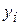
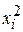

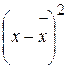
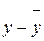
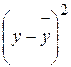
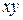
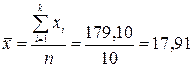
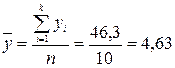
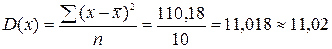



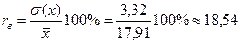

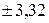 см и
см и 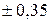 кг. соответственно. Коэффициент вариации составляет 18,54% для длины волоса 7,56% для настрига шерсти. Следовательно, разброс величин по длине волоса средний, а по настригу незначительный.
кг. соответственно. Коэффициент вариации составляет 18,54% для длины волоса 7,56% для настрига шерсти. Следовательно, разброс величин по длине волоса средний, а по настригу незначительный.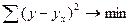 ,
,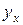 - расчетное значение результативного признака.
- расчетное значение результативного признака.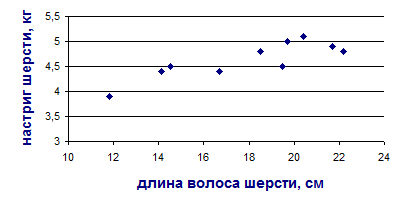
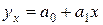

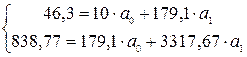
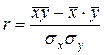 ,
,
 - средние значения факторного и результативного признаков;
- средние значения факторного и результативного признаков;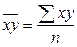 - среднее значение произведений факторного и результативного признаков;
- среднее значение произведений факторного и результативного признаков;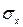 ,
, 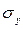 - средние квадратические отклонения факторного и результативного признаков.
- средние квадратические отклонения факторного и результативного признаков.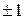 , то имеет место линейная зависимость между признаками. Если коэффициент корреляции равен нулю, то линейной зависимости между признаками нет.
, то имеет место линейная зависимость между признаками. Если коэффициент корреляции равен нулю, то линейной зависимости между признаками нет.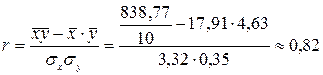 .
.