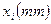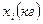Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гордеева Ю.Л., Левченкова Т.В.Содержание книги Поиск на нашем сайте
Гордеева Ю.Л., Левченкова Т.В. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ДАННЫХ Методические указания и контрольные задания для самостоятельной работы
Москва 2015 УДК 311.2(07) Кишкинова, О.А., Кутликова И.В., Гордеева Ю.Л., Левченкова Т.В. Статистическое оценивание данных: учеб.-метод. указ. / О.А. Кишкинова, И.В. Кутликова, Ю.Л. Гордеева, Левченкова Т.В.– М.: ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина, 2015. – 36 с. В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задачи для самостоятельного решения контрольной работы и самостоятельного изучения материала, вопросы для самоподготовки по разделу математики «Элементы математической статистики».
Рекомендовано для студентов, обучающихся по направлениям: 36.03.01 «Ветеринарно-санитарная экспертиза», 36.05.01.«Ветеринария», 36.03.02 «Зоотехния». Рецензенты: профессор кафедры Радиобиологии и вирусологии им. академиков А.Д.Белова и В.Н. Сюрина ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина Е.И. Ярыгина.
Утверждено на заседании учебно-методической комиссии ветеринарно–биологического факультета ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина (протокол № 1 от 04.09.2015 г). Введение
Целью данных методических указаний является помощь студентам, изучающим теорию элементов математической статистики, в усвоении необходимых теоретических знаний и приобретении практических навыков для решения задач, квалифицированного использования статистической информации в целях принятия правильных решений в вопросах прогнозирования. Раздел «Элементы математической статистики» является одним из фундаментальных разделов математики, изучение которого способствует формированию общекультурных и профессиональных компетенций выпускника в соответствии с требованиями ФГОС ВПО к уровню подготовленности по направлениям 36.03.01 «Ветеринарно-санитарная экспертиза», 36.03.02 «Зоотехния» и ФГОС ВО по направлению 36.05.01.«Ветеринария». Знания, полученные при изучении раздела «Статистическое оценивание данных» являются базовыми для освоения раздела «Математическая статистика». В настоящих методических рекомендациях представлен материал по разделам: статистическое распределение и числовые характеристики выборки, элементы корреляционного анализа. По каждой теме приведены типовые задачи с решениями, вопросы и задачи для самопроверки, а также варианты контрольной работы по разделу «Элементы математической статистики». Статистическое распределение и числовые характеристики выборки Выборки и их характеристики Выборочный метод и способы составления выборок Математическая статистика – это наука, занимающаяся разработкой методов сбора, регистрации и обработки результатов наблюдений (измерений) с целью познания закономерностей случайных явлений массового характера. Совокупность предметов или явлений, имеющих какие-либо общие свойства как качественные, так и количественные, называется объектом наблюдения. Статистические данные – это числовая информация о том, какие значения принимают единицы измерения. Задачами математической статистики в зависимости от поставленной цели являются: 1. Приближенное определение закона распределения случайной величины. 2. Вычисление параметров распределения. 3. Оценка достоверности параметров распределения и правдоподобие гипотез распределения. Вся исследуемая совокупность однородных объектов называется генеральной совокупностью. Выборочная совокупность – это часть элементов генеральной совокупности, отобранных случайным образом с целью исследования. Объём совокупности (генеральной или выборочной) – это число входящих в неё объектов n. Выборочный метод статистики заключается в том, что в результате исследования объектов выборки делают заключение о генеральной совокупности. Объясняется это тем, что для генеральной совокупности исследование может быть: – трудоемким с большими затратами средств; – практически не осуществимым; – неограниченным во времени; – частично разрушающим или уничтожающим все объекты наблюдения. Существуют два основных способа составления выборки: 1.Повторный, когда один и тот же объект может попасть под наблюдение более одного раза. 2.Бесповторный, когда каждый выбранный объект не возвращается в генеральную совокупность. Первый способ можно рассматривать как независимые испытания, а второй – как зависимые.
Статистические оценки Одной из центральных задач математической статистики является задача оценивания теоретического распределения случайной величины на основе выборочных данных. При этом часто предполагается, что вид закона распределения генеральной совокупности известен, но неизвестны параметры этого распределения, такие как математическое ожидание, дисперсия. Требуется найти приближенные значения этих параметров, то есть получить статистические оценки указанных параметров. Определение. Статистической оценкой Рассматривая выборочные значения Если для оценки Если число наблюдений невелико, то замена неизвестного параметра
Точечные оценки
Статистические оценки могут быть точечными и интервальными. Точечные оценки представляют собой число или точку на числовой оси. Чтобы оценка Определение. Оценка
Поясним смысл этого равенства. Пусть Свойство состоятельности нужно проверять в первую очередь. Оно обязательно для любого правила оценивания. Несостоятельные оценки не используются. Определение. Оценка Это свойство оценки желательно, но не обязательно. Часто полученная оценка бывает смещенной, но ее можно поправить так, чтобы она стала несмещенной. Иногда, оценка бывает асимптотически несмещенной, то есть Требования несмещенности особенно важно при малом числе опытов. Определение. Несмещенная оценка Можно показать, что:
(при больших n разница между
относительная частота эмпирическая функция распределения выборки Для нахождения оценок неизвестных параметров используют различные методы. Наиболее распространенными являются: метод моментов, метод максимального правдоподобия (ММП), метод наименьших квадратов (МНК). Интервальные оценки При выборке малого объема точечная оценка может существенно отличаться от оцениваемого параметра. В этом случае целесообразно использовать интервальные оценки. Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Пусть найденная по данным выборки величина Поскольку Определение. Доверительной вероятностью (надежностью) оценки Обычно задается надежность Неравенство Определение. Доверительным интервалом называется интервал
Типовые задачи Дан статистический ряд нормально распределенной случайной величины Х, где х – масса тушек бройлера.
Найти: среднее арифметическое; среднее квадратическое; моду; медиану; размах вариации; дисперсию; среднее квадратическое отклонение; коэффициент вариации. Построить полигон распределения, гистограмму и кумуляту. Решение xi – конкретное значение признака X. fi – число единиц (частоты) совокупности с данным значением признака(частот). 1. Для нахождения числовых характеристик необходимо ранжировать ряд (по возрастанию). Ранжируем ряд: 0,9 0,9 0,9 1,2 1,2 1,2 1,4 1,4 1,4 1,4 1,4 1,5 1,5 1,6 1,6 1,6 1,6 1,6 1,6 1,6 1,7 1,7 1,7 1,7 1,7 1,8 1,8 1,8 1,8 1,8 1,8 2,0 2. Составим Табл.1 и будем вносить в неё данные по мере выполнения необходимых расчетов (выполним округление до второго знака после запятой). Табл. 1
Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности – частоты вариант f. Общая сумма частот вариационного ряда равна объему данной совокупности
где k – число групп; n – общее число наблюдений, или объем совокупности. 3. Необходимо определить вариацию средней массы тушек бройлера по всей совокупности. Вариация массы тушек бройлера определяется с помощью средней арифметической. Получим:
Средняя масса тушек бройлера составляет 1,52 кг. 4. Для измерения вариации применяют различные показатели, из которых основными являются размах вариации (лимит), среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Размах вариации определяется как разница между наибольшим и наименьшим значениями признака.
где xmin, xmax- минимальное и максимальное значение признака. Получим: R = 2,0 – 0,9 = 1,1 xmin = 0,9 xmax = 2,0 Среднее линейное отклонение - средняя арифметическая из абсолютных отклонений отдельных вариант от средней арифметической: Простая дисперсия
Взвешенная дисперсия
Получим:
Среднее квадратическое отклонение находится как квадратный корень из дисперсии. Показывает отклонение от среднего. Вопросы для самопроверки 1. Что понимается под генеральной совокупностью? 2. Что такое выборка, объем выборки? Как обеспечивается представительность выборки? 3. Как получают повторную и бесповторную выборки? 4. Перечислите способы отбора статистического материала. 5. Что такое частота появления варианты в выборке? 6. Как получают относительную частоту варианты в выборке? 7. Как получают вариационный ряд распределения? 8. Как графически изображают вариационные ряды? 9. Как построить многоугольник распределения относительных частот? 10. Как построить гистограмму распределения плотностей относительных частот? 11. Дайте определение моды и медианы выборки. 12. В чем сущность задачи по определению параметров генеральной совокупности? В чем особенность этой задачи? 13. Как вычисляется средняя арифметическая выборки при малых и больших ее объемах? 14. Как вычисляется дисперсия выборки в случаях малого и большого ее объемов? 15. Какую величину принимают за среднюю генеральной совокупности? 16. Какую величину принимают за дисперсию генеральной совокупности? 17. Что понимают под доверительным интервалом и доверительной вероятностью? 18. Как вычисляют среднее квадратическое отклонение выборки? 19. Какова вероятность попадания генеральной средней в интервал размером ±2 (±3) средних квадратических отклонения средней выборки при нормальном распределении? 20. Если доверительная вероятность будет увеличена, то как изменится доверительный интервал при других равных условиях? 21. Что надо сделать с объемом выборки, чтобы уменьшить доверительный интервал при том же значении доверительной вероятности? Сила корреляционной связи Схема оценки корреляционной связи по коэффициенту корреляции
Коэффициент корреляции Пирсона (1896 г.) изменяется в пределах от –1 до +1. Значение 0,00 интерпретируется как отсутствие корреляции. Корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Задачами корреляционного анализа являются: 1. Установить силу корреляционной связи. 2. Установить вид корреляционной связи (прямая или обратная).
Типовые задачи
Дан интервальный ряд величин X и Y, где X – длина волоса, Y – настриг шерсти овец.
Найти коэффициент регрессии; уравнение регрессии; коэффициент корреляции; коэффициент детерминации. Построить график зависимости настрига шерсти от длины волоса и график уравнения регрессии. Решение 1. Составим Табл. 4 и будем вносить в нее данные по мере выполнения необходимых расчетов (выполним округление до второго знака после запятой). Табл. 4
2. Среднюю арифметическую для длины волоса и настрига шерсти найдем по формулам:
Средняя длина волоса и настриг шерсти составляет 17,91 см и 4,63 кг соответственно. Дисперсия для длины волоса и настрига шерсти равна:
Среднее квадратическое отклонение для длины волоса и настрига шерсти равно:
Коэффициент вариации для длины волоса и настрига шерсти:
Среднее квадратическое отклонение показывает, что длина волос и настриг шерсти овец по данной совокупности колеблется в пределах 3. Найдем линейное уравнение регрессии. При парной корреляции устанавливают зависимость между двумя признаками, один из которых является факторным, другой - результативным. Связь между ними может иметь различный характер. Поэтому важно правильно установить форму связи между признаками и в соответствии с этим подобрать математическое уравнение, выражающее эту связь. После того, как определен вид уравнения связи, необходимо найти числовые значения его параметров. При вычислении параметров применяют различные методы: метод наименьших квадратов, метод средних, метод наименьшего предельного уклонения и др. Наиболее распространенным является метод наименьших квадратов. При его использовании находят такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических данных от расчетных является минимальной:
где y – фактическое значение результативного признака;
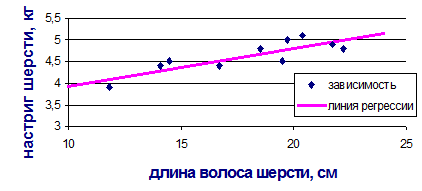
Построим график («корреляционное облачко») зависимости настрига шерсти (результативный признак) от длины волоса (факторный признак) (Рис. 9).
Рис. 9. Зависимость настрига шерсти от длины волоса Анализ исходных данных показывает, что с увеличением длины волоса настриг шерсти повышается (что подтверждается графиком). Расположение точек на графике показывает, что связь между признаками имеет прямолинейный характер и поэтому может быть выражена уравнением прямой линии:
Для определения неизвестных параметров уравнения а 0 и а 1 необходимо решить систему уравнений:
По данным таблицы 4 составим систему:
Из решения данной системы получим: ao = 3,072 a1 = 0,087 Тогда уравнение регрессии будет иметь вид: y = 0,087 x + 3,072 Коэффициент регрессии а 1 = 0,087 характеризует изменение настрига шерсти по данной совокупности в зависимости от длины волоса. При увеличении или уменьшении длины волоса на 1 ед. длины настриг шерсти овец, соответственно, увеличивается или уменьшается на 0,087 кг. 4. Построим линейное уравнение регрессии (Рис. 10).
Рис. 10. Зависимость настрига шерсти от длины волоса. Уравнение регрессии Анализ графика показывает, что исходные данные лежат достаточно близко к прямой уравнения регрессии. Следовательно, выборка 10 овец из всего стада для проведения статистического анализа данных взята верно. 5. Коэффициент корреляции показывает не только тесноту связи, но и ее направление, меняется в пределах от −1 до +1.
где
Если коэффициент корреляции положительный, то связь между признаками прямая (прямо пропорциональная), если отрицательный, то связь обратная (обратно пропорциональная). Если коэффициент корреляции равен
Коэффициент детерминации равен квадрату коэффициента корреляции (r 2) и показывают, какая доля общей вариации результативного признака определяется изучаемым фактором.
Значение коэффициента корреляции близко к единице, следовательно, полученное уравнение регрессии достаточно хорошо описывает исследуемую зависимость. Коэффициент детерминации показывает, что 67% в среднегодовом настриге шерсти овец объясняется длиной волоса. Остальные 33% – неучтенные факторы (толщина волоса, грязь и т.д.). Вопросы для самопроверки
1. В чем состоит различие между функциональной и статистической зависимостью между случайными величинами? 2. В чем состоят две основные задачи корреляционного анализа? 3. Какую корреляционную зависимость называют линейной? 4. Запишите выборочные уравнения прямых регрессии. Дайте определение выборочного коэффициента корреляции и перечислите его основные свойства. 5. Что следует сказать о зависимости двух случайных величин, если коэффициент корреляции равен нулю? Если коэффициент корреляции ранен единице? Если коэффициент корреляции ранен минус единице? 6. В чем суть метода наименьших квадратов для определения параметров линии регрессии?
Варианты контрольной работы При выполнении и оформлении контрольной работы студент должен придерживаться следующих правил: 1. В заголовке контрольной работы должны быть ясно выписаны фамилия студента, его инициалы, номер задания. 2. Контрольную работу следует выполнять в тетради, обязательно чернилами (не красными), с оставлением полей для замечаний преподавателя. 3. Решения контрольных задач и задач для самостоятельного изучения следует располагать в порядке номеров, указанных в заданиях; перед решением каждой задачи надо выписывать полностью ее условие. 4. Графики следует выполнять с использованием карандаша и линейки. 5. В графическом изображении необходимо отразить название графика и подписи по осям. 6. В работе следует записывать полное решение. Контрольная работа, выполненная небрежно, без промежуточных вычислений, с пропуском задач и без соблюдения изложенных выше правил, возвращается обратно для переработки. Контрольная работа, выполненная не по своему варианту, не проверяется. Номер варианта соответствует последней цифре номера студенческого билета (зачетной книжки). Задание 1 Дан статистический ряд нормально распределенной случайной величины х. Рассчитать среднее арифметическое, среднее квадратическое, моду, медиану, размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Построить полигон распределения, гистограмму и кумуляту. Вариант 1
хi – температура животного. Вариант 2
хi –длина яиц Вариант 3
хi – масса тушек бройлера. Вариант 4
хi – масса 3-х месячных телят. Вариант 5
хi – масса тушек бройлера. Вариант 6
хi – масса 3-х месячных телят. Вариант 7
хi – масса тушек кролика. Вариант 8
хi – масса тушек индейки. Вариант 9
хi – масса печени. Вариант 10
хi – масса легкого животного
Задание 2 Вычислить коэффициент корреляции, коэффициент детерминации, найти уравнение регрессии двух случайных величин Х и У. Построить график зависимости величин Х и У и уравнения прямой регрессии.
Библиографический список 1. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М.: Юрайт-Издат; серия: Бакалавр. Базовый курс, 2013. – 479 с. 2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие / В.Е. Гмурман. – М.: Юрайт Издат; серия: Бакалавр. Прикладной курс, 2014. – 418 с. 3. Федькина, Т.В. Использование математических методов в животноводстве и ветеринарии: учеб.-метод. пособие / Т.В.Федькина. – М.: ФГОУ ВПО МГАВМиБ им. К. И. Скрябина, 2010. – 93 с. 4. Джугели, Т.П. Статистическая обработка экспериментальных данных: Метод. указ. / Т.П.Джугели, И.В.Кутликова, Т.В.Федькина. – М.: ФГОУ ВПО МГАВМиБ, 2008. – 54 с.
Содержание
Введение. 3 1 Статистическое распределение и числовые характеристики выборки. 4 1.1 Выборки и их характеристики. 4 1.1.1 Выборочный метод и способы составления выборок. 4 1.1.2 Статистическое распределение и его геометрическое изображение. 5 1.1.3 Числовые характеристики вариационного ряда. 6 1.2 Статистические оценки. 11 1.2.1 Точечные оценки. 11 1.2.2 Интервальные оценки. 13 1.2.3 Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии. 13 1.2.4 Доверительный интервал для оценки математического ожидания при неизвестной дисперсии. 15 1.2.5 Доверительный интервал для оценки среднего квадратического отклонения нормального распределения. 16 1.3 Типовые задачи. 17 1.4 Вопросы для самопроверки. 24 2 Элементы корреляционного анализа. 25 2.1 Статистическая зависимость случайных величин. Уравнения регрессии. 25 2.2 Корреляционная зависимость. Коэффициент корреляции. 26 2.3 Типовые задачи. 27 2.4 Вопросы для самопроверки. 31 3 Варианты контрольной работы.. 32 Библиографический список. 35
Гордеева Ю.Л., Левченкова Т.В. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ДАННЫХ Методические указания и контрольные задания для самостоятельной работы
Москва 2015 УДК 311.2(07) Кишкинова, О.А., Кутликова И.В., Гордеева Ю.Л., Левченкова Т.В. Статистическое оценивание данных: учеб.-метод. указ. / О.А. Кишкинова, И.В. Кутликова, Ю.Л. Гордеева, Левченкова Т.В.– М.: ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина, 2015. – 36 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

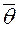 параметра
параметра  теоретического распределения называют его приближенное значение, зависящее от данных выбора.
теоретического распределения называют его приближенное значение, зависящее от данных выбора. как реализации случайных величин
как реализации случайных величин 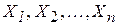 , получивших конкретные значения в результате опытов, можно представить оценку
, получивших конкретные значения в результате опытов, можно представить оценку 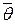 как функцию этих случайных величин:
как функцию этих случайных величин: 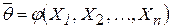 . Это означает, что оценка тоже является случайной величиной.
. Это означает, что оценка тоже является случайной величиной. взять несколько (k) выборок, то получим столько же случайных оценок
взять несколько (k) выборок, то получим столько же случайных оценок 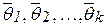 .
. :
: .
.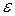 - очень малое положительное число. Тогда данное равенство означает, что чем больше объем выборки n, тем ближе оценка
- очень малое положительное число. Тогда данное равенство означает, что чем больше объем выборки n, тем ближе оценка  , то есть математическое ожидание оценки равно оцениваемому параметру. Если
, то есть математическое ожидание оценки равно оцениваемому параметру. Если 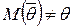 , то оценка
, то оценка 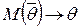 .
.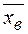 является состоятельной, несмещенной и эффективной оценкой
является состоятельной, несмещенной и эффективной оценкой 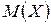 в классе линейных оценок;
в классе линейных оценок; является состоятельной, смещенной оценкой
является состоятельной, смещенной оценкой 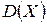 ;
;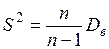 является состоятельной, несмещенной оценкой
является состоятельной, несмещенной оценкой 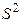 и
и 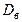 мала);
мала);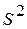 используется при малых выборках (обычно при n £30);
используется при малых выборках (обычно при n £30); появления события
появления события  в
в 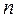 независимых испытаниях является состоятельной, несмещенной и эффективной оценкой, в классе линейных оценок, неизвестной вероятности
независимых испытаниях является состоятельной, несмещенной и эффективной оценкой, в классе линейных оценок, неизвестной вероятности  (p - вероятность появления события A в каждом испытании);
(p - вероятность появления события A в каждом испытании);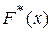 является состоятельной, несмещенной оценкой функции распределения
является состоятельной, несмещенной оценкой функции распределения  случайной величины X.
случайной величины X.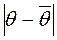 , то есть чем меньше
, то есть чем меньше  в неравенстве
в неравенстве 
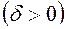 .
.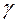 , с которой выполняется неравенство
, с которой выполняется неравенство 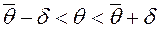 .
.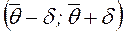 , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью 
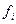

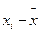
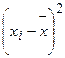

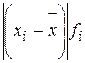
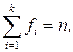
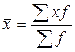 =
= 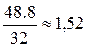
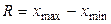

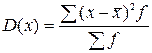

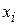
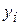
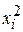

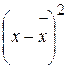
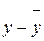
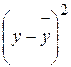
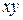
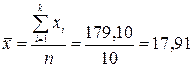
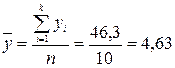
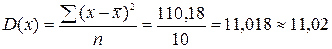



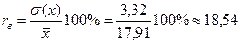

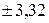 см и
см и 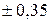 кг. соответственно. Коэффициент вариации составляет 18,54% для длины волоса 7,56% для настрига шерсти. Следовательно, разброс величин по длине волоса средний, а по настригу незначительный.
кг. соответственно. Коэффициент вариации составляет 18,54% для длины волоса 7,56% для настрига шерсти. Следовательно, разброс величин по длине волоса средний, а по настригу незначительный.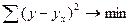 ,
, - расчетное значение результативного признака.
- расчетное значение результативного признака.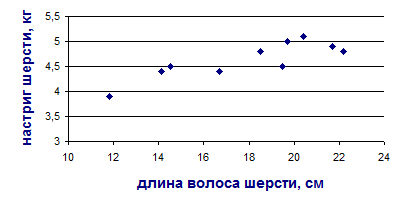
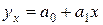

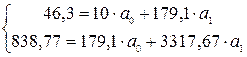
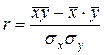 ,
,
 - средние значения факторного и результативного признаков;
- средние значения факторного и результативного признаков;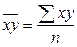 - среднее значение произведений факторного и результативного признаков;
- среднее значение произведений факторного и результативного признаков;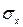 ,
, 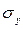 - средние квадратические отклонения факторного и результативного признаков.
- средние квадратические отклонения факторного и результативного признаков.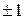 , то имеет место линейная зависимость между признаками. Если коэффициент корреляции равен нулю, то линейной зависимости между признаками нет.
, то имеет место линейная зависимость между признаками. Если коэффициент корреляции равен нулю, то линейной зависимости между признаками нет.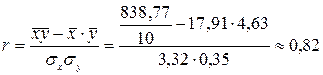 .
.