
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент детерминации этоСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте - квадрат парного коэффициента корреляции, - квадрат частного коэффициента корреляции, - квадрат среднего квадратического отклонения, - квадрат множественного коэффициента корреляции.
3. Факторная дисперсия вычисляется по формуле: -
- - -
4. Коэффициент детерминации показывает: - на сколько единиц изменится зависимая переменная, если независимая переменная изменится на 1 единицу; - на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%; - на сколько процентов изменение зависимой переменной зависит от изменения независимой переменной; долю вариации независимой переменной, обусловленную вариацией независимой переменной. Соу 2. Для оценки коэффициентов структурной формы модели не применяют метод наименьших квадратов...
- косвенный - - трехшаговый - обычный - двухшаговый Душутина Временные ряды 3. Построение модели временного ряда может быть осуществлено с использованием...:
- критерия Дарбина–Уотсона - метода последовательных разностей - мультипликативной модели - аддитивной модели Множественная регрессия Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой - коэффициент детерминации, - парный коэффициент корреляции, - частный коэффициент корреляции, - множественный коэффициент корреляции. 5.Величина, рассчитанная по формуле - коэффициента детерминации, - парного коэффициента корреляции, - частного коэффициента корреляции, - множественного коэффициента корреляции.
5.Дисперсионный анализ уравнения парной регрессии проверяет: - значимость коэффициента корреляции; - значимость уравнения регрессии; - значимость коэффициента регрессии; - значимость свободного члена уравнения регрессии. 6. Что минимизируется согласно методу наименьших квадратов:
Соу 3. Идентификация модели – это:
- единственность соответствия между приведенной и структурной формами модели - преобладание эндогенных переменных над экзогенными - преобладание экзогенных переменных над эндогенными Желтова Временные ряды 4. При моделировании временных рядов экономических показателей необходимо учитывать характер уровней исследуемых показателей... - Конструктивный - - независящий от времени - стохастический - аналитический Тест Чоу проводится для выяснения - автокорреляции остатков временного ряда - наличия гетероскедастичности в выборке - структурной стабильности тенденции временного ряда стационарности временного ряда Множественная регрессия Отметьте основные виды ошибок спецификации - отбрасывание значимой переменной, - добавление незначимой переменной, - низкое значение коэффициента детерминации, - выбор неправильной формы модели.
7. Дана ковариационная матрица вектора оценок коэффициентов регрессии:
Чему равна несмещенная оценка дисперсии элемента - 0,306; - 0,004; - 0,152; - -0,028. 8. Дана ковариационная матрица вектора оценок коэффициентов регрессии:
Чему равна несмещенная оценка дисперсии элемента - 0,306; - 0,004; - 0,152; - -0,028.
Соу 4. Модель идентифицируема, если: - число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели - число приведенных коэффициентов меньше числа структурных коэффициентов - число приведенных коэффициентов больше числа структурных коэффициентов Живаева Временные ряды 5. Если в модели присутствуют лаговые переменные, то это: - линейная модель; - нелинейная модель; - модель со случайными возмущениями; - динамическая модель. Множественная регрессия 7.На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше…., то считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включить только один из показателей xj или xe. Вставьте недостающее значение. - 0,3; - -0,6; - 0,8; - 0. 8.Оценить значимость парного линейного коэффициента корреляции можно при помощи: - критерия Фишера; - коэффициента автокорреляции; - критерия Стьюдента; - критерия Дарбина-Уотсона.
9.В линейной регрессии Y=b0+b1X+e параметрами уравнения регрессии являются:
- b0; - Y; - X; - b1 . 10.Величина коэффициента эластичности показывает …
- во сколько раз изменится в среднем результат при изменении фактора в два раза; - на сколько процентов изменится в среднем результат при изменении фактора на 1%; - предельно допустимое изменение варьируемого признака;
- предельно возможное значение результата. Соу 5. Модель неидентифицируема, если: - число коэффициентов структурной модели равно числу коэффициентов приведенной формы модели - число приведенных коэффициентов меньше числа структурных коэффициентов - число приведенных коэффициентов больше числа структурных коэффициентов Козичева Временные ряды 6. Установить соответствие:
- 1-Б, 2-Г, 3-В, 4-А - 1-А, 2-В, 3-Б, 4-Г - 1-В, 2-А, 3-Г, 4-Б - 1-Г, 2-Б, 3-А, 4-В Множественная регрессия 10.Частный критерий Фишера вычисляется по формуле:
- - - -
11.Уравнение множественной регрессии в стандартизованном виде имеет вид: - Сила влияния фактора х2 на результативный признак выше силы влияния фактора х1; - Сила влияния фактора х1 на результативный признак выше силы влияния фактора х2; - Сила влияния фактора х2 на результативный признак равна силе влияния фактора х1.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.141.142 (0.008 с.) |

 ;
; ;
;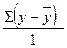 ;
; .
. является оценкой
является оценкой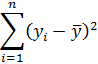
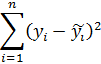
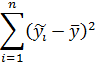
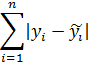
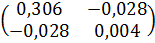
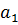 :
: :
: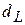 и верхним -
и верхним - 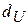 значениями критической точки
значениями критической точки

 или
или
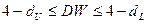
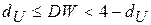
 ≤
≤ 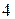
 ;
;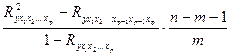 ;
;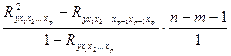 ;
;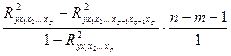 . Это прав ответ
. Это прав ответ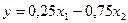 . Сила влияния какого фактора выше на результативный признак?
. Сила влияния какого фактора выше на результативный признак?


