
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы и их следствияСодержание книги
Поиск на нашем сайте
Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Для n несовместных событий теорема имеет вид:
Следствие 1. Сумма вероятностей несовместных событий, образующих полную группу событий, равна 1. Следствие 2. Сумма вероятностей противоположных событий равна 1:
Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
События называются независимыми, если появление одного из них не изменяет вероятности появления другого события. Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух или нескольких независимых событий равна произведению вероятностей этих событий:
Теорема умножения вероятностей зависимых событий. Вероятность произведения двух зависимых событий равна произведению вероятности наступления первого события на условную вероятность второго события при условии, что первое событие уже наступило:
Теорема наступления хотя бы одного из событий. Вероятность наступления хотя бы одного из событий А1, А2, …, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Следствие. Если события Аi имеют одинаковую вероятность появиться р, то вероятность появления хотя бы одного события из n независимых событий:
Формула волной вероятности. Пусть событие А может появиться вместе с одним из попарно несовместных событий
Условная вероятность наступления события Вi, при условии, что событие А произошло, определяется по формуле Байеса:
где
1 Производится три выстрела по мишени. Рассматриваются события: А1 – попадание в цель первым выстрелом; А2 – попадание в цель вторым выстрелом; А3 – попадание в цель третьим выстрелом. Определить, каким событиям равносильны следующие события: 1)
3) 7) 2 Монета подбрасывается три раза. Рассматриваются события Аi 3 Круговая мишень состоит из трех зон. Вероятности попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35 и 0,4. Найти вероятность: а) попадания в первую или третью зоны; б) промаха по мишени. 4 Вероятность поражения первой мишени для данного стрелка равна 0,6. Если при первом выстреле зафиксировано попадание, то стрелок получает право на следующий выстрел по второй мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,3. Определить вероятность поражения второй мишени. 5 В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из отобранных наудачу трех студентов: а) все три девушки; б) первые две девушки, третий - юноша; в) все три юноши? 6 Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производятся по одному до первого попадания. Определить вероятность того, что придется производить четвертый выстрел. 7 Вероятность безотказной работы автомобиля равна 0,9. Автомобиль перед выходом на линию осматривается двумя механиками. Вероятность того, что первый механик обнаружит неисправность, равна 0,8, а второй – 0,9. Если хотя бы один механик обнаружит неисправность, то автомобиль отправляется в ремонт. Найти вероятность того, что: а) автомобиль будет выпущен на линию; б) автомобиль не будет выпущен на линию. 8 Вероятность одного попадания в цель при одновременном залпе из двух орудий 0,38. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8. 9 Из 40 деталей в ящике 5 бракованных. Какова вероятность того, что взятые две детали не будут бракованными? 10 В коробке 12 карандашей трех цветов, по четыре карандаша каждого цвета. Наудачу последовательно вынимают три карандаша. Найти вероятность того, что все карандаши окажутся разного цвета. Решить задачу при условии: а) карандаши возвращают в коробку; б) карандаши не возвращают в коробку.
11 Из урны, содержащей четыре красных и шесть черных шаров, вынимают два шара (без возвращения первого). Какова вероятность того, что будут вынуты: а) оба шара черного цвета; б) красный и черный в любой последовательности; в) второй шар будет черным; г) оба шара одного цвета? 12 Вероятность выигрыша по лотерейному билету равна 0,1. Приобретено три билета. Какова вероятность выиграть хотя бы по одному из них? 13 Вероятность попадания в цель при стрельбе из орудия равна 0,6. Производится по одному выстрелу одновременно из трех орудий. Цель будет поражена, если в нее попадут не менее двух орудий. Найти вероятность: а) поражения цели; б) промаха одним или двумя орудиями. 14 Слово «машина» составлено из букв разрезной азбуки. Какова вероятность того, что перемешав буквы и укладывая их в ряд по одной, получим слово: а) «машина»; б) «шина»; в) «маша»? 15 В магазин вошли три покупателя. Вероятность того, что каждый что-нибудь купит, равна 0,3. Найти вероятность того, что: а) два из них совершат покупки; б) все три совершат покупки; в) ни один не совершит покупки; г) по крайней мере два совершат покупки; д) хотя бы один купит товар. 16 Вероятность получить высокие дивиденды по акциям на первом предприятии – 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии. 17 В продаже имеется 12 акций одного предприятия, 8 другого и 10 третьего. Клиент покупает три акции. Найти вероятность того, что клиентом будут куплены: а) акции одного предприятия; б) все три акции разных предприятий. 18 Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым появится шесть очков. Найти вероятность выигрыша для каждого игрока. 19 Через автобусную остановку проходят автобусы семи маршрутов с равной частотой. Пассажир ожидает автобус одного из маршрутов №1, №5, №7. Какова вероятность, что нужный ему автобус будет одним из первых трех подошедших к остановке? 20 Читатель в поисках нужной книги обходит три библиотеки. Вероятность того, что она имеется в очередной библиотеке равна 0,3. Что вероятнее – найдет читатель книгу или нет? 21 В денежно-вещевой лотерее на каждые 1000 билетов приходится 12 денежных и 8 вещевых выигрышей. Какова вероятность выигрыша хотя бы на один из трех приобретенных билетов? 22 В урне 10 красных, 5 зеленых и 3 черных шара. Определить вероятность того, что взятые наудачу два шара будут: а) одного цвета; б) разных цветов. 23 На базу поступило 40 ящиков овощей, из них 30 первого сорта. Наудачу для проверки берут два ящика. Какова вероятность, что оба содержат овощи: а) первого сорта; б) разного сорта; в) одного сорта? 24 Читатель разыскивает книгу в трех библиотеках. Одинаково вероятно, есть или нет в фонде очередной библиотеки книга и также одинаково вероятно, выдана она или нет. Чему равна вероятность того, что читатель найдет нужную книгу? 25 Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично» равна для первого студента 0,7, для второго - 0,6, для третьего – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»: а) одним студентом; б) двумя студентами; в) хотя бы одним; г) ни одним?
26 Первый студент из 20 вопросов программы выучил 17, второй – 12. Каждому студенту задают по одному вопросу. Определить вероятность того, что: а) оба студента правильно ответят на вопрос; б) хотя бы один ответит верно; в) правильно ответит только первый студент. 27 Сколько раз необходимо бросить игральную кость, чтобы с вероятностью 0,9 хотя бы один раз выпало не менее четырех очков? 28 В первой бригаде 6 тракторов, во второй – 9. В каждой бригаде один трактор требует ремонта. Из каждой бригады наудачу выбирают по одному трактору. Какова вероятность того, что: а) оба трактора исправны; б) один требует ремонта; в) трактор из второй бригады исправен. 29 На предприятии имеется три автомобиля. Вероятность безотказной работы первого из них равна 0,9, второго – 0,7, третьего – 0,8. Найти вероятности всех возможных значений числа автомобилей, работающих безотказно в течение определенного времени. 30 Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,784. Найти вероятность одного промаха при трех выстрелах. 31 В круг радиуса R вписан прямоугольник наибольшей площади. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся внутри заданного прямоугольника? 32 В шар радиуса R вписан прямой конус наибольшего объема. Чему равна вероятность того, что из поставленных наудачу внутри шара двух точек хотя бы одна окажется внутри конуса. 33 Вероятность спортсменом взять в одной попытке высоту 1,8 м равна 0,6, высоту 2 м – 0,2, высоту 2 м 10 см – 0,1. Спортсмен, не взявший предыдущую высоту, выбывает из соревнований. Спортсмену на каждую высоту дается три попытки. Определить вероятность того, что спортсмен закончит соревнования, взяв высоту: а) 1,8 м; б) 2 м; в) 2 м 10 см. 34 В первой урне 5 красных, 3 белых и 2 черных шара. Во второй 3 белых и 2 черных шара. Из первой урны взято 2 шара, а из второй один. Определить вероятность того, что среди них: а) все шары одного цвета; б) все шары разного цвета. 35 При исследовании жирности молока коров все стадо было разбито на три группы. В первой группе оказалось 70%, во второй 23% и в третьей 7% всех коров. Вероятность того, что молоко, полученное от отдельной коровы имеет не менее 4% жирности, для каждой группы коров соответственно равна 0,6; 0,4 и 0,1. Определить вероятность того, что для взятой наудачу коровы жирность молока составит не менее 4%. Взятая наудачу корова дает молоко жирностью не менее 4%. Найти вероятность того, что эта корова из первой группы. 36 В первой урне 10 деталей, из них 8 стандартных. Во второй 6 деталей, из которых 5 стандартных. Из второй урны переложили в первую одну деталь. Какова вероятность того, что деталь, извлеченная после этого из второй урны, нестандартная?
37 Имеются две урны. В первой – семь красных шаров и три черных, во второй – три красных и четыре черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным. 38 Торговая фирма получает однотипные товары от трех поставщиков. Объемы поставок товаров относятся как 1: 2: 3. Известно, что удельный иес товаров высокого качества от первого поставщика составляет 2/3, второго 3/4 и третьего 5/6. Найти вероятность того, что взятая случайно единица товара будет высокого качества. Если взятая единица товара высокого качества, то наиболее вероятно, от какого поставщика она поступила? 39 Предприятие использует для производства продукта сырье трех других предприятий. Объем поступающего сырья относится в пропорции 1: 2: 5. Известно, что первое предприятие поставляет 60 % сырья высокого качества, второе 70 % и третье 90 %. Случайно взятая единица сырья оказалась высокого качества. Найти вероятность того, что она поступила от второго или третьего предприятия. 40 В первом ящике из 20 деталей 4 бракованных, во втором из 30 деталей 5 бракованных. Из первого во второй переложили две детали. Найти вероятность того, что деталь, извлеченная после этого из второго ящика, бракованная. 41 Исследование рынка хлебобулочных изделий показало, что на долю фирмы А приходится 40 % объема реализации продукции, фирмы В – 32 % и фирмы С – 28 %. Известно, что на долю хлеба приходится 65 % реализованной продукции фирмы А, 40 % - фирмы В и 70 % - фирмы С. Определить долю каждой фирмы на рынке хлеба. 42 Для посева заготовлены семена 4 сортов пшеницы, из которых 20% семян 1-го сорта, 30% - 2-го сорта, 10% - 3-го сорта и 40% - 4-го сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 40 зерен, для первого сорта равна 0,5, для второго – 0,3, для третьего – 0,2, для четвертого – 0,1. Найти вероятность того, что наудачу взятое зерно даст колос, содержащий не менее 40 зерен. 43 Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно вызванный студент ответил на два заданных вопроса. Какова вероятность, что он из тех трех студентов, которые подготовили по 10 вопросов? 44 Запасная деталь может находиться в одной из трех партий с вероятностями p1 = 0,2; p2 = 0,5; p3 = 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8 и 0,7. Определить вероятность того, что: а) взятая наудачу деталь проработает положенное время; б) деталь, проработавшая положенное время, взята из второй или третьей партии. 45 Имеется 5 урн. В первой, второй и третьей находится по 4 белых и 6 черных шаров, в четвертой и пятой урнах по 2 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что была выбрана четвертая или пятая урна, если извлеченный шар оказался белым?
46 В первой бригаде производится в три раза больше продукции, чем во второй. Вероятность того, что производимая продукция окажется стандартной для первой бригады, равна 0,7, для второй – 0,8. Определить вероятность того, что взятая наугад единица продукции будет стандартной. Взятая наугад единица продукции оказалась стандартной. Какова вероятность, что она из второй бригады? 47 Покупатель с равной вероятностью посещает 3 магазина. Вероятность того, что он купит товар в первом магазине, равна 0,4, во втором - 0,3, в третьем - 0,2. Определить вероятность того, что покупатель купит товар только в одном магазине, если каждый магазин он посетил дважды.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 963; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.012 с.) |

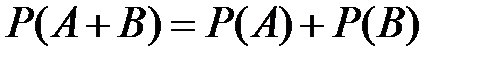 . (2.1)
. (2.1) . (2.2)
. (2.2)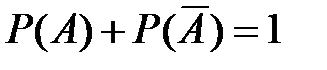 или p + q = 1. (2.3)
или p + q = 1. (2.3)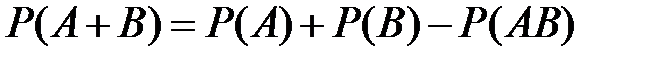 . (2.4)
. (2.4)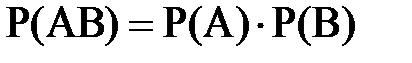 ;
;  . (2.5)
. (2.5) ; (2.6)
; (2.6)  . (2.7)
. (2.7)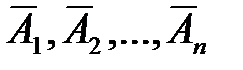 :
: . (2.8)
. (2.8)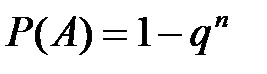 , где р + q = 1. (2.9)
, где р + q = 1. (2.9)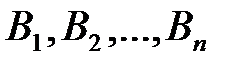 образующих полную группу событий. Будем называть события
образующих полную группу событий. Будем называть события  гипотезами для события А. Тогда вероятность наступления события А определяется по формуле:
гипотезами для события А. Тогда вероятность наступления события А определяется по формуле: , (2.10)
, (2.10) . (2.11)
. (2.11) , (2.12)
, (2.12) , (2.13)
, (2.13)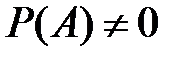 - находится по формуле полной вероятности.
- находится по формуле полной вероятности. ; 2)
; 2) 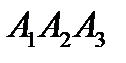 ;
; ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ;
; ; 8)
; 8)  ; 9)
; 9)  .
. – появление герба при
– появление герба при  – ом подбрасывании
– ом подбрасывании 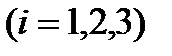 . Представить в виде сумм, произведений и сумм произведений событий Ai и
. Представить в виде сумм, произведений и сумм произведений событий Ai и 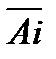 следующие события:
следующие события:  - появились все три герба;
- появились все три герба;  - появились все три цифры;
- появились все три цифры; 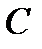 - появился хотя бы один герб;
- появился хотя бы один герб;  - появилась хотя бы одна цифра;
- появилась хотя бы одна цифра; 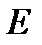 - появился только один герб;
- появился только один герб;  - появилась только одна цифра.
- появилась только одна цифра.


