
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерные случайные величиныСодержание книги
Поиск на нашем сайте На одном и том же пространстве элементарных исходов можно рассматривать не одну, а несколько случайных величин. Например, подбрасывают три игральных кубика. Можно рассматривать одну случайную величину ξ – сумма выпавших очков или три случайных величины: ξ1 – число выпавших очков на 1-ом кубике, ξ2 – число выпавших очков на 2-ом кубике, ξ3 – число выпавших очков на 3-ем кубике. В экономике, как правило, на показатель действует несколько факторов, например, качество продукции зависит от многих факторов. Пусть ξ1, ξ2, …, ξn –система случайных величин, определенных на множестве Функция распределения системы случайных величин определяется формулой F(x1, x2, …, xn) = P(ξ1 <x1, ξ2 <x2,..., ξn <xn), (20) где x1, x2, …, xn При этом F(x1, x2, …, xn) – неубывающая функция каждого аргумента. Для дискретной системы случайной величины закон распределения определяется заданием вектора x1, x2, …,xn и вектора вероятностей
таких, что Функция распределения выражается в виде кратной суммы F(x1, x2, …, xn) = где суммирование производится по всем возможным значениям каждой из случайных величин, для которых Система ξ1, ξ2, …, ξn называется непрерывной,если существует f(x1, x2, …, xn) F(x) можно представить в виде n-мерного интеграла F(x) = Функция f ( f( в точках непрерывности. случайные величины ξ1, ξ2, …, ξn называются независимыми, если для любых x1, x2, …, xnнезависимы события Для не зависимых ξ1, ξ2, …, ξn функция распределения равна произведению функций распределения каждой случайной величины F(x1, x2, …, xn) = Также справедливы равенства: для дискретных случайных величин Р = для непрерывных случайных величин f( Основными числовыми характеристиками n случайных величин являются математические ожидания М( и дисперсии D( Лекция 11. Условным законом распределения одной случайной величины,входящей в систему, называется закон, найденный при условии, что другая случайная величина, входящая в эту же систему, приняла определенное значение. Условный закон распределения задается как функцией распределения, так и плотностью распределения. Если рассматривается распределение случайной величины ξi при условии, что другая случайная величина ξj приняла определенное значение, то условная функция распределения обозначается F(x/y), а плотность – f(x/ y). Важными характеристиками являются условные математические ожидания и условные дисперсии. Пусть случайная величина ξi принимаетзначения a = ( Условным математическим ожиданием дискретнойслучайной величины ξi при ξj = bназывают сумму произведений возможных значений ξ i на их условные вероятности. Тогда условное математическое ожидание вычисляется по формуле: M(ξi / ξj=b) = Для непрерывных случайных величин M(ξi / ξj=b) = Особая роль в изучении системы случайных величин принадлежит корреляционному моменту (ковариации). Ковариацией случайных величин ξ i и ξj называется число
Для независимых случайных величин ковариация равна нулю т.к. в этом случае M(ξiξj) = M(ξi)M(ξj). Очевидно, что Все парные ковариации составляют симметричную относительно главной диагонали ковариационную матрицу размерностью (n
Определитель ковариационной матрицы является обобщенной дисперсией системы случайных величин.. Рассмотрим систему только двух случайных величин, пусть ξ1, ξ2. Пусть случайная величина ξ1 принимает значения из множества X, ξ2 – из множества Y, (X,Y) -действительные числа. Мерой линейной зависимости двух случайных величин ξ1, ξ2 является коэффициент корреляции
Свойства коэффициента корреляции: 1. |ρ| 2. |ρ|=1 тогда и только тогда, когда между случайными величинами существует линейная функциональная взаимосвязь y = аx + b, (29) где причем, если ρ= 1, то a > 0, если ρ= -1, то a < 0 (Рис. 15)
Рис. 15. Для независимых случайных величин ρ = 0, но обратное утверждение неверно, т.к. между случайными величинами может быть другой тип взаимосвязи (нелинейной).Чем ближе значение ρ к нулю, тем слабее линейная взаимосвязь, чем ближе по модулю к единице, тем -сильнее. Если ρ = 0, то говорят, что случайные величины некоррелированы. Можно показать, что если нормально распределенные случайные величины некоррелированы, то они и независимы. Пусть –1<ρ<1 и ρ≠0. Если нанести точки (X,Y) на координатную плоскость XoY, то можно заметить, что эти точки группируются вокруг некоторой прямой y = ax + b. Вычислим коэффициенты a,b этой прямой из условия, что дисперсия
. . . .
Рис. 16. Уравнение, относительно которого дисперсия минимальна, называется уравнением регрессии. Рассматривая дисперсию как функцию от двух переменных a и b воспользуемся необходимым условием экстремума
Решая эту систему относительно a и b, получим
при этом дисперсия Таким образом, уравнение регрессии у = Количественной характеристикой нелинейной взаимосвязи случайных величин ξ1, ξ2 является корреляционное отношение. Коэффициент корреляционного отношения ξ2 по ξ1 вычисляется по формуле:
где Свойства корреляционного отношения: 1. 2. η=0 соответствует некоррелированным случайным величинам. 3. η=1,тогда и только тогда, когда имеет место функциональная зависимость между ξ1 и ξ2. В случае линейной зависимости ξ2 от ξ1 корреляционное отношение совпадает с квадратом коэффициента корреляции. Корреляционное отношение несимметрично относительно ξ1 и ξ2, поэтому наряду с Теперь рассмотрим совокупность n-случайных величин
ρij=ρji, i≠j т.е. матрица симметрична относительно главной диагонали. Взаимосвязь какой-либо случайной величины ξi со всеми остальными случайными величинами характеризуется множественным коэффициентом корреляции
|R| - определитель матрицы R, Rjj – алгебраическое дополнение, соответствующее элементу корреляционной матрицы ρjj,
Лекция 12. Предельные теоремы.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 .
.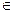 (
(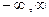 )
) ,
,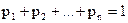 .
.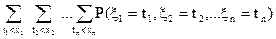 , (21)
, (21) .
. 0 такая, что для любых x1, x2, …, xnфункцию распределения
0 такая, что для любых x1, x2, …, xnфункцию распределения . (22)
. (22) ) называется плотностью распределения вероятностей системы случайных величин,
) называется плотностью распределения вероятностей системы случайных величин,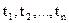 ) =
) =  (23)
(23) .
.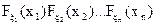 . (24)
. (24) =
=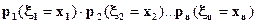 ,
,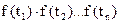 .
. ) =
) =  (25)
(25)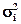 =
= 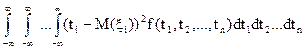 . (26)
. (26)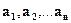 ), а случайная величина ξj - b = (
), а случайная величина ξj - b = ( ).
). . (27)
. (27) . (28)
. (28) = cov(ξiξj) = M((ξ i-M(ξ i))(ξ j-M(ξj)))=M(ξiξj)-M(ξi)M(ξj), i,j=1,2,…n.
= cov(ξiξj) = M((ξ i-M(ξ i))(ξ j-M(ξj)))=M(ξiξj)-M(ξi)M(ξj), i,j=1,2,…n. =
= 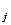 ξ
ξ  )
) n).
n). =
= 

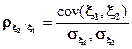 ,
,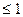 .
.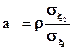
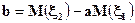 ,
,
 отклонений точек (X,Y) от точек на прямой была минимальна.
отклонений точек (X,Y) от точек на прямой была минимальна.
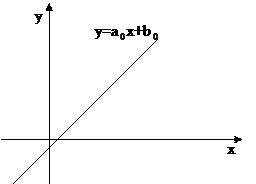 .
.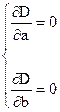
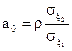 ,
,  , уравнение регрессии - у =
, уравнение регрессии - у =  (Рис.16),
(Рис.16), , и она является минимальной.
, и она является минимальной.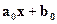 , дает наилучшее линейное представление ξ2 по ξ1.
, дает наилучшее линейное представление ξ2 по ξ1.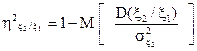 , (30)
, (30)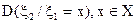 - условная дисперсия, характеризующая рассеяние ξ2 около условного математического ожидания
- условная дисперсия, характеризующая рассеяние ξ2 около условного математического ожидания 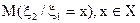 .
. .
. рассматривается
рассматривается  , определяемое аналогичным образом. Между
, определяемое аналогичным образом. Между 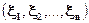 .Можно вычислить коэффициенты корреляции ρij между каждой парой случайных величин. Они составят корреляционную матрицу
.Можно вычислить коэффициенты корреляции ρij между каждой парой случайных величин. Они составят корреляционную матрицу
 (31)
(31)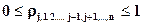 .
.


