Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность попадания непрерывной случайной величины на заданный участок числовой оси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Имеем участок числовой оси в пределах от Событие Событие Событие По теореме сложения вероятностей для
Оказывается, вероятность попадания случайной величины на заданный участок числовой оси равна приращению функции распределения на этом участке. Найдем теперь
Это есть не что иное как производная функции распределения. Обозначим ее Рассмотрим непрерывную случайную величину с плотностью распределения
Вероятность попадания случайной величины на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна
Геометрически это опять будет площадь.
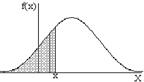
Как можно представить функцию распределения на этом графике? Сначала запишем формулу для функции распределения:
Геометрический смысл функции распределения - это площадь, ограниченная сверху графиком функции, а снизу - осью абсцисс, справа - вертикальным отрезком. Условие нормировки для непрерывной случайной величины. Чему равна вероятность попасть на любой участок числовой оси.? То есть при нахождении такой вероятности мы должны взять интеграл в пределах от -µ до +µ. А геометрически это будет площадь под всей кривой.
Числовые характеристики непрерывной случайной величины. Математическое ожидание. Не останавливаясь подробно на выводе этой формулы, отметим лишь, что ее легко получить из формулы для математического ожидания дискретной случайной величины, произведя соответствующие замены. От суммирования дискретных значений переходим к интегрированию на отрезке числовой оси. Соответственно суммирование по всем возможным значениям заменяется на интегрирование в пределах
Дисперсия непрерывной случайной величины. Аналогичные преобразования дают возможность получит формулу для дисперсии непрерывной случайной величины.
Средне-квадратичное отклонение (стандартное отклонение)
Основные законы распределения случайных величин. Законы распределения дискретной случайной величины. Биномиальное распределение. Пусть производится
где Число сочетаний вычисляется по формуле: причем Таблица биномиального распределения имеет вид:
Числа Пример 1. Вероятность рождения мальчика равна 0,515. Как велика вероятность того, что из 10 наугад выбранных новорожденных будет 6 мальчиков? Предположение о независимости может считаться выполненным. Следовательно, для искомой вероятности имеем
Пример 2. Появление колонии микроорганизмов данного вида в определенных условиях оценивается вероятностью 0,7. Найти вероятность того, что в шести пробах данная колония микроорганизмов появится 4 раза. Решение. Распределение Пуассона. Случайная величина называется распределенной по закону Пуассона, если она принимает счетное множество возможных значений 0, 1, 2... с вероятностями, которые вычисляются по формуле:
Следует отметить, что из всех дискретных распределений, распределение Пуассона встречается чаще других. Оно тесно связано с биномиальным распределением, являясь предельным.
Если в биномиальном распределении зафиксировать
Распределение Пуассона затабулировано для различных значений параметра Пример 1. Известно, что в среднем на приеме у врача бывает ежедневно 5 пациентов. Найти вероятности обслуживания в день от 0 до 12 пациентов. Решение:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.207 (0.01 с.) |


 до
до 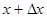 . Рассмотрим отдельно три события?
. Рассмотрим отдельно три события?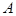 , которое состоит в том, что
, которое состоит в том, что  .
.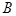 , которое состоит в том, что
, которое состоит в том, что  .
.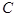 , которое состоит в том, что
, которое состоит в том, что 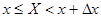 .
. получаем:
получаем: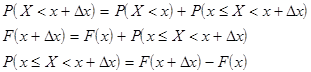
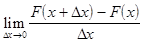 .
.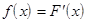 и назовем плотностью распределения. Плотность распределения, так же как и функция распределения, есть одна из форм задания закона распределения для непрерывной случайной величины. В противоположность функции распределения, эта форма не является универсальной, она существует только для непрерывной случайной величины.
и назовем плотностью распределения. Плотность распределения, так же как и функция распределения, есть одна из форм задания закона распределения для непрерывной случайной величины. В противоположность функции распределения, эта форма не является универсальной, она существует только для непрерывной случайной величины.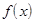 и элементарный участок, примыкающий к точке
и элементарный участок, примыкающий к точке 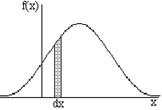
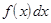 . Эту величину
. Эту величину 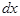 .Если увеличить область на числовой оси до некоторого интервала
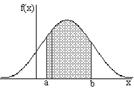
.Если увеличить область на числовой оси до некоторого интервала  , то вероятность попадания на этот отрезок будет равна сумме элементов вероятности на всем участке, то есть интегралу
, то вероятность попадания на этот отрезок будет равна сумме элементов вероятности на всем участке, то есть интегралу .
.
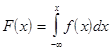 .
.
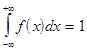 .
.
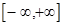 . Вероятность отдельного значения дискретной случайной величины
. Вероятность отдельного значения дискретной случайной величины 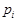 заменим на элемент вероятности для непрерывной случайной величины
заменим на элемент вероятности для непрерывной случайной величины 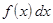 . Тогда получаем:
. Тогда получаем: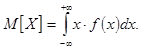

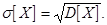
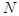 независимых опытов. В каждом опыте с одной и той же вероятностью
независимых опытов. В каждом опыте с одной и той же вероятностью 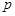 может наступить событие
может наступить событие  - это число
- это число 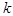 наступлений события
наступлений события  вычисляются по формуле:
вычисляются по формуле: ,
, .
.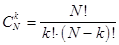 ,
,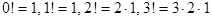 и т. д.
и т. д.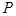

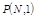
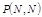
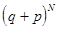 . Отсюда и распределение получило такое название.
. Отсюда и распределение получило такое название.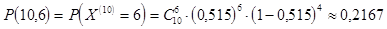 .
.
 ,
,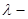 параметр распределения.
параметр распределения.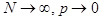 , таким образом, чтобы произведение
, таким образом, чтобы произведение  оставалось постоянным и равным
оставалось постоянным и равным 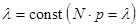 , то получим
, то получим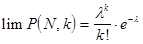 .
. .
.