
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики функций многих переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть Y = j(x1, x2,…xn), где Х1, Х2,…Хn - случайные величины с известной совместной n-мерной плотностью вероятностей Начальные моменты:
Центральные моменты:
Основные числовые характеристики: Ø Математическое ожидание функции от произвольного числа случайных аргументов. Для непрерывных величин:
где
Ø Дисперсия функции от произвольного числа аргументов для непрерывных случайных величин
или аналогичная форма
На практике редко известна совместная плотность вероятности; известны лишь числовые характеристики. Определение числовых характеристик функций по заданным числовым характеристикам аргументам значительно упрощает решение задач теории вероятностей. Чаще всего такие упрощенные функции относятся к линейным функциям, однако некоторые элементарные нелинейные функции также подразумевают подобный подход. Пусть известны векторы М [ хi ] = mi D [ хi ]= Di системы случайных величин (Х1, Х2,…Хn) - с известной совместной n-мерной плотностью вероятностей Задача определения числовых характеристик Y в таком случае разрешима только для определения классов функций j.
Характеристические функции и моменты Характеристические функции До сих пор мы задавали случайные величины законом распределения. Характеристическая функция - ещё один способ представления случайных величин. Пусть X - случайная величина. Её характеристической функцией w (t) назовём математическое ожидание случайной величины eitX: w(t)= MeitX, где под комплексной случайной величиной eitX мы понимаем комплексное число eit X =cos(tX) + i sin(tX), а M (eitX)= M [cos(tX)+ iM[ sin(tX)]; независимая переменная t имеет размерность X -1. Характеристическая функция - преобразование Фурье-Стилтьеса функции распределения:
В непрерывном случае w (t) - преобразование Фурье плотности вероятности:
Если w (t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность f (x) по характеристической функции:
В дискретном случае:
Особо отметим дискретные случайные величины с целочисленными значениями, например, при xk = k:
здесь w (t) - ряд Фурье в комплексной форме, вероятности pk играют роль коэффициентов Фурье и легко восстанавливаются по f (t):
В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.
Свойства характеристических функций
Важнейшим свойством характеристической функции, сделавшим её одним из главных инструментов современной теории вероятностей, оказалось то, что при суммировании независимых случайных величин их характеристические функции перемножаются: если X и Y независимы, то для случайной величины Z = X + Y: wZ (t)= wX (t)× wY (t). Действительно, wZ (t)= M (eitZ)= M (eit ( X + Y ))= M (eitX × eitY)= M (eitX)× M (eitY)= wX (t)× wY (t). Законы распределения при суммировании независимых слагаемых ведут себя гораздо сложнее (см. Л12, закон распределения суммы случайных величин). Если Y = aX + b, то wY (t)= M (eit (aX + b ))= eitb × M (eitaX)= eitb × wX (at). Другим важным свойством характеристических функций является их простая связь с моментами. Предполагая возможность дифференцирования под знаком математического ожидания в равенстве w (t)= MeitX, получим: w (k)(t)= ikM (Xk × eitX). При t =0:
Таким образом, характеристическая функция позволяет заменить интегрирование при вычислении моментов дифференцированием. В частности,
Характеристическую функцию определяют также и для n -мерной случайной величины (X 1, X 2,, ¼, Xn): w (t 1, t 2,, ¼, tn)= M (exp i (t 1 X 1+ t 2 X 2+¼+ tnXn)). Примеры применения характеристических функций 14.3.1.. Биноминальное распределение. Пусть дискретная случайная величина имеет биноминальное распределение X:B (n, p).
Дифференцирование даёт:
14.3.2. Пуассоновское распределение. Пусть дискретная случайная величина имеет пуассоновское распределение X:P(l).
Отсюда сразу найдём: M [ X ]=l, D[ X ]=l. 14.3.3. Экспоненциальный закон распределения. Пусть непрерывная случайная величина имеет экспоненциальное распределение X:Exp(m).
Из этого равенства следует:
14.4. Нормальный закон распределения. Пусть непрерывная случайная величина имеет нормальное распределение X:N(0, 1).
Примем во внимание, что eitx =cos(tx) + i sin(tx):
Второй из этих интегралов равен нулю, так как его подынтегральная функция нечётна. Ввиду чётности подынтегральной функции первого интеграла:
Обозначим:
Очевидно,
интегрируем по частям:
Таким образом, J’ (t)=- tJ (t), и J (0)= Решение этого дифференциального уравнения дает:
Окончательно: w (t)= Тогда для нормально распределенной случайной величины X:N(a, s): и сразу же находим: M[ X ]= a, D[ X ]=s2. По поводу характеристической функции нормального закона можно заметить интересное его свойство: сумма независимых нормально распределённых случайных величин распределена по нормальному закону. Действительно. Пусть X и Y независимые случайные величины, причём, X: N (a 1, s1), Y:N (a 2, s2), а Z = X + Y. Характеристические функции X и Y: wX (t)= Для характеристической функции Z имеем: wZ (t)= wX (t)× wY (t)=exp[ i (a 1+ a 2) t - но это означает, что Аналогичным свойством обладают и независимые пуассоновские случайные величины: сумма независимых случайных величин, распределённых по закону Пуассона, распределена по закону Пуассона. В самом деле, если X: P(l1), X: P(l2), то wX (t)=exp[l1(eit -1)], wY (t)=exp[l2(eit -1)], поэтому характеристическая функция случайной величины Z = X + Y: wZ (t)= wX (t)× wY (t)=exp[(l1+l2)(eit -1)], но это значит, что Z: P(l1+l2). Законы, сохраняющиеся при сложении независимых случайных величин, называются безгранично делимыми. Нормальный и пуассоновский - примеры таких законов.
ЗАКОН БОЛЬШИХ ЧИСЕЛ Пусть проводится опыт Е, в котором нас интересует признак Х, или СВ Х. При однократном проведении Е нельзя заранее сказать, какое значение примет Х. Но при n -кратном повторении «среднее» значение величины Х (среднее арифметическое) теряет случайный характер и становится близким к некоторой константе. Закон больших чисел – совокупность теорем, определяющих условия стремления средних арифметических значений случайных величин к некоторой константе, при увеличении числа опытов до бесконечности (n®¥).
НЕРАВЕНСТВА ЧЕБЫШЕВА Теорема. Для любой случайной величины X с mx, Dx выполняется следующее неравенство Доказательство: 1. Пусть величина Х – ДСВ. Изобразим значения Х и Мх в виде точек на числовой оси Ох
0 х1 А Мх В Вычислим вероятность того, что при некотором
Это событие заключается в том, что точка Х не попадет на отрезок [ mx-ε, mx+ε ], т.е.
для тех значений x, которые лежат вне отрезка [ mx-ε, mx+ε ]. Рассмотрим дисперсию с.в. Х:
Т.к. все слагаемые – положительные числа, то если убрать слагаемые, соответствующую отрезку [ mx-ε, mx+ε ], то можно записать:
т.к.
Þ 2. Для НСВ:
Применяя неравенство
Откуда и вытекает неравенство Чебышева для НСВ. Следствие. Доказательство: События ================================================================================== 1. Лемма: Пусть Х –СВ, e>0 – любое число. Тогда
Доказательство:
Т.к. Следствие. Д-во: Полагаем, вместо св Х – св Х-М(Х), т.к. М(Х-М(Х))2=D(X) и получаем неp-во. Следствие: (правило трех сигм для произвольного распределения): Полагаем в неравенстве Чебышева
Т.е. вероятность того, что отклонение св от ее МО выйдет за пределы трех СКО, не больше 1/9. Неравенствово Чебышева дает только верхнюю границ вероятности данного отклонения. Выше этой границы - значение не может быть ни при никаком распределении. СХОДИМОСТЬ ПО ВЕРОЯТНОСТИ
Последовательность случайных величин Xnсходится по вероятности к величине a,
где e,d - произвольно малые положительные числа. Одна из важнейших, но наиболее важных форм закона больших чисел – теорема Чебышева – она устанавливает связь между средним арифметическим наблюденных значений СВ и ее МО.
ТЕОРЕМА ЧЕБЫШЕВА Первая теорема Чебышева. При достаточно большом числе независимых опытов среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию:
Доказательство: Рассмотрим величину У равную
Определим числовые характеристики Yn my и DY.
Запишем неравенство Чебышева для величины Yn
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство
Переходя к противоположному событию:
Т.е. вероятность может быть сколь угодно близкой к 1. Вторая теорема Чебышева: Если Х1.....Хn – последовательность попарно независимых СВ с МО mx1....mxn и дисперсиями Dx1..Dxn ограничены одним и тем же числом Dxi<L (i=1..n), L=const, тогда для любого e, d> 0 – бесконечно малых
Доказательство: Рассмотрим СВ
Применим к Y неравенство Чебышева:
Заменим:
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство Т.е., взяв предел при n®¥ от обеих частей и
(так как вероятность не может быть больше 1).
Пример. Производится большое число n независимых опытов, в каждом из которых некоторая случайная величина имеет равномерное распределение на участке [1,2]. Рассматривается среднее арифметическое наблюденных значений случайной величины X. На основании Закона больших чисел выяснить, к какому числу а будет приближаться величина Y при n→∞. Оценить максимальную практически возможную ошибку равенства Y≈a. Решение.
Максимальное практически возможное значение ошибки ТЕОРЕМА БЕРНУЛЛИ
Пусть произведены n независимых опытов, в каждом из которых возможно событие А с вероятностью р. Тогда относительная частота появления события А в n опытах стремится по вероятности к вероятности появления А в одном опыте. Теорема Бернулли: При неограниченном увеличении числа опытов до n частота события А сходится по вероятности к его вероятности р: где
Событие Хi – число появлений события А в i-м опыте. СВ X может принимать только два значения: X=1 (событие наступило) и X=0 (событие не наступило). Пусть СВ Хi – индикатор события А в i-м опыте. Числовые характеристики хi: m i = p Di = pq. Они независимы, следовательно, можем применить теорему Чебышева:
Дробь
Пояснения: В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.011 с.) |

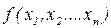 .
.

 ,
, - плотность распределения системы
- плотность распределения системы  .
.

 .
.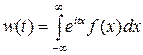
 .
. .
.
 .
.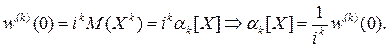

 .
. .
. .
. .
.


 .
. .
. ;
;
 .
.
 .
.
 , wY (t)=
, wY (t)=  .
. t 2],
t 2],
 где e>0.
где e>0.
 величина Х отклонится от своего МО не меньше чем на ε:
величина Х отклонится от своего МО не меньше чем на ε: .
. --
-- .
. ,
, , то неравенство можно усилить
, то неравенство можно усилить
 Þ
Þ 

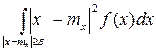 - это интегрирование по внешней части отрезка [ mx-ε, mx+ε ].
- это интегрирование по внешней части отрезка [ mx-ε, mx+ε ].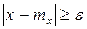 и подставляя его под знак интеграла, получаем
и подставляя его под знак интеграла, получаем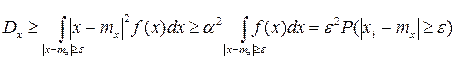 .
. - это 2-е неравенство Чебышева.
- это 2-е неравенство Чебышева. и
и  .
.
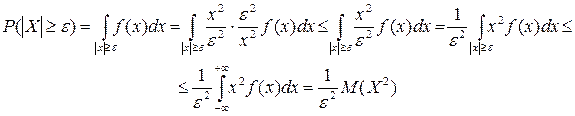 ,
, .
.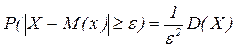 .
. , имеем
, имеем .
.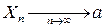 если при увеличении n вероятность того, что Xn и a будут сколь угодно близки, неограниченно приближается к единице:
если при увеличении n вероятность того, что Xn и a будут сколь угодно близки, неограниченно приближается к единице:

 .
.

 , где
, где  - сколь угодно малое число. Тогда
- сколь угодно малое число. Тогда .
.
 или
или 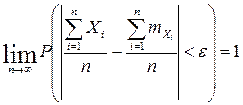
 .
. или
или 

 получаем:
получаем: .
.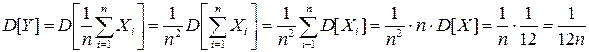 .
. .
.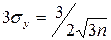 .
.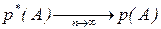 ,
, -- частота события А в n опытах, где m -число опытов в которых произошло событие А, n -число проведенных опытов или
-- частота события А в n опытах, где m -число опытов в которых произошло событие А, n -число проведенных опытов или или
или  .
.


 равна относительной частоте появлений события А в испытаниях Þ получаем
равна относительной частоте появлений события А в испытаниях Þ получаем .
.


