
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее понятие математического ожиданияСодержание книги
Поиск на нашем сайте
Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F (x): Y =φ(X). Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:
Определяем вероятности появления различных значений случайной величины У
Тогда математическое ожидание случайной величины Y определяется так:
Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности pi элементом вероятности f(x)dx, а сумму – интегралом, получаем:
Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидание, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента. Например, дисперсия случайной величины Y=φ(x) определяется так:
Величину M [ φ (x)] рассчитываем в соответствии с (9.1)-(9.3). Для определения математического ожидания квадрата φ (х) воспользуемся следующими соотношениями:
Таким образом, для нахождения числовых характеристик функции Y = φ (x) достаточно знать закон распределения ее аргумента. 9.2. Закон распределения функции дискретного случайного аргумента Для дискретной случайной величины Y = φ (х) определяем вероятности появления различных значений случайной величины:
Преобразуем полученную таблицу в ряд распределения случайной величины Y. Для этого расположим значения Y в порядке возрастания, а для определения вероятностей p{ Y = yi } будем руководствоваться следующими правилами: · если различным возможным значениям аргумента Х соответствуют различные возможные значения Y, то P { Y = φ (xi)}= pi; · если различным возможным значениям случайной величины Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений СВ Y. Полученный таким образом ряд является рядом распределения случайной величины Y. 9.3. Закон распределения функции непрерывного случайного аргумента Пусть Х – непрерывная случайная величина с известной плотностью вероятности. Алгоритм определения закона распределения СВ Y зависит от вида функции Y = j (х).
9.3.1. Р ассмотрим случай монотонного возрастания функции Y=φ(x) на интервале [a,b) определения случайной величины Х (рис. 9.1). Определим функцию распределения величины У:
Функция распределения случайной величины Y имеет вид:
Дифференцируя интеграл по переменной у, входящей в верхний предел, получим:
9.3.2. Рассмотрим случай, когда y=φ(х) монотонно убывающая функция на интервале [a,b) определения случайной величины Х (рис. 9.2).
Функция распределения СВ Y=φ(х) для СВ X, распределенной в интервале [ a,b], равна:
Плотность вероятностей для любого монотонного случая принимает вид:
9.3.3. Рассмотрим случай когда функция y=φ(x) на участке [ a, b) возможных значений случайной величины Х не монотонна (рис. 9.3).
Плотность вероятностей случайной величины Y равна
где: k – интервалов монотонности функции φ(x); ymin, ymax – соответственно минимальное и максимальное значение случайной величины Y; ymini, ymaxi – соответственно минимальное и максимальное значение случайной величины Y на i-ом интервале монотонности.
Пример 9.1. Определить плотность вероятности величины Y = X 2, если X - случайная величина, равномерно распределенная на интервале (-1, 2). Решение. В зависимости от числа k обратных функций выделим следующие интервалы для Y (см. рис. 3.1): (-, 0) k = 0, (0, 1) k = 2, (1, 4) k = 1, (4, +) k = 0.
Так как на интервалах (-, 0) и (4, +) обратная функция не существует, то g (y)=0. В интервале (0,1) две обратных функции: 1(y) = +
В интервале (1,4) одна обратная функция 1(y) = +
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.80.73 (0.008 с.) |

 (9.1)
(9.1)
 . (9.2)
. (9.2) (9.3)
(9.3)
 . (9.4)
. (9.4)
 Чтобы выполнилось условие
Чтобы выполнилось условие  , необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от а до х=ψ(х), где ψ(х) – функция, обратная функции j (x).
, необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от а до х=ψ(х), где ψ(х) – функция, обратная функции j (x).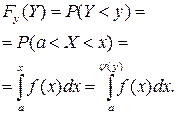

 .
. Функция распределения случайной величины Y определиться так:
Функция распределения случайной величины Y определиться так:

 (9.5)
(9.5) Число значений обратной функции ψ(y) зависит от того, какое значение Y выбрано. Событие Y<y равносильно попаданию случайной величины X в один из непересекающихся отрезков, отмеченных жирной линией на рис.9.3, где соответствующая часть кривой y-φ(X) лежит ниже прямой у. Попадания точки Х в эти отрезки – события несовместные; по правилу сложения вероятностей
Число значений обратной функции ψ(y) зависит от того, какое значение Y выбрано. Событие Y<y равносильно попаданию случайной величины X в один из непересекающихся отрезков, отмеченных жирной линией на рис.9.3, где соответствующая часть кривой y-φ(X) лежит ниже прямой у. Попадания точки Х в эти отрезки – события несовместные; по правилу сложения вероятностей (9.6)
(9.6) (9.7)
(9.7) Рис. 9.4
Рис. 9.4
 и 2(y) = -
и 2(y) = - 




